Основная теорема зубчатого зацепления. Понятия о линии и полюсе зацепления. Профилирование зубьев

Для обеспечения нормальной работы пары зубчатых колес с постоянным передаточным числом профили зубьев должны быть очерчены по кривым, подчиняющимся определенным законам. Эти законы вытека­ют из основной теоремы зацепления, сущность которой заключается в следующем.

Пусть имеется пара зубчатых колес с центрами О₁и О₂,вращающихся соответственно с угловыми скоростями и . На рис.18, а показаны сложения, которые последовательно занимает пара сопряженных (эвольвентных) зубьев в процессе их зацепления; прямую О₁О₂называют межосевой линией зубчатой передачи. Проведем в точках касания зубьев К₁, К₂, К₃, ... общие нормали к профилям. Все эти нормали NN должны пересекать межосевую линию О₁О₂в постоянной точке Р. Эту точку называют полюсом зацепления; ее положение на межосевой линии определяется отношением уг­ловых скоростей колес, т. е. их отношением:

.

а)б)

Рис. 18. Элементы зубчатого зацепления

Основную теорему зацепления можно сформулировать так: общая нор­маль к профилям зубьев в точке их касания пересекает межосевую линию в точке Р, называемой полюсом зацепления и делящей межосевое расстояние на отрезки, обратно пропорционально угловым скоростям.

Следствие: для обеспечения постоянного передаточного отношения по­ложение полюса Р на линии центров должно быть постоянным.

В процессе работы сопряженных (эвольвентных) профилей точка их касания все время перемещается по прямой NN. Эту прямую называют линией зацепления.

Место (точку) входа в зацепление и выхода из него сопряженных зубь­ев можно определить при следующем геометрическом построении.

Возьмем произвольное межосевое расстояние О₁О₂(рис.18, г) и раз­делим его в произвольном отношении . Радиусами О₂Р и O₁P проведем начальные окружности зубчатых колес через точку Р,касатель­ную ТТ кэтим окружностям и линию NN — нормаль к боковым поверхно­стям зубьев — под углом 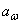и касательной ТТ. Угол 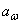называют углом за­цепления; в СНГ 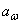принят 20°.

Примем произвольную высоту головки зубьев и проведем радиусами, равными и ,окружности выступов зубчатых колес (высота го­ловки зуба шестерни и колеса должна быть одинаковой). При направлении вращения колес, указанном на рисунке, зубья войдут в зацепление в точке А (точке пересечения нормали с окружностью выступов колеса) и выйду: из зацепления в точке В (точке пересечения нормали с окружностью вы­ступов шестерни).

Все точки касания сопряженных зубьев будут лежать на участке АВ ли­нии зацепления. Участок АВ называется рабочим участком линии зацепле­ния.

Необходимое условие непрерывности зацепления: дуга зацепления должна быть больше шага. В противном случае при выходе из зацепления одной пары зубьев вторая пара еще не войдет.

Длина линии зацепления q_a — отрезок линии зацепления, отсекаемый окружностями вершин зубьев сопряженных колес. Он определяет начало иконец зацепления пары сопряженных зубьев. Длина зацепления — актив­ная часть линии зацепления.

Коэффициент торцового перекрытия — отношение длины линии за­цепления к шагу:

.

Рис. 19. Геометрические параметры зубчатой передачи

Полюс зацепления Р (см. рис. 18, б) сохраняет неизменное положе­ние на линии центров О₁О₂. Следовательно, радиусы О₁P (r₁) и О₁P (r₁) также неизменны. Окружности радиусов r₁ и r₂называют начальными (делитель­ными). При вращении зубчатых колес эти окружности пе­рекатываются одна по другой без скольжения, о чем свидетельствует ра­венство их окружных скоростей (см. доказательство основной теоремы зацепления). Теоретически боковые поверхности зубьев (профи­ли) могут быть очерчены любыми кривыми, удовлетворяющими основному закону зубчатого зацепления. Такие профили называют сопряженными.

В современном машиностроении для построения сопряженных профилей применяют ограниченное число кривых.

Профили зубьев должны быть технологичными, т.е. такими, чтобы их можно было получить в производственных условиях наиболее простыми методами. Из теоретически возможных профилей преимущественное применение получили эвольвентные профили (см. рис. 18, б), так как такие про­фили проще обработать и они обладают большими преимуществами. Эвольвентное зацепление предложено Эйлером более 200 лет назад. Это зацепление по сравнению с другими имеет следующие преимущества: при изменении межосевого расстояния не нарушается правильность их зацепления (не изменяется передаточное число); это зацепление может быть использовано и в сменных колесах.

В зацеплении М.Л. Новикова рабочие профили зубьев очерчены дуга­ми окружностей (рис. 20, 21). По сравнению с эвольвентными передачами зацепления Новикова могут при одних и тех же габаритных размерах передавать в 1,5-2 раза большую мощность. Ввиду сложности изготовления и монтажа передачи с зацеплением Новикова пока нашли применение только в специальном машиностроении.

Рис. 20. Колесо с зацеплением М. Л. Новикова

Рис. 21. Кинематика зацепления зубчатых колес

Рис.22