Метод Эйлера. Пусть дано дифференциальное уравнение (I), с на­чальными условиями y(

Пусть дано дифференциальное уравнение 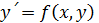(I), с на­чальными условиями y(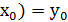

Пусть y=y(x) искомое точное решение. Интегральная кривая проходит через точку (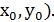

Найдем приближенные значения функции в точках 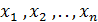. Построим систему равноотстоящих точек узлов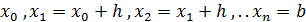

Проведем прямые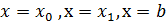

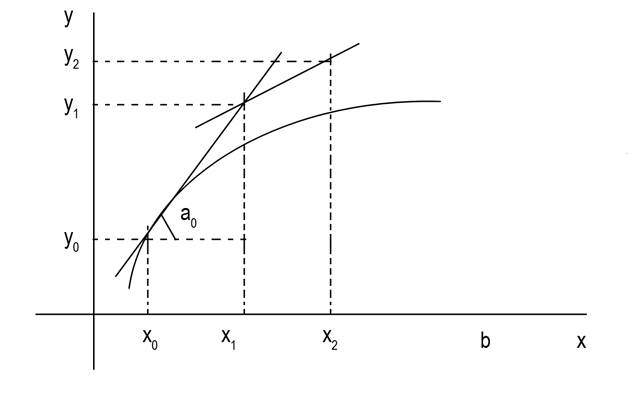
Рассмотрим отрезок [ ]

На этом отрезке есть одна точка, которая принадлежат искомой кри­вой - это точка А 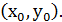Заме­ним дугу искомой кривой y=y(x) на отрезке [ ] касательной к ней, проведенной в точке ( )

В качестве 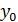возьмем ординату точки пересечения прямой x= 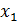с касательной.

Очевид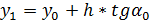но . Но ,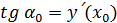

т.е. .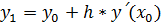

Но из уравнения (I) следует, чтo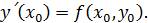

Итак, получаем .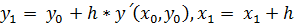

Предположим теперь, что точка 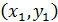принадлежит искомой кривой. В этой точке опять проведем касательную к графику функции до пересечения с прямой х = .

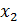Тогда аналогично:

.

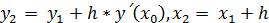Продолжая и так далее, получим систему значений 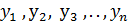которые и будут приближенными значениями функции y=y(x) в точках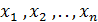

Итак, расчетные формулы метода Зилера:

.

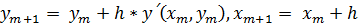Для системы дифференциальных уравнений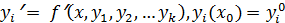

i= I,…,k

расчетные формулы записываются аналогично

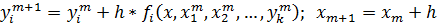
здесь i - номер уравнения в системе, n - номер шага.

Метод Эйлера является грубым методом, ошибка, которую мы допус каем ка каждом шаге пропорциональна 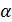, т.е. .

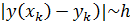Чтобы повысить точность вычислений, использует некоторые усовершенствованные методы.