Метод Эйлера-Коши

Пусть опять решаем уравнение y’=f(x,y), y(

Решение ищем на отрезке [ ].

Пусть нам известны координаты некоторой точки, принадлежащей ис­комому решению ( ). Найдем средний тангенс угла наклона ка­сательной для двух точек : ( ) и ( ).

Последняя точка, есть та самая, которую в методе Эйлера мы обоз­начаем ( ), но здесь точка будет вспомогательной.

Итак, сначала по методу Эйлера находится точка А, лежащая на прямой , тангенс угла накло­на которой

В этой точке снова вычисляется тангенс угла наклона касательной

Затем через точку ( ) проводим прямую L, тангенс уг­ла наклона которой равен

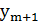Точка, в которой L пересе­чется с прямой ,будет искомой( ). Таким обра­зом, есть искомое приближение значения функции на данном шаге интегрирования.

Расчетные формулы метода Эйлера-Коша следующие:

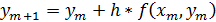
Аналогично, для системы дифференциальных уравнений:

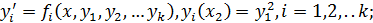
Здесь i - номер уравнения системы, m - номер шага.