К расчетно-графической работе

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

по дисциплине «Методы оптимизации в электроснабжении»

Направление подготовки бакалавров техники и технологии: 140600 – Электротехника, электромеханика и электротехнологии

Специальность подготовки: 140610 – Электрооборудование

и электрохозяйства предприятий, организаций и учреждений

Специализация подготовки 14061005

Электрооборудование и электроснабжение малых предприятий и быта

Форма обучения – очная

Тула 2007

Разработали:

проф. В.И. Ловчаков

асс. С.А. Шопин

Задача 1.Задача безусловной оптимизации

Определить все точки экстремума целевой функции. Найти глобальный минимум и максимум.

1. Найти частные производные функции f(x₁,x₂)

2. Определить стационарные точки

3. Найти вторые частные производные функции f(x₁,x₂) и составить матрицу Гессе

4. Рассчитать гессиан для каждой стационарной точки, определить характер экстремума по критерию Сильвестра

5. Определить точки глобального минимума и максимума

6. Построить график функции , демонстрирующий глобальный экстремум

Задача 2. Задача условной оптимизации.

Найти экстремум функции при наличии ограничений, заданных функцией , методом множителей Лагранжа.

1. Составить функцию Лагранжа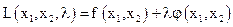

2. Найти частные производные функции Лагранжа

3. Определить стационарные точки

4. Найти вторые частные производные функции Лагранжа и составить матрицу Гессе

5. Рассчитать гессиан для каждой стационарной точки, определить характер экстремума по критерию Сильвестра

6. Построить графикb функции и и ограничивающей, демонстрирующий глобальный экстремум

7. Решить задачу встроенными средствами MathCAD

Задача 3. Численные методы одномерной оптимизации (минимизации)

Исходные данные: целевая функция f(x), отрезок [a;b], точность Δ.

1. Построить график функции на заданном отрезке

2. Составить программу в MathCAD, реализующую заданный метод одномерной оптимизации (минимизации функции).

3. Решить задачу встроенными средствами MathCAD