Краткие сведения о численных методах одномерной оптимизации

Метод полного перебора

Идея данного метода предельно проста и состоит в последовательном переборе значений заданной функции при всех значениях аргумента на данном отрезке, равностоящих друг от друга на некоторый шагDx.

Алгоритм поиска экстремума выглядит следующим образом:

1) отрезок [a,b] разбивают на n равных отрезков длиной Dx, т.е. .

2) определяют значения функции f(x) на границах отрезков в точках .

3) из множества значений функции f(x) в дискретных точках, т.е. находят минимальное значение

, тогда

Следующие два метода используют стратегию двух точек для сокращения интервала неопределенности.

Метод половинного деления

На исходном отрезке выбираются две точки в его середине по возможности ближе друг к другу: и . После проведения первой пары экспериментов в этих точках, сравнивая знаки функции получаем новый интервал неопределенности:

а) в случае задачи минимизации функции

, если

, если

б) в случае задачи максимизации функции

, если

, если

Снова разделим его пополам и выберем точки эксперимента вблизи середины, продолжая итерационный процесс.

Алгоритм:

1. Задать величину ε

2. Положить

3. Вычислить координаты точек x₁ и x₂:

,

4. Вычислить значения функции в точках x₁ и x₂: и

5. Если , то ,

если , то .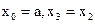

6. Если , то идем на шаг 3

7. Если , то

Метод золотого сечения

В отличие от метода половинного деления, в котором на каждом шаге вычисляется 2 новых значения функции в методе золотого сечения используется тот факт, что новый интервал неопределенности уже содержит одну точку с вычисленным значением.

На первом шаге точку x₂ на отрезке выбирают такой, чтобы исходный отрезок делился в соотношении называемом «золотым сечением»:

,

Можно показать, что – число Фидия.

Тогда , . Точка x₁ выбирается симметричной точке x₂ относительно середины отрезка, т.е. расстоянии 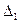от точки b, т.е.

Т.к. по результатам сравнения знаков функции выбирается один из двух отрезков длиной 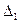, то в данном отношение длин интервалов неопределенности на соседних шагах остается постоянным:

.

Алгоритм:

1. Положить

2. Если , то – точка минимума.

Если , то идем на шаг 3

3. Рассчитываем координаты точек x₁ и x₂: ,

4. Вычислить значения функции в точках x₁ и x₂: и

5.

6. Если , то ,

если , то .

7.

8. Идем на шаг 2

Где i – номер шага.

Метод Фибоначчи

Процедура поиска аналогична методу золотого сечения. Применяется, когда треубется получить наилучшее приближение экстремума за заданное число шагов.

Отличие метода заключается в способе выбора начальной точки x₂. Ее положение выбирается такой, чтобы последовательность длин интервалов неопределенности удовлетворяла уравнению:

,

где F_i – последовательность чисел Фибоначчи.

Если принять начальный интервал неопределенности , то на основании формулы , можно показать, что

Т.о. положение первой точки измерения зависит от числа опытов N. В этом заключается отличие метода Фибоначчи – число шагов необходимо задать заранее.

Алгоритм:

Исходные данные: начальный интервал неопределенности [a;b], требуемое число шагов N.

1. Выбираем

2. Рассчитываем L₂ по формуле

3. – номер текущего шага

4. Определяем координату точки x₂ и симметричной ей x₁: ,

5. Вычисляем значения функции в точках x₁ и x₂: и

6. Если , то ,

если , то .

7.

8. Если i<N, то идем на шаг 5

9. Если i=N, то

Ввиду того, то в пакете MathCAD отсутствует встроенная функция расчета N-го члена последовательности Фибоначчи, то можно использовать формулу Бине:

Варианты заданий