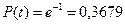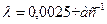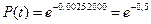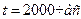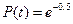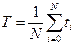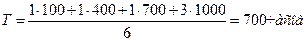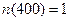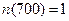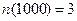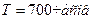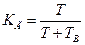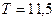КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зачет Д-410-3 Билет № 22
| № п/п | Содержание вопроса | ||||||||||||
В чем отличие понятий «Гамма-процентный ресурс» и «Ресурс»?
Гамма-процентный ресурс, tgрес — это суммарная наработка, в течение которой объект не достигнет предельного состояния с вероятностью g, выраженной в процентах.
Аналитически эта величина может быть найдена из выражения
F(tgрес) = 1 -  где F(tgрес)— функция распределения ресурса.
Обычно значение g устанавливают равным 95 для изделий с относительно большим ресурсом (полупроводниковые приборы, интегральные микросхемы и др.) и 90 — для изделий с ограниченными ресурсами (это в основном электровакуумные приборы).
Для определения гамма-процентного ресурса (статистической его оценки) ставят на испытание значительное число изделий и по мере их отказов строят кривую g (t) (рисунок 1). При g = 95% или g = 90% по графику определяют значение tgрес..
g, %
где F(tgрес)— функция распределения ресурса.
Обычно значение g устанавливают равным 95 для изделий с относительно большим ресурсом (полупроводниковые приборы, интегральные микросхемы и др.) и 90 — для изделий с ограниченными ресурсами (это в основном электровакуумные приборы).
Для определения гамма-процентного ресурса (статистической его оценки) ставят на испытание значительное число изделий и по мере их отказов строят кривую g (t) (рисунок 1). При g = 95% или g = 90% по графику определяют значение tgрес..
g, %
 t рес
0 t0,95рес t0,9рес
Рис. 1.
Понимать гамма-процентный ресурс надо следующим образом. Например, t0,95рес = 20 000 часов. Это значит, что данное изделие проработает не менее 20 000 часов с вероятностью g = 0, 95, или же, при наработке наработке в 20 000 часов сохранят работоспособность не менее 95% изделий.
Ресурс - это суммарная наработка объекта от начала его эксплуатации или ее возобновления после ремонта до перехода в предельное состояние. t рес
0 t0,95рес t0,9рес
Рис. 1.
Понимать гамма-процентный ресурс надо следующим образом. Например, t0,95рес = 20 000 часов. Это значит, что данное изделие проработает не менее 20 000 часов с вероятностью g = 0, 95, или же, при наработке наработке в 20 000 часов сохранят работоспособность не менее 95% изделий.
Ресурс - это суммарная наработка объекта от начала его эксплуатации или ее возобновления после ремонта до перехода в предельное состояние.
| |||||||||||||
| Какие свойства надежности характеризуют указанные показатели: гамма-процентная наработка до отказа, гамма-процентный срок службы, интенсивность восстановления, интенсивность отказов, вероятность отказов? гамма-процентная наработка до отказа, интенсивность отказов, вероятность отказов –показатели безотказности Безотказность невосстанавливаемых объектов оценивается количественно временем работы (наработкой) до отказа T. гамма-процентный срок службы, tgср. сл. -показатель долговечности Долговечность— свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта. интенсивность восстановления –показатель ремонтопригодности Ремонтопригодность - свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта. | |||||||||||||
При ориентировочном расчете надежности принимается допущение о том, что все элементы проектируемого устройства функционируют на этапе нормальной эксплуатации. Каким образом это допущение используется в методике расчета.
На участке нормальной эксплуатации значение интенсивности отказов практически постоянно, то есть не зависит от времени, следовательно, можно записать: l(t) =const.
Выражение для определения вероятности безотказной работы имеет вид:
 (*),
Таким образом, при l(t) =const распределение времени безотказной работы T подчиняется экспоненциальному закону. Выражение (* ) называют экспоненциальным законом надежности. При его использовании все задачи надежности решаются довольно просто. Отметим важное свойство этого закона: при экспоненциальном законе вероятность безотказной работы в интервале времени t+ (*),
Таким образом, при l(t) =const распределение времени безотказной работы T подчиняется экспоненциальному закону. Выражение (* ) называют экспоненциальным законом надежности. При его использовании все задачи надежности решаются довольно просто. Отметим важное свойство этого закона: при экспоненциальном законе вероятность безотказной работы в интервале времени t+ 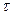 не зависит от предшествующей наработки, а определяется только длиной интервала не зависит от предшествующей наработки, а определяется только длиной интервала 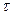 : :
 Средняя наработка до отказа при экспоненциальном законе надежности, как было определено выше, является интегральной величиной
Средняя наработка до отказа при экспоненциальном законе надежности, как было определено выше, является интегральной величиной
 Из этого выражения следует, что Т численно равна площади, ограниченной кривой Р(t) и осями координат. Но одна и та же площадь может быть ограничена кривыми различного вида.
Отсюда следует, что Т не полностью характеризует закон распределения отказов, а является лишь параметром. Для частного случая, когда изучается надежность изделия в период нормальной эксплуатации и можно принять
Из этого выражения следует, что Т численно равна площади, ограниченной кривой Р(t) и осями координат. Но одна и та же площадь может быть ограничена кривыми различного вида.
Отсюда следует, что Т не полностью характеризует закон распределения отказов, а является лишь параметром. Для частного случая, когда изучается надежность изделия в период нормальной эксплуатации и можно принять  ; ; 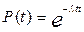 , то справедливо выражение , то справедливо выражение
 Тогда вероятность безотказной работы будет равна:
Тогда вероятность безотказной работы будет равна:
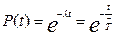 Таким образом, определены основные параметры безотказности невосстанавливаемых объектов.
Таким образом, определены основные параметры безотказности невосстанавливаемых объектов.
| |||||||||||||
Поясните физический смысл экспоненциального закона надежности.
При l(t) =const распределение времени безотказной работы T подчиняется экспоненциальному закону. Выражение 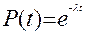 называют экспоненциальным законом надежности. При его использовании все задачи надежности решаются довольно просто. Отметим важное свойство этого закона: при экспоненциальном законе вероятность безотказной работы в интервале времени t+ называют экспоненциальным законом надежности. При его использовании все задачи надежности решаются довольно просто. Отметим важное свойство этого закона: при экспоненциальном законе вероятность безотказной работы в интервале времени t+ 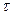 не зависит от предшествующей наработки, а определяется только длиной интервала не зависит от предшествующей наработки, а определяется только длиной интервала 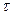 : :
 Средняя наработка до отказа при экспоненциальном законе надежности, как было определено выше, является интегральной величиной
Средняя наработка до отказа при экспоненциальном законе надежности, как было определено выше, является интегральной величиной  Из этого выражения следует, что Т численно равна площади, ограниченной кривой Р(t) и осями координат. Но одна и та же площадь может быть ограничена кривыми различного вида.
Отсюда следует, что Т не полностью характеризует закон распределения отказов, а является лишь параметром. Для частного случая, когда изучается надежность изделия в период нормальной эксплуатации и можно принять
Из этого выражения следует, что Т численно равна площади, ограниченной кривой Р(t) и осями координат. Но одна и та же площадь может быть ограничена кривыми различного вида.
Отсюда следует, что Т не полностью характеризует закон распределения отказов, а является лишь параметром. Для частного случая, когда изучается надежность изделия в период нормальной эксплуатации и можно принять  ; ; 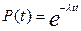 , то справедливо выражение , то справедливо выражение  Тогда вероятность безотказной работы будет равна:
Тогда вероятность безотказной работы будет равна: 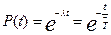 Таким образом, определены основные параметры безотказности невосстанавливаемых объектов.
Таким образом, определены основные параметры безотказности невосстанавливаемых объектов.
| |||||||||||||
Нарисовать пример структурной схемы надежности объекта с раздельным резервированием элементов.

| |||||||||||||
Определить максимально возможное число элементов проектируемого объекта, если интенсивность отказов элементов не больше, чем 10-7 1/час, а средняя наработка на отказ объекта не должна быть меньше 1000 часов.
Ответ:
Ответ:
| |||||||||||||
На участке нормальной эксплуатации интенсивность отказов невосстанавливаемого объекта равна 0,0025 1/ч. Какова вероятность его безотказной работы в течение 2000 часов?
Ответ: | |||||||||||||
На испытания длительностью 1000 часов поставлено 6 невосстанавливаемых объектов. Первый объект отказал через 100 ч., второй – через 400 ч., третий – через 700 ч., а остальные не отказывали. Определить статистическое значение средней наработки до отказа.
Ответ: | |||||||||||||
| Система состоит из 2 равных по надежности восстанавливаемых элементов, причем отказ любого из них приводит к отказу системы. Определить значения наработки на отказ элементов, если известно, что для всей системы Кг = 0,92 и ТВ = 1 час
| |||||||||||||
| Пусть имеется многоканальная аппаратура передачи данных, имеющая 10 каналов связи? Пусть, также для обеспечения связи требуется только 8 каналов. Вычислите Кг аппаратуры с учетом резервирования. Назовите вид резервирования. | |||||||||||||
| Опишите модель объекта диагностирования в виде таблицы функции неисправностей. | |||||||||||||
| Приведите пример ситуации, когда условный алгоритм диагностирования оказывается менее эффективным, чем безусловный. | |||||||||||||
| Почему при построении модели объекта диагностирования в виде графа информационно-энергетических связей сначала строится как минимум два самостоятельных ГИЭС? | |||||||||||||

| Для вершин изображенного на рисунке ГИЭС определить индексы предшествования. На основе ГИЭС построить ДЛВ по структурному критерию | ||||||||||||
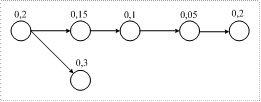
| Для вершин изображенного на рисунке ГИЭС определить значения функции предпочтительного выбора. На основе ГИЭС построить ДЛВ по вероятностному критерию |
Дата добавления: 2015-02-10; просмотров: 308; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 час-1
час-1
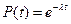
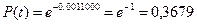
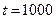 час
час