Методы генерации псевдослучайных последовательностей чисел

При шифровании методом гаммирования в качестве ключа используется случайная строка битов, которая объединяется с открытым текстом, также представленным в двоичном виде (например, А= 00000, В =00001, С =00010 и т.д ), с помощью побитового сложения по модулю 2, и в результате получается шифрованный текст. Генерирование непредсказуемых двоичных последовательностей большой длины является одной из важных проблем классической криптографии. Для решения этой проблемы широко используются генераторы двоичных псевдослучайных последовательностей.

Генерируемые псевдослучайные ряды чисел часто называют гаммой шифра или просто гаммой (по названию буквы у греческого алфавита, часто используемой в математических формулах для обозначения случайных величин).

Обычно для генерации последовательности псевдослучайных чисел применяют компьютерные программы, которые, хотя и называются генераторами случайных чисел, на самом деле выдают детерминированные числовые последовательности, которые по своим свойствам очень похожи на случайные.

К криптографически стойкому генератору псевдослу тайной последовательности чисел (гаммы шифра) предъявляются три основных требования:

· период гаммы должен быть достаточно большим для шифрования сообщений различной длины;

· гамма должна быть практически непредсказуемой, что означает невозможность предсказать следующий бит гаммы, даже если известны тип генератора и предшествующий кусок гаммы;

· генерирование гаммы не должно вызывать больших технических сложностей.

Один из первых способов генерации псевдослучайных чисел а ЭВМ предложил в 1946г. Джон фон Нейман. Суть этого способа остоит в том, что каждое последующее случайное число образуется возведением в квадрат предыдущего числа с отбрасыванием цифр младших и старших разрядов Однако этот способ оказался ненадежным и от него вскоре отказались

Из известных процедур генерации последовательности псевдослучайных целых чисел наиболее часто применяется так называемый линейный конгруэнтный генератор Этот генератор вырабатывает последовательность псевдослучайных чисел используя соотношение

(3.13)

где , - i-e (текущее) число последовательности; - предыдущее число последовательност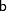и; , и 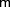- константы; 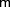- модуль, - множитель (коэффициент); 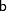- приращение, 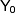- порождающее число (исходное значение).

Конгруэнтные генераторы, работающие по алгоритму, предложенному Национальным бюро стандартов США, используются, в частности, в системах программирования Эти генераторы имеют длину периода 224 и обладают хорошими статистическими свойствами Однако такая длина периода мала для криптографических применений Кроме того, доказано, что последовательности, генерируемые конгруэнтными генераторами, не япляются криптографически стойкими.

Существует способ генерации последовательностей псевдослучайных чисел на основе линейных рекуррентных соотношений.

Рассмотрим рекуррентные соотношения и их разностные уравнения:

где , и каждое 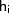, принадлежит полю Решением этих уравнений является последовательность элементов поля . Это соотношение определяет правило вычисления по известным значениям величин . Затем по известным значениям находят и т.д. В результате по начальным значениям можно построить бесконечную последовательность, причем каждый ее последующий член определяется из предыдущих. Последовательности такого вида легко реализуются на компьютере, при этом реализация получается, если все 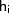и , принимают значения 0 и I из поля .

Для криптографии последовательности максимальной длины MLSRS можно сделать более криптостойкими, используя нелинейную логику. В частности, предложен вариант, в котором в качестве ключевого потока используется нелинейно "фильтрованное" содержимое сдвигового регистра, а для получении последовательности максимальной длины - линейная обратная связь, как показано на рис. 3.17.

Рис. 3.17 Линейный сдвиговый регистр с нелинейными логическими цепями на выходе.

Функция должна выбираться так, чтобы обеспечить хороший баланс между нулями и единицами, а фильтрованная последовательность имела распределение, близкое к равномерному Необходимо также, чтобы фильтрованная последовательность имела большой период. Если является простым числом (как в примере при 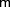имеем ), то фильтрованная последовательность может иметь период (при выборе структуры сдвигового регистра в соответствии с неприводимым примитивным многочленом степени ).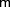

К таким значениям 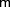относятся, в частности, следующие 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, а полученные таким обрашм простые числа называются простыми числами Мерсенна.

Несмотря на то, что фильтрованную выходную последовательность обычно нельзя получить с помощью m-разрядного сдвигового регистра с линейной обратной связью, ее всегда можно получить с помощью сдвигового регистра большей длины с линейной обратной связью . Регистр длиной всегда позволит это сделать, а иногда притуден н более короткий регистр.

Еше более привлекательно использование в цепи обратной связи нелинейной логики, однако теория таких схем недостаточно хорошо освещена.