
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
МОДУЛЯЦИЯ
Преобразование измерительной информации с целью передачи ее по каналу связи называется модуляцией. Носителями информации в различных каналах связи могут быть электромагнитные колебания оптического, радио и более низкочастотных диапазонов, акустические колебания и т.п. Они характеризуются такими параметрами, как амплитуда колебаний, частота, начальная фаза или, например, параметрами поляризации электромагнитного излучения. Если эти параметры остаются неизменными, то, несмотря, например, на излучение и прием электромагнитных колебаний, никакой передачи информации не происходит. Информация передается тогда, когда изменение (модуляция) одного из параметров отражает ее содержание. Естественно при этом, что на приемном пункте изменение параметра должно быть обратно преобразовано в сигнал, представляющий собой информацию (в частности - измерительную). Такое обратное преобразование называется демодуляцией.
В зависимости от того, за счет изменения какого параметра осуществляется передача информации по каналу связи, различают амплитудную, частотную, фазовую, поляризационную и другие виды модуляции. Рассмотрим наиболее распространенные из них.
Амплитудная модуляция. При аналоговой форме представления измерительной информации чаще всего применяется амплитудная модуляция. Если немодулированное несущее колебание имеет вид гармонической функции
У0 (t) = A0 cos (ω0 t+φ0),
где A0, ω0 и φ0 — соответственно амплитуда, круговая частота и начальная фаза этого колебания, то амплитудно-модулированное колебание описывается выражением
У (t) = [A0 +Х (t)]cos (ω0 t+φ0),
где X (t) — сигнал на выходе средства измерений, заключающий в себе измерительную информацию. Если, предположим,
Х (t) = В cos Ωt, где частота модуляции Ω» ω0,то
Y (t) = А0 (1 + m cos Ω t) cos (ω0t+ φ0),
a параметр m =  ≤1 называется глубиной модуляции.
≤1 называется глубиной модуляции.
Этот пример иллюстрируется рис. 167.
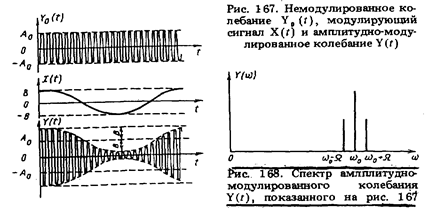
Спектр амплитудно-модулированного колебания не содержит составляющей на частоте модуляции. В рассматриваемом примере представление о нем можно получить, преобразовав последнее выражение следующим образом:

Спектр симметричен относительно составляющей на несущей частоте ω0 и состоит еще из двух составляющих на боковых частотах ω0 – Ω и ω0 +Ω с амплитудами m  (см. рис. 168).Ширина спектра равна 2Ω, что вдвое превышает ширину спектра модулирующего сигнала Х (t).
(см. рис. 168).Ширина спектра равна 2Ω, что вдвое превышает ширину спектра модулирующего сигнала Х (t).
При сложных модулирующих сигналах спектр модулированного колебания получается более богатым. Так, при
Х (t) =  cos (nWt + jn)
cos (nWt + jn)
спектральный состав амплитудно-модулированного колебания определяется выражением:

Характер такого спектра показан на рис. 169.
Спектральная составляющая на несущей частоте не несет в себе информацию о модулирующем сигнале. Следовательно, на ее передачу по каналу связи непроизводительно расходуется мощность передающего устройства. Для устранения этого недостатка применяется балансная амплитудная модуляция, при которой оставляющая на несущей частоте в спектре амплитудно-модулированного колебания отсутствует. Достигается это прямым умножением Y0 (t) на X(t). Так, в частности в последнем случае

и спектр амплитудно-модулированного колебания состоит только из составляющих на боковых частотах.
Симметрия спектра амплитудно-модулированного колебания позволяет и более экономно расходовать мощность передающего устройства. Можно передавать составляющие в спектре, лежащее только по одну из сторон от несущей частоты. В этом случае вдвое сокращается ширина спектра амплитудно-модулированного сигнала, но усложняется аппаратура.
Аппаратурная реализация амплитудной модуляции предполагает выполнение операции умножения. Следовательно, модулятор должен включать в себя аналоговое перемножающее устройство. В линейных цепях с переменными параметрами для этого используются электронные лампы, транзисторы или операционные усилители с управляемым коэффициентом усиления. Другим способом является использование нелинейных элементов, на которые подаются, например, напряжения
u1=A0cosw0t
u2=BcosWt
Электрический ток в цепи, включающей нелинейный элемент является функцией этих напряжений, разложив которую в ряд Тейлора по ее аргументам, получим:
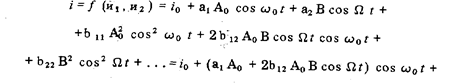
где i0, a и b - постоянные. Последнее слагаемое, представляющее собой амплитудно-модулированное колебание может быть, выделено резонансным элементом с шириной полосы пропускания, перекрывающей спектр этого колебания.
Частотная модуляция. При частотной модуляции сигнал, содержащий измерительную информацию меняет частоту модулируемого колебания

Если, например,

где Ω - по-прежнему, частота модуляции, а ∆ω называется девиацией частоты, то

где m = 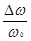 - глубина модуляции частоты. Этот пример иллюстрирует рис. 170.
- глубина модуляции частоты. Этот пример иллюстрирует рис. 170.
Круговая частота по определению представляет собой производную по времени от мгновенной фазы колебания В рассматриваемом примере она равна ω0(1 + m cosΩt). Следовательно, мгновенная фаза


где mчм =  — индекс частотной модуляции. С учетом начальной фазы
— индекс частотной модуляции. С учетом начальной фазы
Y (t) = A0 cos (ω0 t + mчмsin Ωt + φ0 ) .
Представление о спектре рассматриваемого частотно-модулированного колебания можно получить, если представить последнее выражение в виде
Y(t) = A0 cos (ω0 t+φ0) cos (mчм sin Ωt) — A0 sin (ω0 t+φ0) sin (m чмsinΩt).
В общем случае для его анализа нужно воспользоваться следующими разложениями по функциям Бесселя:
cos (x sin у) =J0 (x ) + 2 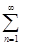 J2n (x) cos 2 nу;
J2n (x) cos 2 nу;
sin (x sin y) = 2  J2n+1 (x) sin (2 n + 1) у.
J2n+1 (x) sin (2 n + 1) у.
Для простоты ограничимся случаем малого индекса частотной модуляции m чм « 1. Тогда можно принять

и записать выражение для частотно-модулированного колебания в виде

Таким образом, при mчм«1 спектр частотно-модулированного колебания не отличается от спектра амплитудно-модулированного колебания, показанного на рис. 168 (при одинаковом модулирующем сигнале). Если условие mчм«1 не выполняется, что характерно для глубокой частотной модуляции, то спектр частотно-модулированного сигнала содержит не две, а гораздо больше боковых частот. В общем случае, следовательно,спектр частотно-модулированного сигнала шире, чем амплитудно-модулированного.
Технически частотно-модулированные колебания получают обычно, воздействуя модулирующим сигналом на один из параметров, определяющих частоту генератора.
Фазовая модуляция. При фазовой модуляции сигналом, содержащим измерительную информацию, изменяется начальная фаза модулируемого колебания

Если, по-прежнему, рассматривать гармонический модулирующий сигнал
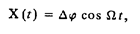
Дата добавления: 2015-02-10; просмотров: 252; Мы поможем в написании вашей работы!; Нарушение авторских прав |