
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аралық бақылау бойынша сұрақтар мен тапсырмалар тізімі
Стр 1 из 2Следующая ⇒
Студенттердің оқу жетістіктерін бағалау және бақылау бойынша материалдар
аралық бақылау бойынша сұрақтар мен тапсырмалар тізімі
| № п.п | Сұрақтары |
| 1) | 2-ші ретті анықтауышты есептеңіз: 
|
| 2) | 3-ші ретті анықтауышты есептеңіз: 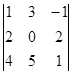
|
| 3) | Қасиеттерін пайдаланып, 3-ші ретті анықтауышты есептеңіз: 
|
| 4) | Анықтауышты жолдарының бірінің элементтері бойынша жіктеп, мәнін табыңыз: 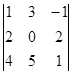
|
| 5) |  анықтауыштың М21 минорын табыңыз: анықтауыштың М21 минорын табыңыз:
|
| 6) | Теңдеуден белгісіз Х табыңыз  =0 =0 
|
| 7) | Ықшамдап, мәнін табыңыз: 
|
| 8) | Анықтауыштарды пайдаланып, теңдеулер жүйесін шешіңіз: 
|
| 9) | (2х3) өлшемді матрицаны көрсетіңіз: 
|
| 10) | Берілген екі матрицаның қосындысын, А+В=С матрицасын табыңыз: 
|
| 11) | А*В көбейтіндісін есептеңіз,егер 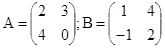
|
| 12) | Бірлік матрицаны көрсетіңіз: 
|
| 13) | Мыналардың қайсысы түрленген матрица: 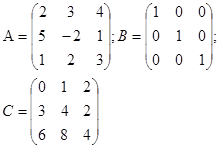
|
| 14) | А матрицасына кері матрицаны табыңыз: 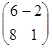
|
| 15) |  Есептеңіз: Есептеңіз: 
|
| 16) |  Есептеңіз: Есептеңіз:  М32 минорын М32 минорын
|
| 17) | Есептеңіз:  М31 минорын М31 минорын
|
| 18) | А матрицасының нөлге тең емес минорының ең үлкен реті қалай аталады? |
| 19) | Матрицасының рангын табыңыз 
|
| 20) |  Матрицасының рангын табыңыз Матрицасының рангын табыңыз
|
| 21) | A= 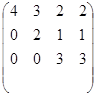 Матрицасының рангын табыңыз Матрицасының рангын табыңыз
|
| 22) | 2А+5В матрицасын табу керек,егер 
|
| 23) | А2=А*А матрицасын табу керек, егер 
|
| 24) | А=  матрицасы берілген. А матрицасына қандай В матрицасын қосқанда бірлік матрица шығады? матрицасы берілген. А матрицасына қандай В матрицасын қосқанда бірлік матрица шығады?
|
| 25) | А=  матрицасы берілген. А матрицасына қандай В матрицасын қосқанда бірлік матрица шығады? матрицасы берілген. А матрицасына қандай В матрицасын қосқанда бірлік матрица шығады?
|
| 26) | А= 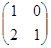 және В= және В=  матрицаларының көбейтіндісін табыңыз: матрицаларының көбейтіндісін табыңыз:
|
| 27) |  және және  түзулерінің қиылысу нүктесін табыңыз: түзулерінің қиылысу нүктесін табыңыз:
|
| 28) |  векторының координаталарын табыңыз, егер А(2; 3; 1) және В(-2; 0; 1) векторының координаталарын табыңыз, егер А(2; 3; 1) және В(-2; 0; 1)
|
| 29) |  векторының ұзындығын табыңыз, егер А(2; 3; 1) және В(-2; 0; 1): векторының ұзындығын табыңыз, егер А(2; 3; 1) және В(-2; 0; 1):
|
| 30) |  = {3; 4; 0} векторының бағыттауыш косинустарын табыңыз: = {3; 4; 0} векторының бағыттауыш косинустарын табыңыз:
|
| 31) | с = ā + b векторының координаталарын табыңыз, егер  ā ={2; 3} және в{-4; 5}. ā ={2; 3} және в{-4; 5}.
|
| 32) | 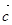 = 2 ā + b векторының координаталарын табыңыз, егер ā = {1; 0} және = 2 ā + b векторының координаталарын табыңыз, егер ā = {1; 0} және  ={3; 4} берілген болса ={3; 4} берілген болса
|
| 33) | |с| = 2 ā + b, |с| табыңыз, егер ā = {1; 0}, b = { 3; 4} |
| 34) | Мына векторлардың қайсылары өзара параллель ā = {1; 4}, b = {0; 4}, 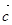 = {1; 0}, = {1; 0},  = {2; 8} = {2; 8}
|
| 35) | Мына векторлардың қайсылары өзара перпендикуляр:ā = {1; 4}, b = {0; 4}, с = {-4; 1}, d = {4; 6} |
| 36) | Мына векторлардың арасындағы бұрышты табыңыз  ={1;1;0} ={1;1;0}  ={1;2;2} ={1;2;2}
|
| 37) | a·b векторының скаляр көбейтіндісін табыңыз егер,  ={-1;1;0}, ={-1;1;0},  ={1;-2;2} ={1;-2;2}
|
| 38) |  ={1;-3;5} векторына қарама-қарсы вектордың координаталарын табыңыз: ={1;-3;5} векторына қарама-қарсы вектордың координаталарын табыңыз:
|
| 39) | Төбелері А(-4;2), В(0;-1),С(3;3) нүктелерінде жатқан үшбұрыштың периметрін табыңыз: |
| 40) | А(-2; 1) және В(3; 6) нүктелері берілген. АВ қақ бөлетін М нүктесінің координаталарын табыңыз: |
| 41) | с =  , векторының координаталарын табыңыз,егер ā = {3; 0; 0},b = {0; 0; 2} , векторының координаталарын табыңыз,егер ā = {3; 0; 0},b = {0; 0; 2}
|
| 42) | ā = {1; 1; 0}, b = {1;-1; 2} векторларын қабырғалары етіп тұрғызылған үшбұрыштын ауданын табыңыз |
| 43) | ā = {1; 0; 0}, b= {0; 1; 1}, с = {0; 0; 1} векторларын қырлары етіп тұрғызылған параллелепипедтің көлемін табыңыз. |
| 44) | ā={3; 4; 0}, b={0;-3; 1}, с = {0; 2; 5} векторларының аралас көбейтіндісін табыңыз: |
| 45) | Мына векторлардың қай үштігі өзара компланар: ā = {-1; 3; 2}, b = {2; -3; -4}, с = {-3;9; 6} d= {4; 0; 0} |
| 46) | y=kx + b түзуінің бұрыштық коэффициенті тең tg φ, егер φ – |
| 47) | Нөлдік вектор деп мына вектор аталады: |
| 48) | Эллипстің жарты осьтерін табыңыз:  : :
|
| 49) |  векторының ұзындығын табыңыз,егер С (0;5;1), D(-3;5;5) векторының ұзындығын табыңыз,егер С (0;5;1), D(-3;5;5)
|
| 50) | у = 5х +7 және у = 5х – 1 түзулерінің арасындағы бұрышты табыңыз: |
| 51) | 1) 3х – 2у + 7 = 0, 2) 6х – 4у – 9 = 0, 3) 6х + 4у –5 = 0, 4) 2х +3у – 6 = 0 түзулерінің қайсылары өзара параллель екенін көрсетіңіз |
| 52) | 1) 3х – 2у + 7 = 0, 2) 6х – 7у – 9 = 0, 3) 6х + 4у –5 = 0, 4) 2х +3у – 6 = 0 түзулердің қайсылары өзара перпендикуляр |
| 53) | А(-1; 3) және В(4; -2) нүктелері арқылы өтетін түзудің теңдеуін жазыңыз |
| 54) | А(-1; -1), В(3; 2), О(0; 0), С(1; 1) нүктелерінің қайсылары (х + 4)2 + (у – 3)2 = 25 шеңбердің бойында жатады |
| 55) | Гиперболаның жарты осьтерін табыңыз: 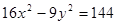
|
| 56) | Төбесі бас нүктеде жатқан, Ох осіне симметриялы және М(1;-4) нүктесінен өтетін параболаның теңдеуін түзіңіз: |
| 57) | Бұрыштық коэффициенті k = 7 және M (1; -5) нүктесі арқылы өтетін түзудің теңдеуін құрастыр. |
| 58) | х2 + у2 + 4у = 0 шеңберінің радиусын жазыңыз: |
| 59) | х2 + 4у2 = 16 элипстің үлкен және кіші осьтерін табыңыз: |
| 60) | 4х2 – у2 =16 гиперболасының үлкен және кіші жарты осьтерін табыңыз: |
| 61) | Мына нүктелерінің қай екеуі у2 = 6х параболасының бойында жатады: (0; 0), (3; 3), (2; 4), (6; 6) |
| 62) | М(5; -3; 4) нүктесінің вектор ұзындығының радиусын табыңыз: |
| 63) | ā = 2i + 3j + 6k векторының ұзындығын (модулін) табыңыз |
| 64) | Мына түзулердің 2х + 5у – 1 = 0 және 5х –2у +3 = 0 арасындағы бұрышты табыңыз: |
| 65) |  (4,-1) және (4,-1) және  (2,5) векторларының скаляр көбейтіндісін тап: (2,5) векторларының скаляр көбейтіндісін тап:
|
| 66) |  (0,1) және (0,1) және  (1,0) векторларының арасындағы бұрышты есептеңіз: (1,0) векторларының арасындағы бұрышты есептеңіз:
|
| 67) | Кесіндінің екі ұшы берілген: А(0;-5), В(4;7). Сол кесіндіні  = 3 қатынасында бөлетін нүктені табыңыздар = 3 қатынасында бөлетін нүктені табыңыздар
|
| 68) | Түзудің параметрлік теңдеуін құрастырыңыз: 
|
| 69) | Шеңбердің центрі С(-1;3) және радиусы 1 –ге тең. Осы шеңбердің теңдеуін табыңыздар: |
| 70) | Есептеңіз: 
|
| 71) | f(x) = 3x3 – 9x2+5 функциясының ойыстығының интервалын аңықтаңыз: |
| 72) | y = 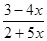 қисығының вертикаль асимптотасын табыңыз: қисығының вертикаль асимптотасын табыңыз:
|
| 73) | y=  қисығының горизонталь асимптотасын табыңыз: қисығының горизонталь асимптотасын табыңыз:
|
| 74) | y =  қисығының көлбеу асимптотасын табыңыз: қисығының көлбеу асимптотасын табыңыз:
|
| 75) | Берілген y= 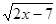 функциясының анықталу облысын табыңыз: функциясының анықталу облысын табыңыз:
|
| 76) | Берілген y =  функциясының анықталу облысын табыңыз: функциясының анықталу облысын табыңыз:
|
| 77) | у=х 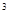 -1 функциясы берілді. f(1) табыңыз. -1 функциясы берілді. f(1) табыңыз.
|
| 78) | у=х 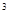 +1 функциясы берілді. f(1) табыңыз. +1 функциясы берілді. f(1) табыңыз.
|
| 79) | Мынадай функция монотонды деп аталады: |
| 80) | Функцияның кемуінің жеткілікті шартына сәйкес ,  функциясы кемімелі функциясы кемімелі 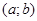 , егер , егер
|
| 81) | Мына функцияның туындысын тап: 
|
| 82) | Жұп функцияның мынадай қасиеті бар. |
| 83) | у = tg x функциясының периодын көрсетіңіз: |
| 84) | Айқын емес түрде берілген функцияны көрсетіңіз:
1)   2)
2) 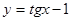 3)
3)  4)
4)  5)
5) 
|
| 85) | Мына функциялардың қайсылары күрделі функциялар
1)  2) y = sin (2x-1)
3) y = x +5
4) y = cos x
5) y = tg x
2) y = sin (2x-1)
3) y = x +5
4) y = cos x
5) y = tg x
|
| 86) | Сандар тізбегінің қысқаша анықтамасын тұжырымдаңыз. |
| 87) | Сандар тізбегінің жинақталатын тізбек деп аталады,егер? |
| 88) | 
|
| 89) | Функцияның туындысын тап: 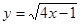 : :
|
| 90) | Экстремумның бірінші жеткілікті шартына сәйкес, 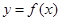 функциясының х0 нүктесінде максимум, егер: функциясының х0 нүктесінде максимум, егер:
|
| 91) | 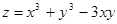 функциясының стационар нүктесін табыңыз: функциясының стационар нүктесін табыңыз:
|
| 92) |  функциясының функциясының  табыңыз: табыңыз:
|
| 93) | Екі функцияның көбейтіндісі u ν туындысы мына ережемен табылады |
| 94) | Екі функцияның қатынасы  -ның туындысы мына ережемен табылады: -ның туындысы мына ережемен табылады:
|
| 95) | Тұрақты шаманың санның туындысы неге тең? |
| 96) | у = sin (lnx) функциясының х0=1 нүктесіндегі туындысын табыңыз. |
| 97) | Шек есепте: 
|
| 98) | Шек есепте: 
|
| 99) | Шек есепте: 
|
| 100) | Функцияның үзіліс нүктелерін табыңыз 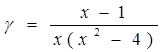
|
| 101) | Функцияның анықталу облысын табыңыз 
|
| 102) | Функцияның анықталу облысын табыңыз 
|
| 103) | Функцияның анықталу облысын табыңыз 
|
| 104) | Функцияның анықталу облысын табыңыз 
|
| 105) | Функцияның анықталу облысын табыңыз 
|
| 106) | Функцияның анықталу облысын табыңыз 
|
| 107) | 
|
| 108) | 
|
| 109) | 
|
| 110) | 
|
| 111) | 
|
| 112) | 
|
| 113) | 
|
| 114) | 
|
| 115) | 
|
| 116) | Шек есепте: 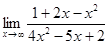
|
| 117) | Шек есепте: 
|
| 118) | Есепте: 
|
| 119) | Шек есепте: 
|
| 120) | Шек есепте: 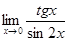
|
| 121) | Шек есепте: 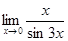
|
| 122) | Шек есепте: 
|
| 123) | Шек есепте: 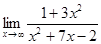
|
| 124) | Шек есепте: 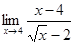
|
| 125) | Шек есепте: 
|
| 126) | Шек есепте: 
|
| 127) | Шек есепте: 
|
| 128) | Шек есепте: 
|
| 129) | Шек есепте: 
|
| 130) | Шек есепте: 
|
| 131) | Шек есепте: 
|
| 132) | Шек есепте: 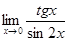
|
| 133) | Шек есепте: 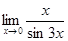
|
| 134) | Шек есепте: 
|
| 135) | Ақырсыз үлкен шаманы көрсет |
| 136) |  функциясының анықталу облысын тап функциясының анықталу облысын тап
|
| 137) |  функциясының максимумын тап функциясының максимумын тап
|
| 138) | 
|
| 139) |  (с-тұрақты)
(с-тұрақты)
|
| 140) | 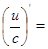 (с-тұрақты) (с-тұрақты)
|
| 141) | 
|
| 142) | y=tgx функциясының туындысын табыңыз: |
| 143) | y=ctgx функциясының туындысын табыңыз: |
| 144) | y=ax функциясының туындысын табыңыз: |
| 145) | y=arctgx функциясының туындысын табыңыз: |
| 146) | y=arccosx функциясының туындысын табыңыз: |
| 147) | y=ln(ax+b) функциясының туындысын табыңыз: |
| 148) | Екі функцияның қосындысының туындысының формуласын жазыңыз: (u+v) |
| 149) | Функцияның туындысын табыңыз: y=k  f(x) f(x)
|
| 150) | y=sin x функциясының 2-ші ретті туындысын табыңыз: |
| 151) | y=f(x) функциясының дифференциалын жазыңыз: |
| 152) |  функциясының туындысын табыңыз функциясының туындысын табыңыз 
|
| 153) | Функцияның туындысын табыңыз: y=k  f(x) f(x)
|
| 154) | y=sin x функциясының 2-ші ретті туындысын табыңыз: |
| 155) | y=f(x) функциясының дифференциалын жазыңыз: |
| 156) |  функциясының туындысын табыңыз функциясының туындысын табыңыз 
|
| 157) | Функцияның туындысын тап 
|
| 158) | Функцияның туындысын тап 
|
| 159) | 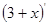
|
| 160) | 
|
| 161) | 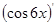
|
| 162) | 
|
| 163) | 
|
| 164) | 
|
| 165) | 
|
| 166) | 
|
| 167) | Функцияның туындысын тап 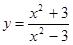 : :
|
| 168) | Функцияның туындысын тап 
|
Дата добавления: 2015-02-10; просмотров: 285; Мы поможем в написании вашей работы!; Нарушение авторских прав |