
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аралық бақылау бойынша сұрақтар мен тапсырмалар тізімі.
⇐ ПредыдущаяСтр 2 из 2
| | Ζ=x2+y2 Функциясының дербес туындыларын есептеңіз: |
| 2. | Функцияның толық дифференциал ын табыңыз: z=xy |
| 3. | z =4/(x+y) функциясының анықталу облысын табыңыз: |
| 4. | z=4/(x²+y²) функциясының анықталу облысын табыңыз: |
| 5. | Екі айнымалысы бар функцияның экстремумының болуының қажетті шартын жазыңыз : |
| 6. |  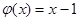 . Күрделі функция құрастырыңыз . Күрделі функция құрастырыңыз 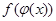 : :
|
| | 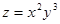 функциясының М(-1,1) нүктесіндегі l(4,3) векторының бағытындағы туындысын табыңыз: функциясының М(-1,1) нүктесіндегі l(4,3) векторының бағытындағы туындысын табыңыз:
|
| 8. | 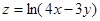 функциясының М(2,1) нүктесіндегі градиент бағытындағы туындысын табыңыз: функциясының М(2,1) нүктесіндегі градиент бағытындағы туындысын табыңыз:
|
| 9. | z=хcos y функциясының М (1, 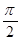 )нүктесіндегі grad z –ті табыңыз )нүктесіндегі grad z –ті табыңыз
|
| 10. | 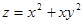 функциясының М(-1,-2) нүктесіндегі дербес туындылары функциясының М(-1,-2) нүктесіндегі дербес туындылары 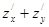 -ті -ті
|
| 11. | 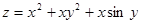 функциясының М(1,0) нүктесіндегі аралас туындысы функциясының М(1,0) нүктесіндегі аралас туындысы 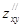 табыңыз табыңыз
|
| 12. | u=xyz функциясының М(2,1,1) нүктесіндегі градиент бағытындағы туындысын табыңыз |
| 13. | Берілді : у=z 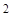 , z =х+1. у –ті х функциясы арқылы өрнекте: , z =х+1. у –ті х функциясы арқылы өрнекте:
|
| 14. | Z=  Максимум шартын жаз Максимум шартын жаз
|
| | Z=  минимум шартын жаз минимум шартын жаз
|
| |  , ,   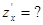
|
| |  , ,   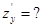
|
| |  , ,   
|
| | 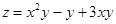 , ,   
|
| |  , ,   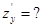
|
| | 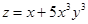 , ,   
|
| | 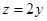 , ,   
|
| | 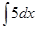
|
| | 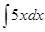
|
| | 
|
| | 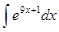
|
| | 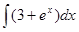
|
| | 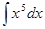
|
| | 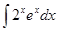
|
| | 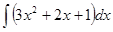
|
| | 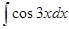
|
| | 
|
| | 
|
| | 
|
| | 
|
| | 
|
| | 
|
| | Интеграл есепте 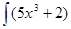 dx: dx:
|
| | 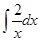
|
| | Анықталмаған интегралдың мынадай қасиеті бар: |
| | Мына қосынды интегралдық қосынды деп аталады |
| 42. | Интегралды есепте 
|
| | Анықталған интегралдың геометриялық мағынасы 
|
| | Интегралды есепте 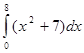 : :
|
| | 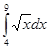  
|
| | 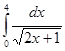
|
| | 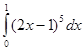
|
| | 
|
| | 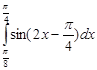 = =
|
| | 
|
| | 
|
| | 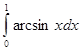
|
| | 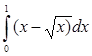
|
| | :

|
| | Интегралды есепте 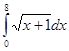 : :
|
| | 
|
| | О ху координаталар жүйесінде берілген, у=х2, у=0, х=3, сызықтармен шектелген жазық. Фигураның ауданы мынаған тең: |
| 58. | Оху координаталар жүйесінде берілген, y=sinx, y=0, x=  сызықтармен шектелген жазық фигураның ауданы мынаған тең: сызықтармен шектелген жазық фигураның ауданы мынаған тең:
|
| 59. | Синусоиданың бірінші толқынымен және Ох осімен шектелген жазық фигура Ох осінен айналғанда шығатын дененің көлемі тең: |
| 60. | y=2x, y=0, x=2 түзулерімен шектелген жазық фигура Ох осінен айналғанда шығатын дененің көлемі тең: : |
| 61. | 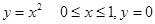 . S=? . S=?
|
| | 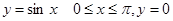 . S=? . S=?
|
| |  , ,  . S=? . S=?
|
| | Меншіксіз интеграл 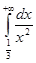 : :
|
| 65. | Меншіксіз интеграл 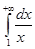 : :
|
| 66. | 1-ші ретті дифференцилдық теңдеудің жалпы түрін жазыңыз: |
| 67. |  теңдеуінің жалпы шешімін табыңыз: теңдеуінің жалпы шешімін табыңыз:
|
| 68. | Теңдеуді шешіңіз: y/=2x-y |
| 69. | Теңдеуді шешіңіз: y/=tgx tgy |
| 70. | Теңдеуді шешіңіз: 
|
| 71. | Теңдеуді шешіңіз: 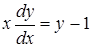
|
| 72. | Жалпы интегралын табыңыз: 
|
| 73. | Дифференциалдық теңдеудің реті деп мынаны атайды? |
| 74. | Берілген теңдеудің ішінен дифференциалдық теңдеуді атаңыз: |
| 75. | Теңдеуді шешіңіз: 
|
| 76. | Теңдеуді шешіңіз: y//-x2=0 |
| | Теңдеуінің жалпы шешімін табыңыз: y``-y`=0 |
| | Теңдеуінің жалпы шешімін табыңыз: y``-7y`+6y=0 |
| | Теңдеуінің жалпы шешімін табыңыз: y``-y`-2y=0 |
| | Теңдеуінің жалпы шешімін табыңыз: y``-2y`=0 |
| | Сызықтық дифференциалдық теңдеудің жалпы түрі: |
| 82. | Теңдеу шешіңіз 
|
| | Теңдеу шешіңіз 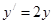
|
| | Теңдеу шешіңіз 
|
| | Теңдеу шешіңіз 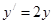 +1 +1
|
| | Теңдеу шешіңіз 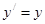
|
| | Теңдеу шешіңіз 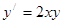
|
| | Теңдеу шешіңіз 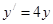
|
| | Теңдеу шешіңіз 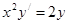
|
| | Теңдеу шешіңіз 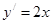
|
| | Қатар жинақтылығының қажетті шартты |
| | 1+1/2+1/3+1/4+…+1/n қатары деп аталады |
| 93. | Қатар жинақты, егер мынадай шарт орындалса |
| 94. |  функциясының Маклорен катарына жіктелуі: функциясының Маклорен катарына жіктелуі:
|
| 95. | Сандық қатар қай уақытта жинақы емес деп аталады: |
| 96. | Сандық қатардың 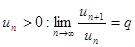 Даламбер белгісі бойынша жинақы болады, егер: Даламбер белгісі бойынша жинақы болады, егер:
|
| 97. | Қатардын алғашқы бес мүшесін есептеңіз 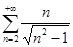 : :
|
| 98. | Даламбер белгісінің көмегімен қатарды жинақтылыққа зерттеңіз: 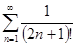
|
| | Даламбер белгісінің көмегімен қатарды жинақтылыққа зерттеңіз: 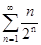
|
| | Даламбер белгісінің көмегімен қатарды жинақтылыққа зерттеңіз: 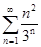
|
| | Даламбер белгісінің көмегімен қатарды жинақтылыққа зерттеңіз: 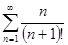
|
| | Коши белгісінің көмегімен қатарды жинақтылыққа зерттеңіз: 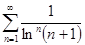
|
Дата добавления: 2015-02-10; просмотров: 290; Мы поможем в написании вашей работы!; Нарушение авторских прав |