Примеры решения задач. Пример 1.Кинематическое уравнение движения материальной точки по прямой имеет вид , где ,

Пример 1.Кинематическое уравнение движения материальной точки по прямой имеет вид , где , , . Для момента времени определить: 1) координату точки; 2) мгновенную скорость ; 3) мгновенное ускорение ; 4) среднюю скорость за промежуток времени с момента начала движения до .

Решение

1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения заданное значение времени :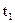

.

Подставив в это выражение значения постоянных А, В, С, и 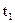, произведем вычисления: .

2. Уравнение, описывающее зависимость скорости от времени, найдем, продифференцировав координату 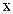по времени: . Тогда в заданный момент времени 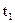мгновенная скорость .

Подставим сюда значения В, С, 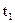и произведем вычисления:

.

Знак минус в полученном значении скорости указывает на то, что в данный момент времени скорость материальной точки направлена в сторону, противоположную положительному направлению оси X.

3. Функциональную зависимость ускорения от времени найдем, используя определение ускорения, как второй производной от координаты 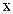по времени:

.

Подставим значения С, и произведем вычисления

.

4. По определению, среднее значение скорости равно: , где S – путь, пройденный точкой за время .

Если в течение рассматриваемого промежутка времени скорость точки не изменяется по направлению, то

,

где x(t₁) и x(t₀) – координаты материальной точки в конечный и начальный моменты времени, соответственно.

В нашем случае в начальный момент времени с скорость точки равна 2 м/с, а в момент времени 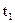скорость - . Следовательно, в некоторый момент времени скорость точки обращается в нуль, т.е. в этот момент времени материальная точка изменяет направление своего движения. Тогда весь путь, пройденный точкой, можно представить в ви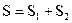де: , где - путь, пройденный точкой до остановки, а - путь, пройденный в обратном направлении.

Найдем момент времени, в который скорость точки равна нулю: .

Отсюда . Подставив численные значения, получим: =1,155 с.

Тогда =7,08 м,

=4 м,

Cледовательно, S=(7,08-4)+(7,08-4)=6,16 м, средняя скорость <v> =3,08 м/с.

Пример 2. Тело массой 10 кг движется вверх по наклонной плоскости. На тело действует сила F=100 Н, направленная вверх под углом = к поверхности наклонной плоскости. Коэффициент трения =0,1. Угол наклона плоскости = . Определить ускорение, с которым движется тело.

Решение

При движении тела кроме силы на него действуют также: сила тяжести - , сила реакции опоры - и сила трения - , показанные на рисунке.

Ускорение тела определим, используя основной закон динамики, который в векторной форме в условиях данной задачи имеет вид:

(1)

Направим ось X вдоль наклонной плоскости в сторону движения тела, а ось Y - перпендикулярно к ней.

Запишем уравнение (1) в проекциях на выбранные оси координат.

На ось X: (2)

на ось Y: (3)

По определению силы трения: .

Силу реакции опоры найдем из уравнения (3):

.

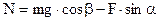Тогда .

Подставим это выражение в (2) и получим рабочую формулу: .

Проведя подстановку данных и вычисления, найдем: а=3,3м/с².

Пример 3. К ободу однородного диска радиусом 0,2 м, вращающегося вокруг своей оси, приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения Найти массу диска, если известно, что диск вращается с угловым ускорением =100 .

Решение

Известно, что момент инерции диска относительно оси, проходящей через его центр, равен: .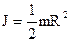

Отсюда масса диска: (1)

Воспользовавшись законом динамики вращательного движения твердого тела, найдем момент инерции J:

, (2)

где М - результирующий момент сил, под действием которого вращается диск. Запишем уравнение (2) в проекции на ось вращения (с учетом направлений моментов).

. (3)

Здесь – момент силы F относительно оси вращения.

Подставляя (2) и (3) в (1), находим:

.

Проведя необходимые расчеты, получим: m=7,36 кг.

Пример 4. Два свинцовых шара массами =2 кг и =3 кг подвешены на нитях длиной L=70 см. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на угол и отпустили. Считая удар центральным и неупругим, определить: 1) высоту h, на которую поднимутся шары после удара; 2) энергию , израсходованную на деформацию шаров при ударе.

Решение

Проведем анализ движения тел в данной задаче. Движение шаров можно разбить на три этапа.

На первом этапе (до соударения) шар массой m₁ движется под действием только консервативных сил (сила трения отсутствует). Следовательно, на этом участке движения выполняется закон сохранения механической энергии:

, (1)

где - начальная высота, на которой находился отклоненный шар, - скорость этого шара непосредственно перед ударом.

Второй этап – неупругое соударение шаров, при котором выполняется закон сохранения импульса:

,

где и - скорости шаров до удара, - скорость шаров, движущихся как единое целое, непосредственно после удара.

С учетом того, что , получим:

. (2)

Из уравнения (2) очевидно, что скорость шаров сразу после удара будет направлена вдоль оси Х, так же как и скорость первого шара непосредственно перед соударением. Поэтому, уравнение (2) в проекциях на ось Х будет иметь вид:

. (3)

На третьем этапе движения шаров после удара снова выполняется закон сохранения механической энергии:

. (4)

Отсюда искомая высота .

Используя уравнения (3) и (1), получим: ,

.

Тогда .

Энергия, израсходованная на деформацию шаров при ударе:

. (5)

Проведя подстановку и преобразования, получим:

.

Вычислим: 1) h=0,056 м; 2) =4,12 Дж.

Пример 5.Кинетическая энергия Е_к электрона равна . Определить скорость электрона, его релятивистские массу и импульс, а также полную энергию.