Решение. Кинетическая энергия релятивистской частицы равна:

Кинетическая энергия релятивистской частицы равна:

, (1)

где 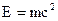- полная энергия, 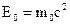- энергия покоя частицы (в нашем случае – электрона), кг - масса покоя электрона; - его релятивистская масса, , м/с - скорость света.

Последовательная подстановка этих величин в (1) приводит нас к формуле:

.

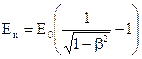Выполнив преобразования относительно , найдем скорость частицы, выраженную в долях скорости света :

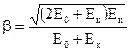. ( 2 )

Расчет энергии покоя дает величину:

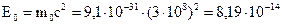(Дж).

Подставив числовые значения и Е_к в формулу (2), получим .

Так как , то получим: .

Найдем релятивистские массу m, импульс p и полную энергию Е:

кг,

Дж.

Пример 6. Материальная точка массой 5 г совершает гармонические колебания с частотой 0,5 Гц вдоль оси Х. Амплитуда колебаний 3 см. Определить: 1) скорость точки в момент времени, когда смещение х=1,5 см; 2) максимальную силу, действующую на точку.

Решение

1. Уравнение гармонического колебания имеет вид:

. (1)

По определению, скорость точки равна первой производной по времени от смещения:

. (2)

Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого возведем оба уравнения в квадрат:

, (3)

. (4)

Из уравнений (3) и (4) выразим , 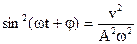. Воспользовавшись известным соотношением , получим:

.

Так как 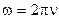, тогда

.

Решая последнее уравнение относительно v, найдем:

.

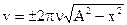Вычисляя, получим v=±8,2 м/с.

Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси Х, знак минус - когда направление скорости противоположно.

2. Силу, действующую на точку, найдем, используя второй закон Ньютона:

F = ma, (3)

где а - ускорение точки.

По определению:

или: .

Подставим это выражение в (3) и получим:

.

Отсюда максимальное значение силы

(при ):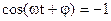

.

Подставим в это уравнение значения величин , , 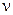m, А и найдем .

Пример 7.На концах тонкого стержня длиной 1 м и массой М=400г укреплены шарики малых размеров массами m₁=200 г и m₂=300 г. Стержень колеблется около горизонтальной оси, перпендикулярной стержню и проходящей через его середину (точка О на рис.). Определить период колебаний, совершаемых стержнем.

Решение

Период колебаний физического маятника, каковым является стержень с шариками, определяется соотношением:

, (1)

где J - момент инерции маятника относительно оси колебаний; m - его масса; а - расстояние от центра масс маятника до оси колебаний.

В силу аддитивности, момент инерции данного маятника равен сумме моментов инерции J₁ и J₂ шариков и стержня J₃:

J = J₁+J₂+J₃. (2)

Принимая шарики за материальные точки, запишем их моменты инерции: ; .

Так как ось проходит через середину стержня, то его момент инерции относительно этой оси . Подставив полученные выражения J₁, J₂ и J₃ в формулу (2), найдем общий момент инерции физического маятника:

.

Произведя вычисления по этой формуле, найдем J = 0,158 .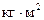

Масса маятника состоит из масс шариков и массы стержня:

m = m₁+m₂+М = 0,9 кг.

Расстояние от центра масс маятника до оси колебаний найдем, исходя из следующих соображений. Если ось Х направить вдоль стержня и начало координат совместить с точкой О, то искомое расстояние равно координате центра масс маятника , т.е.

,

или .

Подставив значения величин m₁, m₂, m, L и произведя вычисления, найдем: а= 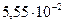м.

Произведя расчет по формуле (1), получим период колебаний физического маятника: Т=3,57 с.

Пример 8. В баллоне объемом 10 литров находится гелий под давлением 1 МПа при температуре 300 К. После того как из баллона был израсходован гелий массой 10 г, температура в баллоне понизилась до 290 К. Определить 1) давление гелия, оставшегося в баллоне; 2) его плотность; 3) количество оставшихся в баллоне молекул гелия; 4) их концентрацию.

Решение

1. Воспользуемся уравнением Менделеева – Клапейрона, применив его к начальному и конечному состояниям газа:

;

.

Выразим из этих уравнений массы m₁ и m₂ гелия и найдем их разность:

; .

.

Из последнего уравнения выразим искомое давление:

.

Молярная масса гелия (Не) равна 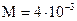кг/моль , R=8,31 Дж/(моль К) – молярная газовая постоянная.

Подставив данные и проведя расчет, найдем давление

=364 10³ Па.

2. Плотность вещества, по определению, равна . Выразим эту величину из исходного уравнения для второго состояния системы:

.

После подстановки данных и проведения расчета получим:

кг/м³.

3. Количество молекул, оставшихся в баллоне, равно: , где моль^-1 – число Авогадро. Количество вещества , оставшегося в баллоне газа, выразим из уравнения Менделеева – Клапейрона для второго состояния системы:

.

Тогда, искомое число молекул:

.

После подстановки данных и проведения расчета получим:

.

4. Концентрация молекул по определению равна: , тогда:

.

После подстановки данных и проведения расчета получим:

.

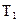Пример 9. Кислород, находящийся в состоянии 1 при давлении =0,5 МПа, температуре =350 К и занимающий объем 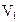=1л, перевели в состояние 2, подвергнув адиабатическому расширению до объема 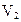=2 л. Затем изобарно объем газа был увеличен до =3 л. В состояние 4 кислород был переведен путем изотермического увеличения объема в два раза. После этого последовал изохорный нагрев на = 150К, который перевел газ в пятое состояние. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

Решение

Согласно первому началу термодинамики, количество теплоты Q, полученное газом, расходуется на изменение внутренней энергии газа ( ) и совершение газом работы (А) против внешних сил:

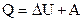. (1)

Параметры состояния 1 известны из условия задачи: =0,5 Па, = 1^.10 м , =350 К.

1. Адиабатный процесссовершается, по определению, без теплообмена с окружающей средой, и описывает, в рамках нашей задачи, переход системы из 1-го во 2-е состояние.

Поэтому: . (2)

Уравнение (1), записанное для адиабатного процесса, имеет вид: (3)

Известно, что изменение внутренней энергии для любого термодинамического процесса:

.

Тогда, в нашем случае:

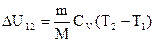, (4)

где m –масса газа, 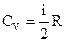- молярная теплоемкость при постоянном объеме, i=5 – число степеней свободы двухатомной молекулы, какой является молекула кислорода; R=8,31 Дж/(моль К) – молярная газовая постоянная; М = 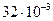кг/моль – молярная масса кислорода.

Температуру Т₂ найдем, используя уравнение Пуассона, описывающее адиабатный процесс:

,

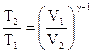где - показатель адиабаты.

Отсюда 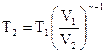. (5)

После подстановки исходных данных получим Т₂= 265 К.

Массу газа найдем из уравнения Менделеева – Клапейрона, записанного для состояния 1:

откуда 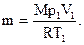(6)

Подстановка данных и расчет дает массу газа m=0,0055 кг.

Из уравнения Менделеева – Клапейрона для состояния 2 найдем давление р₂:

.

После подстановки в это уравнение выражения для массы (6) получим:

.

Подстановка данных и расчет приводят к результату р₂=0,189 Па.

Определили термодинамические параметры для состояния 2:

р₂=0,189 Па, V₂= 2^.10 м , T₂=265 К.

Подставив выражения для 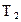, m и в уравнение (4), получим

. (7)

Подстановка в (7) численных значений приводит к результату:

Дж.

Из (3) следует: Дж.

Итак, для адиабатного процесса, переводящего систему из состояния 1 в состояние 2, получили: Дж, Дж, Дж.

2. Изобарный процессхарактеризуется постоянством давления. Для этого процесса первое начало термодинамики имеет вид:

.

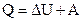При изобарном расширении (в нашей задаче это переход из состояния 2 в состояние 3) работа газа, по определению, равна:

, (8)

где р₂=0,189 Па=const. Из условия задачи известны V₂ и V₃. Подстановка численных значений в формулу (8) дает

А₂₃=189 Дж.

Температуру найдем, воспользовавшись законом Гей - Люссака для изобарного процесса: .

Отсюда: 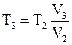=397 К.

Отметим, что так как процесс - изобарный, следовательно, р₂=р_3.

Определили термодинамические параметры для состояния 3:

Па, м , T₃=397 К.

Изменение внутренней энергии газа рассчитаем по уже известной формуле:

. (9)

Количество теплоты , полученное газом в изобарном процессе, найдем согласно (1):

(10)

Итак, для изобарного процесса, переводящего систему из состояния 2 в состояние 3, получили: A =189 Дж; 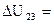471 Дж; =660 Дж.

3. Изотермический процессхарактеризуется постоянством температуры. Для этого процесса первое начало термодинамики имеет вид:

,

так как при постоянной температуре внутренняя энергия системы не изменяется, то есть .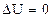

Следовательно, при изотермическом изменении объема (в нашей задаче это переход из состояния 3 в состояние 4) количество полученной газом теплоты будет совпадать с работой газа, которая, в свою очередь, равна:

. (11)

Определим параметры 4-го состояния: Т₄=Т₃, так как процесс - изотермический, V₄=2V₃ – по условию. Давление кислорода p₄ найдем из закона Бойля – Мариотта,:

.

Отсюда: . Подстановка числовых данных и расчет приводят к результату: p₄= Па.

Таким образом, термодинамические параметры 4 – го состояния: р₄= Па, V₄= 6^.10 м , T₄=397 К.

Теперь, когда известны все необходимые данные, проведем расчет по формуле (11) и получим: 393 Дж.

Для изотермического процесса, переводящего систему из состояния 3 в состояние 4, получили: A₃₄=393 Дж; 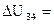0; Q₃₄=393 Дж.

4. Изохорный процесс. Характеризуется неизменностью объема, занимаемого газом. Так как, по определению, работа газом совершается только при изменении его объема, то для изохорного процесса она равна нулю. Это значит, что первое начало термодинамики имеет вид: .

Или, в наших обозначениях: .

Следовательно, при изохорном процессе количество подведенной к газу теплоты будет совпадать с изменением его внутренней энергии, которое, в свою очередь, равно:

. (12)

Определим параметры 5-го состояния: Т₅=Т₄+150=547 К – по условию задачи. Процесс - изохорный, следовательноV₅=V₄ =6^.10 м . Давление кислорода p₅ найдем из закона Шарля:

.

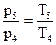Отсюда: 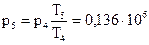Па.

Таким образом, термодинамические параметры 5 – го состояния: р₅=0,136 Па, V₅= 6^.10 м , T₄=547 К.

Проведя уже стандартный расчет по формуле (12) получим:

.

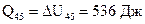Итак, для изохорного процесса, переводящего систему из состояния 4 в состояние 5, получили: A₄₅=0; 536 Дж; Q₄₅=536 Дж.

Пример 10. Определить изменение энтропии при изотермическом расширении кислорода массой 10 г от объема V₁=25 л до объема V₂=100 л.

Решение

По определению, изменение энтропии при переходе системы из состояния 1 в состояние 2 равно:

.

Найдем этот интеграл с учетом того, что по условию задачи процесс протекал изотермически (T – const). Тогда

, (1)

где Q₁₂ - количество теплоты , полученное газом при переходе из состояния 1 в состояние 2. Определим его, используя первое начало термодинамики:

.

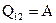Для изотермического процесса изменение внутренней энергии , следовательно, . (2)

Известно, что работа газа А при изотермическом расширении равна:

. (3)

С учетом (2) и (3) равенство (1) примет вид:

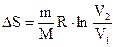. (4)

Подставив в (4) численные значения и произведя вычисления, получим:

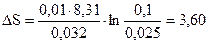Дж/К.