
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
МАТЕМАТИЧЕСКИЕ ДЕЙСТВИЯ С ОДНИМ РЕЗУЛЬТАТОМ ИЗМЕРЕНИЯ
Глава 10
ПЕРЕРАБОТКА ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
МАТЕМАТИЧЕСКИЕ ДЕЙСТВИЯ С ОДНИМ РЕЗУЛЬТАТОМ ИЗМЕРЕНИЯ
При математических действиях над результатами измерений нужно учитывать, что последние являются случайными значениями измеренных величин.Обращение с результатами измерений как с неслучайными значениями приводит к ошибкам. Некоторые из них будут рассмотрены на конкретных примерах.
Начнем с умножения результата измерения на постоянный множитель.
 |
Пример 84. Удвоить результат измерения r, эмпирическое распределение вероятности числового значения которого представлено табл. 54.
Таблица 54
| r | m | Р |
| 0,2 | ||
| 0,5 | ||
| 0,3 |
Решение. Результатом умножения случайного числа r на 2 будет новое случайное число 2r, распределение вероятности которого
2r P
6 0,2
8 0,5
10 0,3
Графически оно показано на рис 194. Вероятность удвоенных по сравнению с r значений остается прежней. Оценки числовых характеристик теоретической модели эмпирического распределения вероятности, представленного табл. 54,


так как нет никаких оснований полагать, что результат измерения подчиняется нормальному закону распределения вероятности. Оценки числовых характеристик теоретической модели нового случайного числа

следовательно,

Таким образом, для оценок справедливы свойства самих числовых характеристик (см. п. 2.2): среднее арифметическое произведение постоянного множителя а и результата измерения А равно произведению постоянного множителя и среднего арифметического результата измерения, то есть, если

В равной мере стандартное отклонение произведения постоянного множителя а и результата измерения А равно произведению модуля постоянного множителя и стандартного отклонения результата измерения:
SQ = |a| SA .
Теперь рассмотрим операцию возведения результата измерения в квадрат. Под квадратом результата измерения А понимается случайная величина
Q=A2 ,
которая с вероятностями Pi , соответствующими значениям Ai , принимает значения, равные Qi .
Пример 85. Возвести в квадрат результат измерения, рассмотренный в предыдущем примере.
Решение. Распределение вероятности числовых значений r2 выглядит следующим образом:
r2 Р
9 0,2
10 0,5
25 0,3
Оценки числовых характеристик теоретической модели этого распределения вероятности
 = 17,3; Sr2 = 5,7.
= 17,3; Sr2 = 5,7.
Пример 86. Определить площадь круга, распределение вероятности числовых значений радиуса которого представлено табл. 54.
Решение. Распределение вероятности числовых значений площади круга s = pr2 получаем, используя табл. 54:
s Р
28,3 0,2
50,3 0,5
78,5 0,3
Оценки числовых характеристик теоретической модели этого распределения вероятности

 = 54,4; SS= 17,7.
= 54,4; SS= 17,7.
Стандартное отклонение среднего арифметического значения площади круга
S  = 1,8.
= 1,8.
Так как закон распределения вероятности –s^ неизвестен, то на основании неравенства П.Л. Чебышева с вероятностью, больше чем 0,9 ,
 - 3,2 S
- 3,2 S  < s <
< s <  + 3,2 S
+ 3,2 S  .
.
Отсюда с вероятностью не менее 0,9
s = 48,7 . . . 60,1.
Рассмотренные примеры показывают, что при функциональном преобразовании результата измерения
Q = f(A) (54)
происходит трансформация его эмпирического закона распределения вероятности в соответствии с правилом
P(Qi )=P(Ai ).
Если результат измерения А задан теоретической моделью эмпирического закона распределения вероятности, то используется то, что интегральная функция распределения вероятности F(Q) представляет собой вероятность того, что
f(A) < Q.
Решение этого неравенства относительно А устанавливает пределы, в которых находится А с той же вероятностью.
Последняя равна интегралу от плотности распределения вероятности pA (A) в установленных пределах.
Пример 87. Определить трансформацию плотности распределения вероятности pA (A) результата измерения A после линейного преобразования Q = а А + b.
Решение.1.F(Q) = P{aA + b < Q}.
2. С вероятностью F(Q) результат измерения

3. После перестановки пределов в последнем интеграле и дифференцирования получаем:

Таким образом, как это можно было заметить еще на примере 84, при линейном преобразовании результата измерения распределение вероятности не меняется, а происходит только его смещение по оси абсцисс и компрессия либо декомпрессия.
Результат, полученный в примере 87, применительно к любоймонотонной функции (54) обобщается следующим образом:

где f -1 — функция, обратная функции f. В примере 87
Q - b
f -1 = ———— . Если f -1 —многозначная функция, то это отражается на
a
пределах, в которых находится А с вероятностью F(Q).
Пример 88. Определить трансформацию нормированного нормального закона распределений вероятности, которому подчиняется результат измерения A, после нелинейного преобразования Q = А 2 .
Решение. 1. F (Q) = Р {А2 < Q}.
2. Пределы, в которых выполняется неравенство, устанавливаются функцией A = ±  , обратной возведению A в квадрат (рис. 195). Поэтому
, обратной возведению A в квадрат (рис. 195). Поэтому

3. После дифференцирования получаем:

Для сравнения графики плотности исходного и преобразованного распределения вероятности показаны на рис. 196.

На практике преобразованиями законов распределения вероятности результатов измерений интересуются сравнительно редко. Обычно ограничиваются расчетами на уровне оценок числовых характеристик законов распределений.
Пример 89. По данным примера 84 определить числовое значение длины окружности l с радиусом r .
Решение.1.  = 2
= 2 
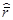 = 25,7; Sl= 2
= 25,7; Sl= 2  Sr = 4,4.
Sr = 4,4.
2. Стандартное отклонение среднего арифметического значения длины окружности
S  = Sl /
= Sl /  = 0,44.
= 0,44.
3. Согласно неравенству П.Л. Чебышева с вероятностью не менее 0,9
1=24,3 . . . 27,1.
Дата добавления: 2015-02-10; просмотров: 247; Мы поможем в написании вашей работы!; Нарушение авторских прав |