РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ, СОДЕРЖАЩИХ РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ

Наиболее общим случаем функционального преобразова­ния результатов измерений является преобразование одной многомерной величины, изображаемой точкой с координатами А, В, С, ... в n-мерном пространстве в другую многомерную величину Q, изображаемую точкой с координатами Q₁, Q₂,…,Q_m в т -мерном пространстве. Результаты измерений А, В, С, ... образуют одну систему случайных значений, а коорди­наты Q₁ ,Q₂ ,..., Q_m — другую, причем т п.

Многомерная интегральная функция распределения веро­ятности системы случайных значений F(Q₁,Q₂,...,Q_m) в рассматриваемом случае представляет собой вероятность то­го, что

f₁(A,B,C, ...) < Q₁;

f₂(А,В,С,…) < Q₂;

……………………

f_m(A,B,C,…) < Q_m .

Совокупность этих неравенств определяет некоторую область G в т -мерном пространстве, причем ни одно из неравенств не нарушается, если точки с координатами А, В, С, . . . находятся в пределах этой области. Вероятность последнего

F(Q₁,Q₂,…,Q_m ) = ò …_G ò p (A,B,C,…) dA dB dC … .

Если результаты измерений независимы, то

F(Q₁,Q₂,…,Q_m) = ò …_G ò p_A (A) p_B (B) p_C (C) … dA dB dC … .

Плотность распределения вероятности системы случайных значений

На практике иногда представляет интерес вероятностно-статистическое описание каждого из значений Q₁, Q₂,…, Q_m в отдельности. Эта задача решается путем интегрирования F (Q₁,Q₂,…,Qm ) по остальным переменным. В то же время, преобразование одной системы случайных значений (А, В, С, . . .) в другую (Q₁,Q₂,…,Q_m) может быть представле­носовокупностью уравнений

f₁ (А,В,С,...) =Q₁;

f₂ (А,В,С,...) =Q₂;

……………………

f_m (A,B,C,…) =Q_m .

не предполагающей их совместного решения. Каждое из этих уравнений, называемых совокупными, решается методами, рассмотренными в разд. 10.2.

Если совокупные уравнения являютсялинейными, то пре­образование одной системы случайных значений в другую мо­жет быть представлено в матричной форме, например,

где d_{i j} — коэффициенты в совокупных уравнениях.

Принципиально другим является случай, когда требуется определить значения Q₁,Q₂,… Q_m , связанные со значениями А, В, .... определяемыми посредством измерений, системой линейных уравнений

предполагающей их совместное решение. После подстановки в эти уравнения, называемые совместными, полученных эк­спериментально значений , . . . они принимают вид:

где знак равенства носит уже чисто условный характер, т.к. коэффициенты, входящие в эти уравнения, выражены через результаты измерений, не равные в точности значениям А, В, ... . Поэтому эти уравнения называются условными. Идея их решения методом наименьших квадратов принадле­жит Гауссу.

Если в условные уравнения ввести поправки Q_i , обраща­ющие их в строгие тождества и называемые в данном случяе невязками, то метод наименьших квадратов будет состо­ять в том, чтобы найти такие оценки значе­ний Q₁, Q₂ ,…, Q_m при которых сумма квадратов невязок была бы минимальной, т.е. в уравнениях

величины Q_i удовлетворяли бы условию

то требование минимизации суммы квадратов невязок можно записать следующим образом * :

* Eсли условные уравнения неравноценны, то каждое из них берет­ся со своим весом g . В этом случае минимизируется

Порядок дальнейших расчетов не меняется.

Веса условных уравнений выбираются обратно пропорциональны­ми их дисперсиям, но так, чтобы

n

Функция нескольких переменных S f ²_i достигает минимума

i =1

в точке, где все ее частные производные равны нулю. Поэто­му оценки интересующих нас значений находятся в резуль­тате решения системы уравнений

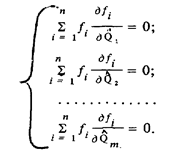
Обозначим коэффициенты при неизвестных в условных уравнениях через q_{i j} а свободный член через l _i . Тогда послед­ние уравнения можно будет представить в виде:

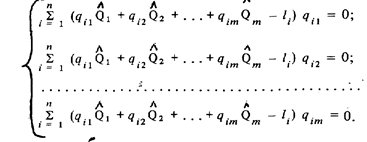
Раскрыв в них скобки, получим систему так называемых нормальных уравнений

которая будет более обозримой, если суммирование по i обоз­начить квадратными скобками. При таком обозначении, вве­денном Гауссом,

Число нормальных уравнений равно числу неизвестных, так что эта система имеет обычное решение:

где главный определитель (детерминант) системы

а определители D₁, D₂, …, D_m получаются из главного оп­ределителя D путем замены столбца, составленного из коэф­фициентов при неизвестном 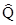_j столбцом, составленным из свободных членов, например,

Стандартные отклонения оценок выража­ются через невязки и коэффициенты в условных уравнениях следующим образом:

где D_jj — миноры (алгебраические дополнения) элементов [q₁q₁] , [q₂q₂] , … , [q_mq_m] главного определителя сис­темы D, т.е. определители (т — 1)-го порядка, получаю­щиеся путем вычеркивания в главном определителе j-и строки и j-го столбца.

Пределы, в которых находятся значения Q₁, Q₂, …, Q_m определяют либо исходя из того, что подчи­няются закону распределения вероятности Стьюдента (вмес­то п на рис. 38 используется в этом случае значение п - т), либо с помощью неравенства П.Л. Чебышева.

Пример 98. В соответствии со 2-м, 4-м и 9-м вариантами, представ­ленными в табл. 58, при четырех взвешиваниях были получены следую­щие значения: m_б = 3,98 кг; т_Т = 0,9 кг; m_б – т_T = 3,12 кг; m_б + т_Т = 4,96 кг. Определить m_б и m_T методом наименьших квадратов.

Решение. 1. Для числовых значений исходная система условных упавнении имеет вид:

2. Если эти условные уравнения равноценные, то, вводя невязки и переходя к оценкам, которые нужно будет найти из условия миними­зации суммы квадратов невязок, получим:

3. Суммирование произведений каждой функции f_i, на ее производ­ную по первой переменной ( 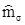) дает

Таким образом, система нормальных уравнений имеет вид:

4. Каждое из полученных нормальных уравнений дает значение одной из искомых оценок, но, следуя общей схеме расчетов, напишем

7. На основании неравенства П.Л. Чебышева с вероятностью не ме­нее 0,9

8. Рассмотрим теперь случаи, когда заранее известно, что точность взвешивания тары примерно в 1,6 раза выше, чем консервированного продукта брутто:

Ценность второго условного уравнения тогда больше, чем первого. Если учитывать ценность условных уравнений весовыми коэффици­ентами. обратно ггсюпооциональными их дисперсиям, то

так как дисперсии третьего и четвертого условных уравнении равны сум­ме двух первых, а сумма всех весовых коэффициентов должна равнять­ся единице.

9. Суммирование умноженных на g²_i произведении каждой функции f_i на ее производную по первой переменной ( 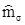) теперь даст

Таким образом, система нормальных уравнений:

СПИСОК ЛИТЕРАТУРЫ

1. Маликов М.Ф. Основы метрологии. — М.: Комитет по делам мер и измерительных приборов, 1949.

2. Бурдун Г.Д., Марков Б.Н. Основы метрологии: Учеб. пособие.— 3-е изд., перераб. и доп. — М.: Изд-во стандартов, 1984.

3. Тюрин Н.И. Введение в метрологию: Учеб. пособие,— 3-е изд. перераб. и доп.— М.: Изд-во стандартов, 1985.

4. Спортивная метрология / Под ред. В.М. Зарицкого. — М.: Физ­культура и спорт,1982.

5. Шишкин И.Ф. Основы метрологии, стандартизации и контроля качества: Учеб. пособие.— М.: Изд-во стандартов, 1988.

6. Сена Л.А. Единицы физических величин и их размерность. — М.: Наука, 1977.

7. Карасев А.И. Основы математической статистики. — М.: Росвуз-издат, 1962.

8. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и ма­тематической обработки результатов опыта. — М.: Физматгиз, 1962.

9. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. — М.:

Наука, 1965.

10. Зайдель А.Н. Элементарные оценки ошибок измерении: — Л.:

Наука, 1968.

11. Румшинский Л.3. Математическая обработка результатов эк­сперимента.— М.: Наука, 1971.

12. Долинский Е.Ф. Погрешности измерений и обработка резуль­татов измерения. — М.: Машиностроение, 1967.

13. Долинский Е.Ф. Обработка результатов измерения. — М.: Иэд-во стандартов, 1973.

14. Фрумкин В.Д., Рубичев Н.А. Теория вероятностей и статисти­ка в метрологии и измерительной технике. — М.: Машиностроение, 1987.

15. Тойберт П. Оценка точности результатов измерений: Пер. с нем.—М.: Энергоатомиздат, 1988.

16. Чарьгков А.К. Математическая обработка результатов хими­ческого анализа: Учеб. пособие для вузов. — Л.: Химия, 1984.

17. Семенов Л.А., Сирая Т.Н. Методы построения градуировочных характеристик средств измерений.— М.: Изд-во стадартов, 1986.

18. Куликов Е.И. Методы измерения случайных процессов. — М.:

Радио и связь, 1986.

19. Соболев В.И. Информационно-статистическая теория измерений. Учебник для вузов. — М.: Машиностроение, 1983.

20. Цветков Э.И. Основы теории статистических измерений. — Л.:

Энергия, 1979.

21. Ширман Я.Д., Голиков В.Н. Основы теории обнаружения радио­локационных сигналов и измерения их параметров.—М.:Сов. радио, 1963.

22. Клюев Н.И. Информационные основы передачи сообщений. — М.: Сов.радио,1966.

23. Хармут Х.Ф. Передача информации иртогональными функция­ми: Пер. с англ.— М.: Связь, 1975.

24. Кончак B.C., Пойда В.Н., Садыхов Р.Х., Чеголин П.М. Класс нестационарных процессов, инвариантных к спектру Уолта// VII Все­союзный симпозиум "Методы-представления и аппаратурный анализ случайных процессов и полей".—Л.: ЭП, 1974.

25. Харкевич А.А. Спектры и анализ. — 4-е изд. — М.: Фиэматгиз,

26. Харкевич А.А. Борьба с помехами. — 2-е изд. — М.: Физматгиз, 1965. ,

27. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. — М.-г Л.: Энергия, 1965.

28. Снегирев В .Т., Бабкова Л.А. Линейные радиотехнические уст­ройства: Курс лекций: Ч. 1 / Под ред. проф. А.А. Ланнэ. — ВАС, 1981.

29. Дворяшин В.В., Кузнецов Л.И. Радиотехнические измерения:

Учеб. пособие для вузов. — М.: Сов. радио, 1978.

30. Кушнир Ф.В. Электрорадиоизмерения: Учеб. пособие для вузов.

—Л.: Энергоатомиздат, 1983.

31. Кукуш В.Д. Электрорадиоизмерения: Учеб. пособие для вузов.— М.: Радио и связь, 1985.

32. Елизаров А.С. Электрорадиоизмерения: Учеб. пособие для вузов.

—Минск.: Вышэйшая школа, 1986.

33. Куликовский К.Л., Купер В.Я. Методы и средства измерений:

Учеб. пособие для вузов.—М.: Энергоатомиздат, 1986.

34. Шляндин В.М. Цифровые измерительные устройства: Учебник для вузов. — 2-е изд., перераб. и доп. — М.: Высш. школа, 1981.

35. Боднер В.А. Приборы первичной информации: Учебник для авиационных вузов.— М.: Машиностроение, 1981.

36. Боднер В.А., Алферов А.В. Измерительные приборы: Учебник для вузов: В 2 т. — М.: Изд-во стандартов, 1986.

37. Воронцов Л.Н., Корндорф С.Ф. Приборы автоматического кон­троля размеров в машиностроении: Учеб. пособие для вузов. — М.: Ма­шиностроение, 1988.

38. Митин В.В., Усков В.И., Смирнов Н.Н. Автоматика и автомати­зация производственных процессов мясной и молочной промышлен­ности: Учебник для вузов.— М.: ВО "Агропромиздат", 1987.

39. Якушев А.И„ Воронцов Л.Н., Федотов Н.М. Взаимозаменяемость, стандартизация и технические измерения: Учебник для втузов. — 6-е изд., переработ, и доп. — М.: Машиностроение, 1986.'

40. Данцер К., Тан. Э., Мольх Д. Аналитика: Системат. • обзор:

Пер. с нем. / Под ред. Клячко Ю.А. — М.: Химия, 1981.

41. Сретенский В.Н. Метрологическое обеспечение производства приборов микроэлектроники.— М.: Радио и связь, 1988.

42. Азгальдов Г.Г., Райхман Э.П. О квалиметрии. — М.: Изд-во стандартов, 1973.

43. Азгальдов Г.Г. Потребительская стоимость и ее измерение. — М.: Экономика, 1971.

44. Райхман Э.П., Азгальдов Г.Г. Экспертные методы в оценке ка­чества товаров. — М.: Экономика, 1974.

45. Азгальдов Г.Г. Теория и практика оценки качества товаров (основы квалиметрии).— М.: Экономика, 1982.

46. Гличев А.В., Рабинович Г.0., Примаков Н.И., Синицын М.М. Прикладные вопросы квалиметрии. — М.: Изд-во стандартов, 1983.

47. Блюмберг В.А., Глущенко В.Ф. Какое решение лучше?: Метод расстановки приоритетов.— Л.: Лениздат, 1982.

48. Аристов О.В., Мишин В.М. Качество продукции: Учеб. пособие.

—М.: Изд-во стандартов, 1982.