ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ

Граф – это совокупность двух множеств: множества точек, которые называются вершинами, и множества ребер А. Каждый элемент есть упорядоченная пара элементов множества , вершины и называются концевыми точками или концами ребра а. Граф называется конечным, если множества R и конечны.

Это определение графа должно быть дополнено в одном важном отношении. В определении ребра можно принимать или не принимать во внимание порядок расположения двух его концов. Если этот порядок несущественен, т. е. если , то говорят, что a есть неориентированное ребро; если же этот порядок существенен, то a называется ориентированным ребром (ориентированное ребро часто называется дугой). В последнем случае называется также начальной вершиной, а – конечной вершиной ребраa. Граф называется неориентированным, если каждое его ребро не ориентировано, и ориентированным, если ориентированы все его ребра. В ряде случаев естественно рассматривать смешанные графы, имеющие как ориентированные, так и неориентированные ребра.

Ребра, имеющие одинаковые концевые вершины, называются параллельными. Ребро, концевые вершины которого совпадают, называется петлей. Она обычно считается неориентированной. Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой. Вершина, не инцидентная никакому ребру, называется изолированной. Граф, состоящий только из изолированных вершин, называется нуль-графом. Две вершины, являющиеся концевыми для некоторого ребра называются смежными вершинами. Два ребра, инцидентные одной и той же вершине, называются смежными.

Число ребер, инцидентных одной вершине , будем обозначать через . Это число называется локальной степенью или просто степенью графа в вершине . В случае ориентированного графа G обозначим через и число ребер, соответственно выходящих из вершины и входящих в . Эти числа называются локальными степенями G в . Если все числа конечны, то граф называется локально-конечным. Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной.

Рисунок 1.

На рис. 1 и – параллельные ребра, – петля; вершина и ребро инцидентны друг другу; – смежные вершины, – смежные вершины; степень вершины равна трем, – висячая вершина, – изолированная.

Теорема 1. В графе G сумма степеней всех его вершин – число четное, равное удвоенному числу ребер графа: , где n – число вершин графа, m – число его ребер.

Теорема 2. Число нечетных вершин любого графа, т. е. вершин, имеющих нечетную степень, четно.

Граф G называется полным, если любые две его различные вершины соединены ребром и он не содержит параллельных ребер. Дополнением графа G называется граф с теми же вершинами, что и граф G и содержащий только те ребра, которые нужно добавить к графу G, чтобы получился полный граф. Граф G называется плоским, если он может быть изображен на плоскости так, что все пересечения ребер являются его вершинами.

Рисунок 2.

На рис. 2 изображены следующие графы: 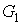– полный граф с пятью вершинами, – некоторый граф, имеющий пять вершин, –дополнение графа .