ЭЙЛЕРОВЫ И ГАМИЛЬТОНОВЫ ГРАФЫ

Эйлеровым циклом (путем) графа называется цикл (путь), содержащий все ребра графа ровно один раз. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.

Теорема 4. Граф G обладает эйлеровым циклом с концами 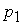и тогда и только тогда, когда G – связный и 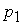, – единственные его вершины нечетной степени.

Теорема 5. Граф G является эйлеровым тогда и только тогда, когда G – связный и все его вершины имеют четную степень.

Гамильтоновым циклом (путем) графа G называется цикл (путь), проходящий через каждую вершину G в точности по одному разу. Граф, обладающий гамильтоновым циклом, называется гамильтоновым. Критерий существования гамильтонова цикла в произвольном графе G еще не найден. Достаточным условием существования гамильтонова цикла является полнота графа G.

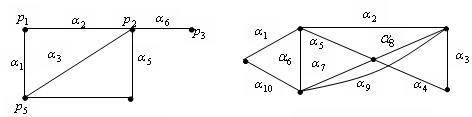
Рисунок 5. Рисунок 6.

На рис. 5 граф G не является эйлеровым (вершина инцидентна только одному ребру) и не является гамильтоновым, но обладает эйлеровым путем с концевыми вершинами и . Граф изображенный на рис. 6 является эйлеровым (последовательность ребер 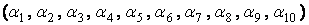образует эйлеров цикл).