
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение аналитической кривой
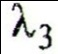
 . Находим значение второй и третьей статистик ( , ) по формулам :
. Находим значение второй и третьей статистик ( , ) по формулам :


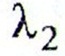 = -0,390/(30-1)= - 0,013
= -0,390/(30-1)= - 0,013
= 0,427/(30-1) = 0,015
Далее из приложения 5 мы ищем номограмму соответствующую нашим значениям. Для данных расчётов нам подошла номограмма на стр
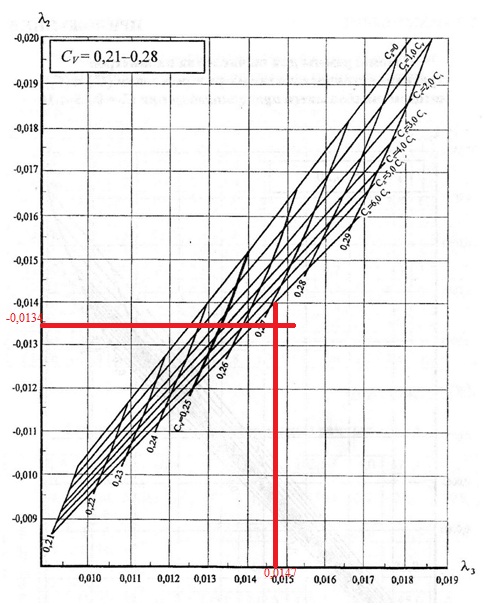
Проведя перпендикуляры, находим точку пересечения. Видим что она ближе всего к значению коэффициента вариации C v = 0,27 и к прямой соотношения Cs=6C v .
По таблице на странице (прибегая к методу интерполяции) находим значения pi и Ki.
Метод интерполяции:
Наносим на шкалу значения Cv наиболее близкие к полученному значению.
В нашем случае это 0, 2 и 0,3. Разбиваем шкалу на 10 равных частей и наносим наше значение 0,27.
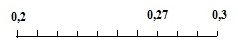
Далее составляем ещё одну шкалу и наносим значения Ki при 0,1 для Cv равное 0,2 и 0,3 (приложение ).

Находим Ki для pi= 0,27.
Ki=(2,8-2,02)/10*7= 2,566
По такой же схеме вычисляются значения Ki для каждого pi.
НО !
Метод интерполяции достаточно трудоёмок, и поэтому для облегчения задачи при вычислении Cv его округляют до одного знака после запятой.
В нашем случае 0,27 округляем до 0,3.
Заполняем таблицу 1.2 для построения аналитической прямой из приложения.
табл. 1.2
| Pi, % | Ki |
| 0,1 | 2,8 |
| 0,5 | 2,22 |
| 1,0 | 2,01 |
| 3,0 | 1,68 |
| 5,0 | 1,55 |
| 10,0 | 1,37 |
| 20,0 | 1,19 |
| 30,0 | 1,06 |
| 40,0 | 1,01 |
| 50,0 | 0,94 |
| 60,0 | 0,88 |
| 70,0 | 0,83 |
| 80,0 | 0,77 |
| 90,0 | 0,7 |
| 95,0 | 0,65 |
| 97,0 | 0,62 |
| 99,0 | 0,57 |
| 99,9 | 0,5 |
Чертим аналитическую кривую по значениям таблицы 1.2 и размещаем её на одном графике с эмпирической кривой.(гр. №2)
гр. 2
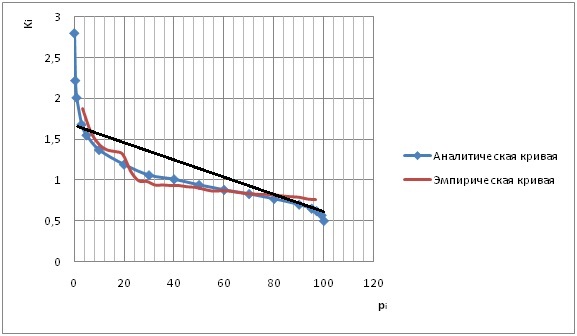
Необходимо убедиться, что не осталось резко отклоняющихся точек, свидетельствующих о неоднородности соответствующих членов.
Проведя прямую линейной зависимости двух функций, видим что кривые располагаются достаточно близко к ней.
Дата добавления: 2015-02-10; просмотров: 300; Мы поможем в написании вашей работы!; Нарушение авторских прав |