
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВЕРОЯТНОСТАЯ ОЦЕНКА УЩЕРБА ПРИ ЧС
Независимо от характера и источника ЧС вероятность определенной степени разрешений и поражения людей можно выразить с помощью одного и того же соотношения:
 , (2.1)
, (2.1)
где  -функция Лапласа,
-функция Лапласа,  - пробит функция. Выражение для пробит функции, включающие количественные характеристики поражающих факторов, найдены для всех основных опасных событий путем обработки статистических данных о последствиях аварий и катастроф.
- пробит функция. Выражение для пробит функции, включающие количественные характеристики поражающих факторов, найдены для всех основных опасных событий путем обработки статистических данных о последствиях аварий и катастроф.
Значение функции Лапласа могут быть найдены по таблицам или вычислить с помощью приближенной формулы:
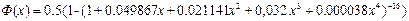
(2.2) При вычислениях по формуле (2.1)следует иметь в виду свойства функции Лапласа:
 =
= 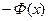 ;
; 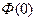 =0;
=0;  (2.3)
(2.3)
Из формулы (2.1) следует, чего при  2.33 вероятность заданного разрушения или поражения человека превышает 99%, т.е. заданный ущерб становится практически достоверным.
2.33 вероятность заданного разрушения или поражения человека превышает 99%, т.е. заданный ущерб становится практически достоверным.
При  =
=  3.2,
3.2,  и вероятностью поражения можно пренебречь.
и вероятностью поражения можно пренебречь.
Например, одним из поражающих факторов пожара, является тепловое излучение.
Пробит-функция для оценки вероятности смертельных поражений людей в результате их теплового облучения имеет вид:
 =-14,5+2.56ln(
=-14,5+2.56ln( 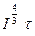 ), (2.4)
), (2.4)
где I-интенсивность воздействующего на человека теплового потока, кВт/ 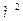 ;
;
 -время воздействия, с.
-время воздействия, с.
Подставив в формулу (2.4) 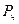 =2.33 и
=2.33 и 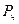 =0.025, найдем значения выражения
=0.025, найдем значения выражения 
для критического и безопасного состояния незащищенного человека в зоне действия теплового потока
 ,
,
 . (2.5)
. (2.5)
Для оценки критического (  ), также безопасного (
), также безопасного (  ) расстояния от источника теплового излучения можно воспользоваться формулой:
) расстояния от источника теплового излучения можно воспользоваться формулой:
 кВт/
кВт/ 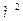 , (2.6)
, (2.6)
где  - абсолютная температура источника излучения, К (Т=273+t c);
- абсолютная температура источника излучения, К (Т=273+t c);  -площадь источника излучения,
-площадь источника излучения, 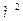 ;
; 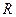 -расстояние, м.
-расстояние, м.
Для интерполяции результатов расчетов по формулам (2.1-2.6) можно использовать интерполяционную формулу Лагранжа второй степени:
 (2.7)
(2.7)
При применении этой формулы необходимо следить за тем, что бы одни из разностей  ,
, 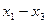 ,
,  не была очень малой.
не была очень малой.
Дата добавления: 2015-02-10; просмотров: 222; Мы поможем в написании вашей работы!; Нарушение авторских прав |