Вычислить приближенное значение суммы ряда c точностью

Ε=10^–6 для значений t є [ t₀ ; t₁ ] с шагом Dt , где t₀ = 0,2; t₁ = 0,7; Dt = 0,05;

p – среднее геометрическое элементов матрицы А,удовлетворяющих условию a_ij > 1 и ; r – минимальный по модулю элемент матрицы А; k₁ , k₂ – номера строки и столбца максимального из элементов матрицы А, удовлетворяющих условию а_ij < 3 ;

№27

Вычислить приближенное значение суммы ряда 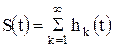c точностью

Ε=10^–5 для значений t є [ t₀ ; t₁ ] с шагом Dt , где t₀ = 0,4; t₁ = 0,9; Dt = 0,05;

p – максимальный элемент матрицы С=А*В; r – среднее арифметрическое положительных элементов матрицы С; k₁ , k₂ – номера строки и столбца минимального из элементов матрицы С, лежащих ниже главной диагонали;

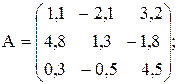
№28

Вычислить приближенное значение суммы ряда c точностью

Ε=10^–6 для значений t є [ t₀ ; t₁ ] с шагом Dt , где t₀ = 0,4; t₁ = 0,8; Dt = 0,04;

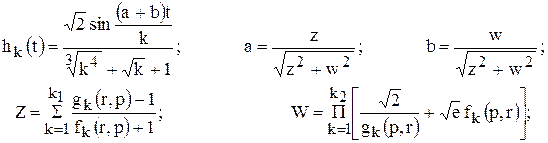
p – максимальный элемент вектора y=A*B; r – длина вектора y; k₁ , k₂ – минимальный из элементов матрицы А, удовлетворяющих условию 1 < а_ij < 3 ;

; ;

№29

Вычислить приближенное значение суммы ряда 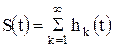c точностью

Ε=10^–5 для значений t є [ t₀ ; t₁ ] с шагом Dt , где t₀ = 0,5; t₁ = 0,9; Dt = 0,04;

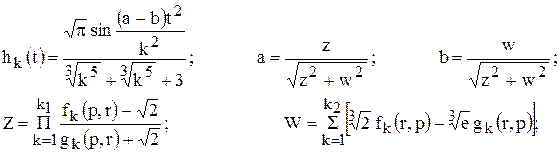
p – скалярное произведение вектора , соствленного из минимальных элементов строк матрицы А, на тот же вектор , но упорядоченый по возростанию; r – максимальный из элементов матрицы А, удовлетворяющих условию | а_ij | < 2 ;

k₁ , k₂ – номера строки и столбца этого элемента;

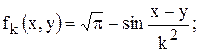
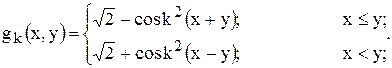
№30