ОРГАНИЗАЦИЯ ПРОГРАММ, СОДЕРЖАЩИХ ФУНКЦИИ ПОЛЬЗОВАТЕЛЯ

Задание 10

Составить программу вычисления функции W, используя функции пользователя.

Варианты задания

Вар.	Функции	Функции пользователя
1.		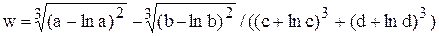y = x+lnx
2.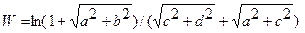
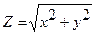
3.
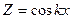
4.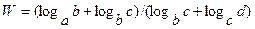
5.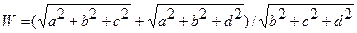
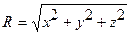
6.
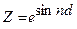
7.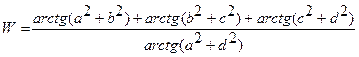
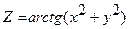
8.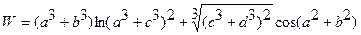
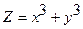
9.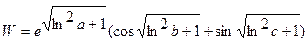
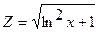
10.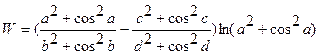
11.
12.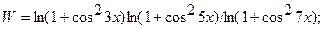
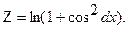
13.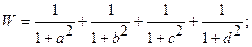
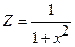
14.
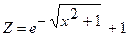
15.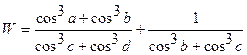
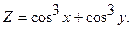
16.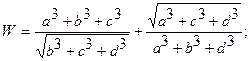
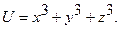
17.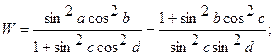
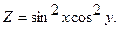
18.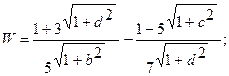
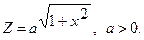
19.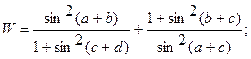
20.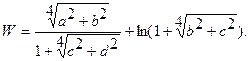
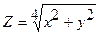
21.
22.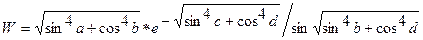
23.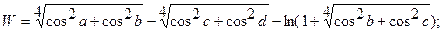
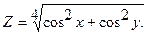
24.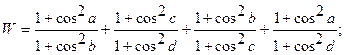
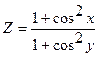
25.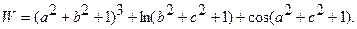
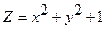
26.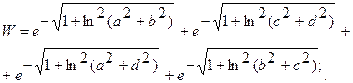
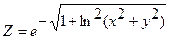
27.
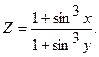
28.
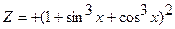
29.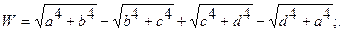
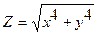
30.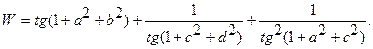

ОРГАНИЗАЦИЯ ПРОГРАММ, СОДЕРЖАЩИХ ПОДПРОГРАММЫ ПОЛЬЗОВАТЕЛЯ

Задание 11

Составить схему алгоритма и программу вычисления значения функции z с использованием подпрограмм. Вывести значения p,r,z.

Варианты задания

№1

Вычислить значение функции z= , где р – максимальный элемент среди элементов вектора х, удовлетворяющих условию х_i < 1; r – длина вектора x;

x = {-0,3; 2,5; 0,7; -3,1; 4,5; -0,1}

№2

Вычислить значение функции z= 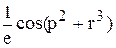, р – среднее арифметическое элементов вектора х, удовлетворяющих условию ½x_i½ < 2;

r – скалярное произведение вектора х на єтот же вектор, но упорядоченій по возростанию;

x = {-0,3; 2,5; -3,1; 4,8; -0,1; 7,5; 0,9}

№3

Вычислить значение функции z= 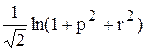, где р – скалярное произведение вектора х на этот же вектор, но упорядоченый по убыванию; r – среднее геометрическое положительных элементов вектора х;

x = {3,2; -0,1; 2,8; -0,2; 4,5; -0,4}

№4

Вычислить значение функции z= 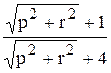, где р – среднее арифметическое элементов вектора х, удовлетворяющих условию –1 < x_i < 2;

r - минимальный элемент среди положительных элементов вектора х;

x = {0,7; -0,3; 2,5; 1,1; 3,4; -0,3; 0,9; -2,1}

№5

Вычислить значение функции z= , где р –максимальный элемент среди отрицательных элементов вектора х; r – произведение отрицательных элементов вектора х;

x = {-1,3; 4,5; 0,9; -0,4; 1,1; 1,9; -0,9; 7,1}

№6

Вычислить значение функции z= , где р – среднее арифметическое отрицательных элементов вектора х, удовлетворяющих условию –1 < x_i < 2;

x = {0,3; 4,2; -0,9; 7,2; -0,7; -1,3; 2,5}

№7

Вычислить значение функции z= , где р – среднее арифметическое элементов вектора х, удовлетворяющих условию x_i < 2 или x_i > 3; r – длина вектора, составленного из этих элементов, упорядоченого по убыванию;

x = {2,2; -0,4; 3,5; 6,1; 2,5; -2,9; 2,1}

№8

Вычислить значение функции z= , где р – среднее геометрическое модулей элементов вектора х, удовлетворяющих условию ½x_i½>3; r – максимальный элемент среди элементов вектора х, удовлетворяющих условию x_i < 2;

x = {-1,2; 0,4; -0,1; 2,5; 4,5; -5,1}

№9

Вычислить значение функции z= 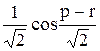, где р – скалярное произведение вектора х на этот же вектор, упорядоченый по возростанию;

r – минимальный элемент среди элементов вектора х; удовлетворяющий условию –1 < x_i < 2

x = {0,5; 4,2; -0,3; 4,5; 0,6; 1,5; -6,1}

№10

Вычислить значение функции z= 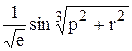, где р – длина вектора у, составленного из отрицательных элементов вектора х; r – скалярное произведение вектора у на этот же вектор но упорядоченый по убыванию;

x = {-0,3; 4,5; -1,2; 2,8; -3,1; -0,8; 2,1}

№11

Вычислить значение функции z= , где р – длина сумма отрицательных элементов вектора х; r – длина вектора у составленного из элементов вектора х, удовлетворяющих условию ½x_i½ < 0,5;

x = {-0,2; 3,1; -2,1; 0,7; 0,3; -0,4; 1,2}

№12

Вычислить значение функции z= , где р – произведение элементов вектора х, удовлетворяющих условию 1 < x_i < 3;

x = {-0,5; 4,5; 1,3; -2,1; 3,2; -1,5; 2,5; 1,6}

№13

Вычислить значение функции z= 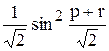, где р – скалярное произведение вектора х на этот же вектор, но упорядоченый по убыванию;

r – длина вектора х;

x = {0,4; -2,1; 3,1; -4,5; 2,8; -0,1; -6,2}

№14

Вычислить значение функции z= 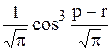, где р – максимальный элемент среди элементов вектора х, удовлетворяющих условию x_i < 1; r –среднее арифметическое отрицательных элементов вектора х;

x = {2,1; -1,5; 4,5; -0,1; 6,1; -3,1; 2,8; 1,3}

№15

Вычислить значение функции z= 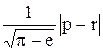, где р – максимальный элемент среди элементов вектора х, удовлетворяющих условию x_i < 2; r – длина вектора у, составленного из упорядоченных по возростанию отрицательных элементов вектора х;

x = {-1,5; 2,3; -6,1; 0,1; 3,5; -4,5; 2,8; -7,1}

№16

Вычислить значение функции z= 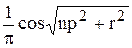, где р – среднее геометрическое модулей элементов вектора х, удовлетворяющих условию x_i > 1,5; n – число таких элементов; r – длина вектора у , составленного из положительных элементов вектора х;

x = {0,2; 4,5; -0,1; 6,2; -3,1; 1,1; 2,5; -1,3}

№17

Вычислить значение функции z= 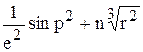, где р – максимальный элемент среди элементов вектора х, удовлетворяющих условию x_i < 3; r – среднее арифметическое элементов вектора х, удовлетворяющих условию ½x_i½ > 1; n – число таких элементов;

x = {2,8; -3,2; 5,1; 0,2; 6,3; -2,1; 2,1; 3,5}

№18

Вычислить значение функции z= 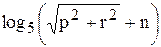, c на этот же вектор, но упорядоченый по убыванию; r – произведение отрицательных элементов вектора х; n –число таких элементов;

x = {-0,2; 3,1; -2,3; 5,2; -3,3; 6,1; -0,4; 2,1}

№19

Вычислить значение функции z= 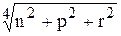, где р – среднее арифметическое элементов вектора х, удовлетворяющих условию ½x_i ½< 2;

r –длина вектора у, составленного из упорядоченых по возростанию элементов вектора х, удовлетворяющих условию x_i > 1;

x = {0,2; 4,5; -1,3; 2,8; -1,5; 3,2; 0,7; -1,1}

№20

Вычислить значение функции z= 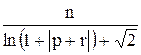, где р – минимальный элемент среди элементов вектора х, удовлетворяющих условию x_i < 3; n – число таких элементов; r – длина вектора у, составленых из упорядоченных по убыванию элементов вектора х, удовлетворяющих условию x_i < 2;

x = {1,5; -2,8; 5,2; -4,5; 2,3; 5,1; 1,7; -0,2}

№21

Вычислить значение функции z= 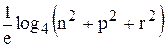,где р-среднее геометрическое модулей элементов вектора x , удовлетворяющих условию

-2< <I; n– число таких элементов ; ; n– число таких элементов; r– максимальный элемент среди элементов вектора x , удовлетворяющих условию x_i<2;

x = {-1,5; 2,8; 0,7; 3,1; -0,9; 1,6; 0,3; 4,1}.

№22

Вычислить значение функции z= 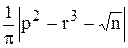, где p– длина вектора y,составленного из упорядоченных по убыванию элементов вектора x, удовлетворяющих условию 2< x_i <5 ; n– число таких элементов; r– максимальный элемент вектора х;

x = { 2,8; -3,5; 4,5; -1,6; 6,2; -0,1; 3,5}.

№23

Вычислить значение функции z= 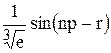,где p–скалярное произведение вектора y, составленного из упорядоченных по возростанию отрицательных элементов вектора х ,на тот же вектор y, но из упорядоченных по убыванию; z– длина вектора y; n– число элементов вектора y;

x = { 2,8; -3,5; 0,7; -2,3; 0,9; -1,1; 6,2; -3,8}.

№24

Вычислить значение функции z= 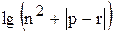, где р – среднее арифметическое элементов вектора х , удовлетворяющих условию | x_i | > 3 ; n– число таких элементов; r– максимальный элемент среди элементов вектора x , удовлетворяющих условию x_i < 1;

x = { 2,1; -3,5; 5,6; 0,7; -2,8; 6,3; -0,1}.

№25

Вычислить значение функции z= , где р – произведение элементов вектора х , удовлетворяющих условию 2< x_i <4 ; n– число таких элементов; z–элемент , минимальный среди них ;

x ={ 2,8; -0,3; 4,5; -0,8; 2,4; -0,7; 3,5; 3,2}.

№26

Вычислить значение функции z= 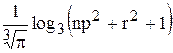,где р-среднее геометрическое элементов вектора x , удовлетворяющих условию x_i > 3; n– число таких элементов ; r – длина вектора у, составленых из упорядоченных по убыванию отрицательных элементов вектора х ;

x = { 2,3; -0,1; 3,5; -0,9; 2,1; -3,7; 4,2; -2,5; 6,1}.

№27

Вычислить значение функции z= 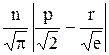, где p– длина вектора y,составленного из упорядоченных по убыванию элементов вектора x, удовлетворяющих условию |x_i |<2 ; n– число элементов вектора x ;

r–максимальный элемент вектора х;

x = { -0,5; 2,3; 1,2; 5,2; -3,1; 0,6; -1,7}.

№28

Вычислить значение функции z= 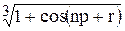, где р – минимальный элемент среди элементов вектора х, удовлетворяющих условию x_i > 3; n – число таких элементов; r – среднее арифметическое элементов вектора х, удовлетворяющих условию -1< x_i < 0,5;

x = { -0,8; 5,1; -0,3; 4,5; 0,2; 6,3; -0,9; 1,1}.

№29

Вычислить значение функции z= , где p– длина вектора y,составленного из упорядоченных по убыванию элементов вектора x, удовлетворяющих условию |x_i |>2 ; n– число элементов вектора y ; r – среднее геометрическое элементов вектора y, удовлетворяющих условию y_i < 5;

x = {2,1; -6,2; 3,5; 5,3; 0,7; 3,1; 4,5; -2,5}.

№30

Вычислить значение функции z= 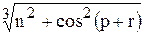, , где р – минимальный элемент среди элементов вектора х, удовлетворяющих условию x_i > 3; n – число таких элементов; r – среднее арифметическое элементов вектора х, удовлетворяющих условию x_i < 1 или x_i > 2 ;

x ={-0,1; 8,3; -1,5; 2,6; -4,5; 1,7; 3,6; 1,3; 4,5}.

Задание 12

Составить схему алгоритма и программу решения задачи с использованием полпрограмм пользователя. Вывестизначения p , r , y .

Варианты задания

№1

Вычислить значение функции y= 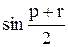, где p – максимальное значение произведений элементов столбцов матрицы А; r – длина вектора , состоящего из минимальных элементов строк матрицы А ;

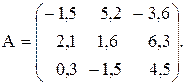
№2

Вычислить значение функции y= 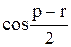, где p– среднее арифметическое элементов матрицы А , удовлетворяющих условию |a_ij| > 1; r– максимальный по модулю элемент вектор,состоящего из минимальных элементов строк матрицы А;

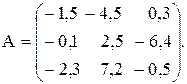
№3

Вычислить значение функции y= 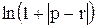, где p– среднее арифметическое отрицательных элементов матрицы А ; r – среднее геометрическое положительных элементов матрицы А ;

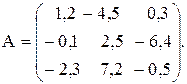
№4

Вычислить значение функции y= 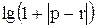, где p – длина вектора ,состоящего из максимальных элементов столбцов матрицы А; r –скалярное произведение этого вектора на тот же вектор , но упорядоченый по убыванию ;

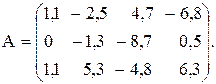
№5

Вычислить значение функции y= 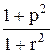, где p – максимальный элемент вектора y = А*В ;r – длина вектора y;

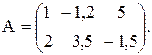
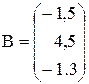
№6

Вычислить значение функции y= 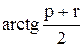, где p – среднее арифметическое элементов вектора В, удовлетворяющих условию 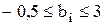; z– минимальный элемент матрицы А;

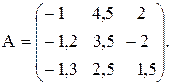
№7

Вычислить значение функции y= , где p – максимальный элемент матрицы С=А*В; r – среднее арифметическое положительных элементов матрицы С;

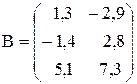
№8

Вычислить значение функции y= 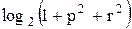, где p – среднее геометрическое элементов матрицы А , удовлетворяющих условию а_ij > 1;

r – минимальный помодулю элемент матрицы А;

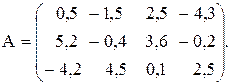
№9

Вычислить значение функции y= , где p – среднее геометрическое элементов матрицы А , удовлетворяющих условию 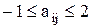; r– среднее арифметическое диагональных элементов матрицы А ;

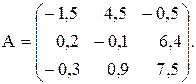
№10

Вычислить значение функции y= , где p – максимальное значение сумы элементов строк матрицы С=А*В; r – среднее геометрическое положительных элементов матрицы С;

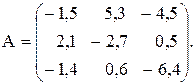
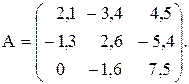
№11

Вычислить значение функции y= 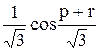, где p – среднее арифметическое положительных элементов матрицы А , лежащих ниже главной диагонали ; r – максимальный элемент среди элементов матрицы А, лежащих выше главной диагонали ;

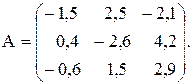
№12

Вычислить значение функции y= 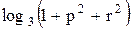, где p – максимальное значение произведений элементов столбцов матрицы А; r – длина вектора , состоящего из минимальных элементов строк матрицы А ;

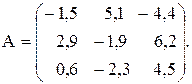
№13

Вычислить значение функции y= 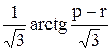, где p – длина вектора, состоящего из максимальных элементов столбцов матрицы А; r – среднее геометрическое модулей диагональных элементов матрицы А ;

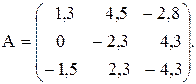
№14

Вычислить значение функции y= , где p – скалярнге произведение вектора ,состоящегоиз минимальных элементов строк матрицы А, на вектор , состоящий из максимальных элементов строк матрицы А; r – среднее арифметическое элементов матрицы А,удовлетворяющих условию | а_ij | < 1 или

| а_ij | > 2;

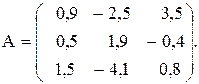
№15

Вычислить значение функции y= 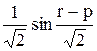, где p – максимальное значение произведений элементов столбцов матрицы А; r – длина вектора , состоящего из минимальных элементов строк матрицы А ;

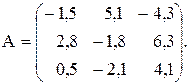
№16

Вычислить значение функции y= 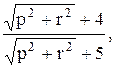где p – сума элементов матрицы А , удовлетворяющих условию ; r – максимальный элемент среди элементов матрицы А, удовлетворяющих условию | а_ij | < 2 ;

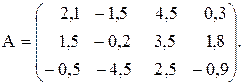
№17

Вычислить значение функции y= где p – минимальный элемент среди элементов матрицы А, удовлетворяющих условию –1< а_ij < 2;

r – длина вектора, состоящего из максимальных элементов столбцов матрицы А;

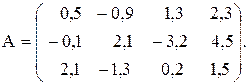
№18

Вычислить значение функции y= 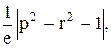где p –произвеление положительных элементов матрицы А, лежащих ниже главной диагонали;

r – минимальный элемент среди элементов матрицы А, удовлетворяющих условию | а_ij | < 0,5;

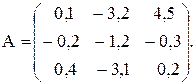
№19

Вычислить значение функции y= 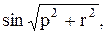где p – длина вектора ,состоящего из минимальных элементов строк матрицы А; r –скалярное произведение этого вектора на тот же вектор , но упорядоченый по возрастанию ;

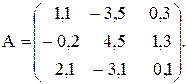
№20

Вычислить значение функции y= 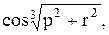где p– среднее арифметическое элементов матрицы А , удовлетворяющих условию a_ij < –1;

r– максимальный элемент среди диагональных элементов матрицы А;

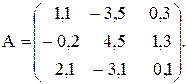
№21

Вычислить значение функции y= 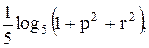где p – минимальный элемент среди элементов матрицы С=А*В, удовлетворяющих условию | С_ij | < 2;

r – среднее геометрическое модулей сумм элементов строк матрицы С;

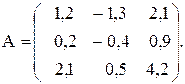
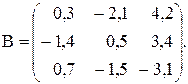
№22

Вычислить значение функции y= 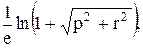где p – длина вектора

С=А*В; r – среднее арифметрическое положительных элементов вектора С;

.

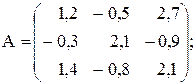
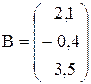№23

Вычислить значение функции y= где p – среднее геометрическое элементов матрицы А , удовлетворяющих условию a_ij > 3; r – длина вектора , состоящегоиз элементов матрицы А, лежащих на главной диагонали;

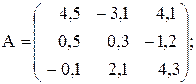
№24

Вычислить значение функции y= 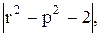где p – среднее арифметическое положительных произведений элементов столбцов матрицы А ;

r – длина вектора ,состоящего из сумм элементов строк матрицы А;

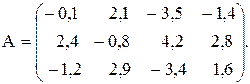
№25

Вычислить значение функции y= 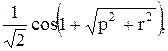где p – длина вектора ,составленного из произведений элементов строк матрицы А; r – минимальный элемент среди элементов матрицы А, удовлетворяющих условию 1< а_ij < 2;

№26

Вычислить значение функции y= 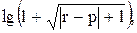где p – длина вектора, состоящего из минимальных элементов столбцов матрицы А; r – среднее геометрическое элементов матрицы А, удовлетворяющих условию a_ij > 4;

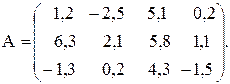
№27

Вычислить значение функции y= где p– максимальный по модулю элемент матрицы А; r – скалярное произведение вектора, составленного из минимальных элементов строк матрицы А, на тот же вектор , но упорядоченый по возростанию;

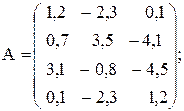
№28

Вычислить значение функции y= где p – среднее арифметическое произведений элементов строк матрицы А ;r – длина вектора ,состоящего из сумм элементов строк матрицы А;

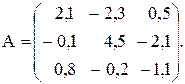
№29

Вычислить значение функции y= где p – среднее геометрическое модулей элементов матрицы А , удовлетворяющих условию

a_ij < 1; r – длина упорядоченного по убыванию вектора,состоящего из минимальных элементов столбцов матрицы А;

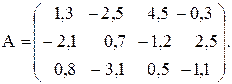
№30

Вычислить значение функции y= где p – максимальный элемент среди элементов матрицы А, удовлетворяющих условию | a_ij | < 1; r – среднее арифметическое элементов матрицы А, лежащих ниже главной диагонали;

Задание 13