ТЕМА 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ОСНОВЫ БИОАКУСТИКИ. УЛЬТРАЗВУК, ЕГО ПРИМЕНЕНИЕ В ФАРМАЦИИ

1. На рис. 1 представлены графики различных колебаний.

1.1. Гармонические колебания изображены на рисунках в, д, е, поскольку они осуществляются по закону синуса или косинуса, т.е. их графиком является синусоида или косинусоида, а в уравнении колебаний присутствует функция синус или косинус. Например, график в описывает незатухающие гармонические колебания, которые осуществляются с постоянной амплитудой, график д – затухающие гармонические колебания, амплитуда которых экспоненциально убывает во времени, график е – может соответствовать вынужденным гармоническим колебаниям, в ходе которых под действием гармонической вынуждающей силы сначала происходит нарастание амплитуды колебаний.

1.2. а) ; б)

Уравнение а описывает незатухающие гармонические колебания, уравнение б – затухающие гармонические колебания. В уравнениях:

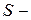смещение тела от положения равновесия в момент времени 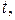смещение измеряется в единицах расстояния. В системе СИ в метрах.

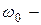циклическая частота свободных незатухающих колебаний, . Связана с линейной частотой , измеряемой в Герцах: . Показывает сколько радиан в единицу времени проходит колеблющееся тело.

- время, прошедшее от начала колебаний. Измеряется в единицах времени. В системе СИ в секундах; начальная фаза колебаний, , а фаза колебания в момент времени . Показывает положение колеблющегося тела в любой момент времени в единицах угла.

В уравнении б добавлен по сравнению с уравнением а множитель , где основание натурального логарифма, которое находится в отрицательной степени, что указывает на экспоненциальное снижение амплитуды гармонических затухающих колебаний, коэффициент затухания, показывающий во сколько раз уменьшается амплитуда колебаний в единицу времени [с^-1], что зависит от свойств среды и массы колеблющегося тела: 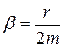,где коэффициент трения, 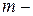масса колеблющегося тела; циклическая частота затухающих колебаний, по смыслу то же, что , но ус учётом действия коэффициента затухания:

2. На рис. 2 представлены вынужденные колебания, которые являются итогом взаимодействия собственных колебаний системы и колебаний системы под действием вынуждающей силы.

2.1. Собственным колебаниям системы соответствует кривая 2 на графике. Такие колебания могут возникать при однократном воздействии внешней силы, но их амплитуда убывает со временем вследствие действия силы трения. Как быстро они прекратятся, зависит от свойств среды и колеблющегося тела (уравнение б в предыдущем задании).

2.2.Действие вынуждающей силы отражает график 1. Видно, что она изменяется по гармоническому закону с постоянной амплитудой: , где 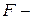значение силы в момент времени , 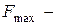амплитудное значение вынуждающей силы, циклическая частота вынуждающей силы.

2.3.Вынужденным колебаниям системы соответствует график 3.Сначала амплитуда этих колебаний постепенно возрастает (вследствие того, что колебания, возникающие под действием вынуждающей силы суммируются с собственными колебаниями системы. Эти два колебательных процесса имеют разную частоту, поэтому суммарное колебание меньше, чем то, которое могло бы быть, если бы не было собственных колебаний системы). Потом амплитуда устанавливается на постоянном уровне, поскольку свободные колебания затухают. В соответствии с этим выделяют: 1 период - установления вынужденных колебаний, 2 период – установившихся вынужденных колебаний.

3. На рис. 3 представлена зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы при различных коэффициентах затухания собственных колебаний системы.

3.1. Резонанс – это возрастание амплитуды вынужденных колебаний. Резонансная частота зависит от коэффициента затухания: при больших его значениях наступление резонанса невозможно ( ). Чем меньше , тем больше возрастает амплитуда. Т.е. для каждого тела существует набор резонансных частот, которые зависят от .

3.2.Резкое возрастание амплитуды вынужденных колебаний возникает при очень маленьких значениях (рис. 3). Это резкое возрастание часто подразумевают, когда говорят о резонансе. Оно возникает при малых , если частота вынуждающей силы равна частоте собственных колебаний системы. В таком случае свободные колебания не затухают, а суммируются с колебаниями под действием вынуждающей силы. Поскольку эти колебания имеют одинаковую частоту и фазу, возникает резкое увеличение амплитуды колебаний.

4. На рис. 4 представлены механические упругие волны двух видов.

4.1. Механическая волна – распространение механических колебаний в пространстве. Упругая волна – механическая волна, распространяющаяся в упругих средах за счёт сил упругих взаимодействий частиц среды.

Распространение механической волны в упругой среде представляет собой распространение энергии без переноса вещества: частицы среды колеблются около положения равновесия, передавая при взаимодействии энергии колебательного процесса.

4.2. На рис. 4 представлены два вида упругих механических волн: продольная (сверху) и поперечная (снизу). Продольная волна может возникать в жидкой, газообразной и твёрдой среде. При этом частицы, участвующие в волновом процессе, колеблются вдоль направления распространения волны.

Поперечная волна может возникать только в твёрдых телах. При этом частицы, участвующие в волновом процессе, колеблются перпендикулярно направлению распространения волны.

4.3.Фронт волны – геометрическое место точек, колеблющихся в одной фазе. По форме фронта волна может быть сферической, полусферической, плоской. Плоская волна – это волна, фронтом которой является плоскость.

Уравнение плоской волны (при ):

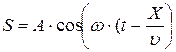
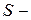смещение частицы среды, расположенной на расстоянии от источника волны, от положения равновесия в момент времени 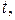прошедшее от начала колебания, циклическая частота колебаний частиц, , скорость волны.

5. На рис. 5 представлены графики акустических спектров различных звуков - тона, сложного тона, шума. Рассмотрите рисунок и ответьте на вопросы.

5.1.Спектр простого тона – в, т.к. в нём представлена одна линия, отражающая гармонические колебания одной частоты;

Спектр сложного тона - б, т.к. он представляет собой набор линий, отражающих набор гармонических колебаний различных частот, которые в сумме дают периодический, но не гармонический процесс. Основной тон имеет самую низкую частоту (первая линия), все остальные линии в спектре – обертоны;

Спектр шума – а, т.к. он сплошной. Шум негармонический и непериодический процесс. В нём невозможно выделить гармонические составляющие.

5.2. Спектр сложного тона – линейчатый: с помощью спектрального анализа сложное периодическое колебание разложено на гармонические колебания, амплитуда и частота которых представлена линиями. Спектр шума – сплошной, так как в нём составляющие не связаны между собой определёнными временными зависимостями.

6. На рис. 6 представлена область слышимости человека.

6.1. Между уровнем интенсивности звука (измеряется в Беллах) и его интенсивностью ( 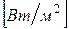существует логарифмическая зависимость: , где интенсивность звука, порог слышимости.

6.2. Порог слышимости – минимальная интенсивность звука, способная вызвать слуховое ощущение у человека. Для звука частотой 1000 Гц он составляет

Болевой порог – минимальная интенсивность звука, вызывающая болевое ощущение в органе слуха. Для звука частотой 1000 Гц он составляет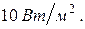

На рисунке кривая 3 соответствует порогу слышимости для звуков различных частот, кривая 1 – болевому порогу.

6.3. Чувствительность органа слуха к звукам различных частот неодинакова. Исходя из порога слышимости (кривая 3) видно, что его величина минимальна для звуков от 3000 до 5000 тысяч Герц (т.е. чувствительность к ним максимальна). Для звуков частотой менее 100 Гц и от 15000-20000 Гц – пороги слышимости существенно возрастают (кривая 3 резко уходит вверх справа и слева), т.е. чувствительность к этим звукам ниже.

7. Решите задачи:

7.1. Интенсивность звука в цехе составляла 10^-4 Вт/м². После проведения соответствующих работ она понизилась до 10^-6 Вт/м². Как изменился уровень интенсивности?

7.2. Уровень интенсивности звука работающего двигателя мотоцикла составляет 90 дБ. Каким был бы уровень интенсивности звука, если бы одновременно работали десять таких двигателей?

Найдём интенсивность звук двигателя: .

Интенсивность 10 двигателей: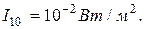

Уровень интенсивности 10 двигателей:

7.3. Автомобильный двигатель без глушителя издавал звук с уровнем интенсивности 100 дБ. Глушитель поставили на место, в результате чего интенсивность звука уменьшилась в 100 раз. Каким стал уровень интенсивности?

До установки глушителя интенсивность звука была равна: .

После установки глушителя: .

Уровень интенсивности после установки глушителя:

8. На рис. 7 представлены кривые равной громкости. По оси абсцисс обозначены частоты звуковых волн, по оси ординат – уровни их интенсивности, дБ. В центре рисунка над каждой кривой обозначена громкость в фонах, которой соответствует каждая кривая. Рассмотрите рисунок и ответьте на вопросы.

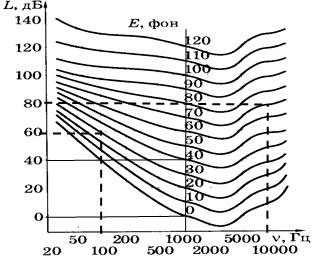8.1. Уровень интенсивности в децибелах и громкость в фонах совпадают для звуков частотой 1000 Гц.

Звук громкостью 30 фон частотой 100 Гц соответствует уровню интенсивности 60дБ.

Звук громкостью 70 фон частотой 10000 Гц соответствует уровню интенсивности 80дБ.

8.2. Громкость звука 1000Гц с уровнем интенсивности 40 дБ составляет 40 фон.

Для звука частотой 100 Гц с уровнем интенсивности 40 дБ громкость равна 0 фон.

Для звука частотой 5000 Гц с уровнем интенсивности 40 дБ громкость равна 40 фон.

Звуки 1000Гц и 5000Гц с уровнем интенсивности 40 дБ человек слышит одинаково громко, а звук 100Гц такого же уровня интенсивности человек не слышит.

8.3. Этот звук имел частоту 200 Гц (пересечение перпендикуляров к 40 дБ на оси ординат с кривой 30 фон. От точки пересечения – перпендикуляр на ось абсцисс)

9. На рис. 8 представлены особенности распространения ультразвука.

9.1. Ультразвук – это звук(продольная упругая механическая волна) частотой выше 20 000 Гц. Получают: 1.с помощью обратного пьезоэлектрического эффекта. Пьезокристалл удлиняется и укорачивается (колеблется) вдоль пьезоэлектрической оси под действием переменного электрического поля: ( напряжённость электрического поля, максимальная напряжённость, циклическая частота колебаний, время). 2. магнитострикционным методом. Стержень из ферромагнетика увеличивается и уменьшается в объёме (колеблется) под действием переменного магнитного поля: ( напряжённость электрического поля, максимальная напряжённость, циклическая частота колебаний, время).

9.2. Отражение ультразвука наступает при его попадании на границу двух сред, различающихся акустическим сопротивлением (импедансом). Степень отражения ультразвука зависит от соотношения акустических сопротивлений этих двух сред.

Коэффициент отражения ультразвуковых волн можно рассчитать по формуле: где 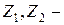акустические импедансы сред.

, где плотность среды, а скорость распространения в среде ультразвука.

На рисунке б степень отражения будет больше, т.к. большая разница между акустическими сопротивлениями сред.

9.3. Отражение ультразвука используется в ультразвуковой диагностике. Информацию о состоянии внутренних органов получают на основе эхосигналов – отраженных внутренними органами ультразвуковых волн. Комплекс методов ультразвуковой диагностики поэтому называется эхографией.

10.При прохождении ультразвука через вещество его интенсивность уменьшается (рис.9).

10.1. Интенсивность ультразвука при прохождении через вещество уменьшается по экспоненциальному закону: , где интенсивность после прохождения, начальная интенсивность, коэффициент ослабления, толщина поглощающего вещества.

10.2. Интенсивность ультразвука при прохождении через вещество изменяется вследствие его поглощения и рассеивания.

10.3. Существует три основных первичных механизма действия ультразвуковой энергии на вещество при её поглощении: 1 механическое действие (колебания микрочастиц вещества, в жидкости – разрывы целостности), 2. тепловое (нагревание вещества вследствие усиления движения в нём микрочастиц), 3. физико-химическоедействие (инициация и ускорение физических процессов и химических реакций). В фармации эти явления применяются для изготовления лекарственных препаратов: на пример, изготовление порошков, суспензий, липосом и .т.д.

10.4.На рисунке изображено явление кавитации – образование в жидкости пузырьков, заполненных воздухом, вследствие разрыва целостности воды под действием ультразвука. Кавитационные пузырьки – энергетические невыгодное состояние жидкости. Поэтому они «схлопываются», а избыток свободной энергии выделяется в жидкость, производя интенсивное механическое и тепловое действие. В результате – ультразвук оказывает разрушающее действие на структуры. Поэтому кавитация применяется в изготовлении лекарств: например, получение соков из растительного сырья, диспергирование различных препаратов и т.д., а также в стерилизации медицинского инструментария (рис.б).