ТЕМА 3. ОСНОВЫ БИОЛОГИЧЕСКОЙ ТЕРМОДИНАМИКИ, БИОМЕМБРАНОЛОГИИ, ЭЛЕКТРОКАРДИОГРАФИИ.

1.На рис. 1 схематически изображены термодинамические системы.

1.1.Термодинамическая система – это тело или система тел, отделённая мысленными или реальными границами от окружающей среды.

Первая на рис.1 система – изолированная – не обменивается с окружающей средой ни веществом, ни энергией. Таких систем в реальности не существует, но на протяжение короткого промежутка времени можно изолированной считать достаточно теплоизолированную систему.

Вторая на рис.1 система – закрытая – обменивается с окружающей средой энергией, но не веществом. Например, термос с чаем.

Третья система – открытая – обменивается энергией и веществом с окружающей средой (клетка, организм в целом).

1.2. Равновесное состояние изолированной системы и стационарное состояние открытой системы имеют сходство в том, что это устойчивые состояния: их параметры не меняются во времени. Но в равновесном состоянии параметры состояния одинаковы в любой точке системы, не существует градиентов, энтропия системы максимальна, а термодинамические потенциалы равны нулю. В стационарном состоянии параметры состояния могут различаться в разных частях системы, существуют градиенты, вследствие чего могут протекать различные процессы переноса, изменение энтропии во времени минимально (т.е. она поддерживается на определённом, но не максимальном уровне), существуют и поддерживаются термодинамические потенциалы.

2.Охарактеризуйте 1 и 2 законы (начала) термодинамики:

2.1.1 начало термодинамики представляет собой закон сохранения энергии. Для изолированной системы: полная энергия системы есть величина постоянная. Другая формулировка – невозможно создать вечный двигатель 1 рода, который бы производил работу без поступления энергии извне.

Уравнение 1 начала термодинамики имеет вид: ,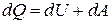

где 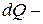теплота – энергия, которая передаётся системе или отдаётся системой в процессе всех видов теплопередачи (теплопроводностью, конвекцией, тепловым излучением), измеряется в Джоулях.

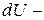внутренняя энергия системы – суммарная потенциальная и кинетическая энергия всех частиц, составляющих систему, измеряется в Джоулях.

работа – энергия, передаваемая системе или отдаваемая ею, в процессе силовых взаимодействий с окружающими телами, измеряется в Джоулях.

Все величины измеряются в Джоулях, поскольку представляют собой разные формы энергии.

2.2. Живые организмы в процессе жизнедеятельности используют теплоту, заключённую в химических связях различных веществ. Сначала происходит расщепление белков, жиров и углеводов пищи до мономеров, которые всасываются в кровь, поступают в клетки, окисляются, а выделяющаяся при этом энергия аккумулируется в макроэргических связях АТФ (и других макроэргов). Энергию гидролиза АТФ живые организмы используют на поддержании внутренней энергии и совершение всех видов биологической работы (химической – синтез новых веществ, электрической – поддержание мембранного потенциала, механической – дыхание и кровообращение и т.д.)

2.3.Q₁ = (Q₂+Q₃) = (Q₄+Q₅+Q₆). Это соотношение описывает принцип Гесса, который гласит: тепловой эффект химической реакции не зависит от пути перехода исходных веществ в продукты реакции, а определяется только энтальпиями (теплосодержанием) исходных веществ и продуктов реакции. Этот принцип можно считать следствием закона сохранения энергии.

2.4. Невозможно создать вечный двигатель 2 рода, который бы всю подводимую к нему теплоту превращал бы в работу. Невозможен самопроизвольный переход теплоты от менее нагретого тела к более нагретому телу. Закон указывает на направление самопроизвольного протекания процессов. Следствие из закона – часть любой формы энергии всегда рассеивается в виде теплоты, в связи с чем процессы в реальных термодинамических системах всегда необратимы.

2.5. Критериями самопроизвольного протекания процессов могут служить: 1. изменение энтропии. Энтропия ( ) – это функция состояния ТДС, изменение которой в ходе процесса равно количеству приведённой теплоты: 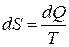, где 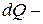изменение теплоты в ходе процесса, 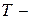термодинамическая температура, при которой проходит процесс. Энтропия является количественной мерой рассеяния энергии в теплоту. Любой самопроизвольный процесс всегда сопровождается увеличением энтропии, т.е. .

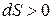2 критерий самопроизвольного протекания процесса – это уменьшение термодинамических потенциалов системы (в зависимости от системы и процесса это могут быть электрохимический потенциал, потенциал Гиббса, свободная энергия Гельмгольца, энтальпия и т.д.)

2.6. Энтропию как функцию термодинамической вероятности состояния системы характеризует уравнение Больцмана: 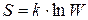. Термодинамическая вероятность – это число микросостояний системы, посредством которого может быть реализовано данное макросостояние системы. Она всегда больше 1. Чем больше 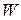, тем более вероятно данное состояние системы. ТДС всегда стремиться в наиболее вероятное состояние, т.е. к увеличению 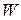. При этом будет, согласно уравнению Больцмана, и энтропия. Поэтому в ходе самопроизвольных процессов энтропия будет возрастать.

2.7. 2.7.1. Данный метод называется прямой биокалориметрией. При его проведении измеряется количество теплоты, выделенное живым организмом, в изолированной камере. Все процессы, которые происходят в организме, протекают с рассеянием части энергии в виде теплоты. Если организм не совершает внешней работы, то в конечном итоге вся используемая в данный промежуток времени энергия в процессе жизнедеятельности превращается в теплоту. Здесь проявляется действие второго начала термодинамики. Измеряя эту теплоту, можно судить об интенсивности основного обмена у живых организмов, и составлять рацион питания, учитывая первый закон термодинамики.

2.7.2. Температура тела – это мера теплового движения частиц системы, характеризующая их суммарную кинетическую энергию. Чем больше выделяется в процессе жизнедеятельности теплоты, тем больше будет температура. Измерение температуры в таком случае будет отражать интенсивность процессов метаболизма (например, при воспалении температура увеличивается). Методы измерения температуры тела называются термометрией.

2.7.3.Количество теплоты, расходуемой организмом, определяют с помощью методов прямой и непрямой калориметрии (определяют уровень основного обмена) и специальных таблиц, которые с учётом вида трудовой деятельности человека позволяют определить количество необходимой для этого энергии. Количество поступающей энергии определяют по калорийности продуктов питания, употребляемых человеком. Эту энергию можно измерить непосредственно, сжигая продукты в калориметрической бомбе, или с помощью специальных таблиц, в которых указана калорийность пищевых продуктов. Сопоставление поступающей энергии и расходуемой энергии должно соответствовать 1 началу термодинамики – закону сохранения энергии.

2.7.4. Эргометрия – измерение количества энергии, необходимой для выполнения той или иной трудовой деятельности человека.Это количество энергии должно прибавляться к измеренному с помощью биокалориметрии уровню основного обмена (энергии необходимой для поддержания процессов жизнедеятельности в покое) при составлении пищевого рациона. Мы используем 1 закон термодинамики – для осуществления всех процессов необходима энергия.

3.Запишите уравнение и теорему Пригожина. Поясните их смысл. Уравнение Пригожина показывает, из каких компонентов состоит приращение энтропии 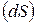в открытой системе (в т.ч. в теле человека): 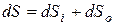, где приращение энтропии внутри системы, изменение энтропии вследствие обмена энтропий с окружающей средой. В уравнение также вводят фактор времени и говорят о производстве энтропии и получают: 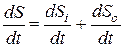, т.е. скорость изменения энтропии равна сумме скорости прироста энтропии внутри системы вследствие необратимости процессов и скорости обмена энтропией с окружающей средой.

В стационарном состоянии , , а 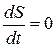. Последняя формула отражает теорему Пригожина – в стационарном состоянии скорость приращения энтропии открытой системы минимальна.

4.На рис. 4а показано химическое строение глицерофосфолипида.

4.1.1- остаток трёхатомного спирта глицерола

2- остатки насыщенных или ненасыщенных жирных кислот

3. – остаток фосфорной кислоты

4 – аминоспирт

5 (1+3+4) – «головка» фосолипида, 2 –«хвостики».

4.2. «Головка» обладает сродством к воде, она гидрофильна; «хвостики» отталкиваются от воды – они гидрофобны. Молекулы, имеющие гидрофильную и гидрофобную части, называются амфифильными.

4.3. Амфифильность молекул фосфолипидов способствует формированию структуры мембраны в виде бислоя за счёт гидрофобных взаимодействий. На рис. 4б представлены мицеллы - структуры, которые формируются путём самосборки при добавлении фосфолипидов в воду с последующим интенсивным встряхиванием жидкости. За счёт гидрофобных взаимодействий гидрофобные хвостики фосфолипидов «прячутся» от воды, с которой контактируют гидрофильные головки. При этом образуется замкнутая – сферическая структура.

4.4.Липосомы - бислойные замкнутые сферические структуры, которые образуются путём самосборки при добавлении липидов в полярный растворитель и перемешивании полученного раствора, например, ультразвуком. Также их можно получить воздействуя на природные мембраны, погружённые в жидкость, ультразвуком. Липосомы можно применять как модели биологических мембран и, погружая в раствор различных веществ, изучать проницаемость для них мембран; добавляя различные вещества в липосомы, можно смоделировать мембранымитохондрий, эндоплазматического ретикулума и изучать их свойства; вводя внутрь липосом лекарственные препараты, можно доставлять их внутрь тела без повреждения ферментами желудка; в косметологии – в крема включают липосомы с биологически активными веществами и т.д.

5.На рис. 5 схематично представлены различные уровни организации белковой молекулы. Рассмотрите схемы и ответьте на вопросы:

5.1.На рис.5 представлены: 1. первичная структура белковой молекулы – цепочка аминокислот, соединённых между собой пептидной (ковалентной) связью; 2. вторичная структура – спираль, сформированная с помощью водородных связей на основе первичной структуры, либо складчатая структура, сформированная чаще всего из нескольких полипептидных цепей с помощью водородных связей. 3. третичная структура – глобула, фиксированная всеми видами слабых взаимодействий – водородными и ионными связями, ван-дер-ваальсовыми и гидрофобными взаимодействиями (при ведущей роли последних). Если в первичной структуре представлены серосодержащие аминокислоты, то в третичной структуре могут образовываться дисульфидные мостики.

5.2. Также возможно формирование четвертичной структуры – надструткуры, образованной несколькими глобулами Формируется за счёт гидрофобных взаимодействий.

6.Рассмотрите рис. 6, на котором изображено строение мембраны.

6.1. Липиды, белки, углеводы в комплексе с белками (гликопротеины и протеогликаны) или липидами (гликолипиды).

6.2. Молекулы липидов амфифильны: они имеют гидрофильные головки и гидрофобные хвостики. Расположение их в виде бислоя способствует тому, что гидрофобные хвостики не контактируют с жидкими средами, а гидрофильные головки с одной стороны мембраны контактируют с цитоплазмой клетки, с другой – с межклеточной жидкостью.

6.3. Ведущая роль принадлежит гидрофобным взаимодействиям, которые состоят в отталкивании гидрофобными частицами молекул воды и сближении этих частиц между собой. При этом происходит увеличение энтропии системы, но никаких химических связей не образуется. Поэтому говорят, что гидрофобные взаимодействия имеют термодинамические причины, а точнее – энтропийную природу.

6.4.Белки в мембране могут быть интегральными (в той или иной степени пронизывают мембрану, часто насквозь) и периферическими (находятся на поверхности). Интегральные белки более прочно связаны с мембраной, поскольку фиксированы в ней гидрофобными взаимодействиями (их молекулы, как и молекулы липидов амфифильны). Периферические белки связаны с мембраной слабыми связями, преимущественно ионными, в связи с чем менее прочно с ней связаны, чем интегральные белки.

6.5. Молекула белка должна быть амфифильной: её гидрофобная часть контактирует с гидрофобными хвостиками, а гидрофильная – с гидрофильными головками, межклеточной жидкостью и цитоплазмой.

6.6.Мембрана является жидкостью: при обычной температуре её консистенция соответствует консистенции оливкового масла. Молекулы мембраны подвижны, как в любой жидкости. Однако они расположены в мембране строго упорядоченным образом: липиды параллельно длинными осями друг другу и перпендикулярно поверхности мембраны, а белки поддерживаются липидами в необходимой для функционирования конформации. Упорядоченность – свойство кристалла. Поэтому мембрану называют «жидким кристаллом». Для таких веществ характерны фазовые переходы (из золь в гель, и наоборот) в зависимости от температуры и их химического состава.

7.На рис. 7 показано влияние химического состава липидов на биофизические свойства мембраны.

7.1. Различие между насыщенными и ненасыщенными кислотами состоит в наличии двойных связей в цепочечных молекулах ненасыщенных кислот. В них около двойных связей образуются изгибы цепи, т.е. возможны изменения конфигурации.

7.2.Если в мембране представлены липиды с насыщенными хвостиками, то они расположены в монослое плотно друг к другу, а бислой имеет относительно большую толщину (вследствие отсутствия изгибов в молекулах насыщенных жирных кислот). Если в мембране представлены липиды с ненасыщенными хвостиками, то они расположены в монослое более рыхло, а бислой имеет меньшую толщину (вследствие наличия изгибов в молекулах насыщенных жирных кислот). В таком случае (при наличии ненасыщенных хвостиков) мембрана более текучая и более проницаема для различных веществ.

7.3. Холестерин может увеличивать плотность мембран, встраиваясь между молекулами фосфолипидов, и, наоборот, увеличивать текучесть мембраны, уменьшая гомогенность химического состава фосфолипидов.

7.4. Лиотропным полиморфизмом.

8. На рис. 8 схематично показано влияние изменений температуры на состояние молекул фосфолипидов в мембране и её биофизические свойства (текучесть, проницаемость). Объясните рисунок. Как называется зависимость биофизических свойств мембраны от температуры? При низких температурах хвостики липидов полностью вытянуты, липиды плотно прилегают друг к другу, их движения ограничены, а толщина мембраны максимальная. В таком состоянии (гель) текучесть мембраны и проницаемость её для различных веществ относительно небольшая. При повышении температуры выше критического уровня – мембрана переходит в золь-состояние. Благодаря увеличению температуры увеличивается подвижность липидов и их хвостиков, образуются изгибы хвостиков, липиды за счёт этого неплотно прилегают друг к другу, а толщина билипидного слоя уменьшается. Всё это способствует увеличению текучести мембраны и её проницаемости для различных веществ. Зависимость состояния мембраны от температуры называется термотропным полиморфизмом.

9. Рассмотрите рис. 9, на котором схематично показаны различные виды транспорта веществ через мембрану, и ответьте на вопросы:

9.1.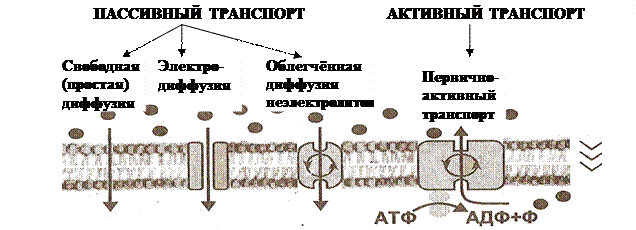

9.2. Простая диффузия осуществляется непосредственно через бислой липидов, электродиффузия – через ионные каналы, облегчённая диффузия – с помощью молекул-переносчиков. На схеме показано наличие каналов и переносчиков.

9.3. Непосредственно через бислой липидов могут проникать мелкие молекулы (углекислый газ, кислород, угарный газ и т.д.) и липофильные, т.е. липидорастворимые, вещества (спирт, эфир, стероидные гормоны и т.д.)

10. Рассмотрите рис. 10, на котором представлены графики зависимости плотности потока вещества через мембрану от концентрации транспортируемых молекул при свободной и облегчённой диффузии.

10.1. Сходство свободной и облегчённой диффузии в том, что это виды пассивного транспорта веществ через мембрану, т.е. они осуществляются без затраты энергии метаболизма по градиенту концентрации вещества. Однако при свободной диффузии вещества проникают в клетку (или из неё) непосредственно через бислой липидов или поры, а при облегчённой – с помощью белков-переносчиков.

10.2. Для облегчённой диффузии характерны: 1. высокая степень специфичности переноса (белок-транспортёр связывает только определённое вещество, в некоторых случаях различая даже стерео-изомеры вещества), 2. высокая скорость переноса (на график – крутой подъём кривой), 3. феномен насыщения: скорость переноса достигает максимального уровня и несмотря на увеличение градиента конценрации остаётся на постоянном уровне (связано с конечным числом переносчиков в мембране), 4. возможность ингибирования транспорта (например, фармпрепаратами, конкурентно или неконкуренто блокирующими белок-переносчик).

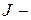10.3. Уравнение Фика описывает свободную диффузию: в общем виде - , где плотность потока вещества, коэффициент диффузии, 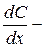градиент конценрации (плотность потока вещества, или скорость диффузии, пропорциональна градиенту концентрации); для биомебран: 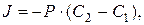где 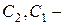концентрации вещества внутри и снаружи клетки, 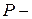проницаемость мембраны для вещества ( 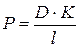, где 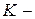коэффициент распределения вещества между мембраной и цитоплпзмой и межклеточной жидкостью, который зависит от растворимости вещества в липидах, 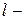толщина мембраны).

10.4.Примерами облегчённой диффузии неэлектролитов служат поступление глюкозы в эритроциты, мышечные клетки. Наличие, белков –переносчиков глюкозы в их мембранах может отражать приспособление к выполняемой ими функции. В обоих случаях глюкоза служит для получения клеткой энергии.

11.Рассмотрите рис. 11, на котором схематично показано строение ионного канала мембраны, управляемого электрическим полем.

11.1. 1. – мембрана; 2. потенциалчувствительныйэлемент служит для открытия и закрытия ворот канала в зависимости от величины мембранного потенциала; 3. ворота канала – служат для регуляции поступления ионов через канал, 4. пора канала – заполнена водой, через неё происходит ток ионов, 5. «селективный фильтр» - самая узкая часть канала, которая не пропускает ионы, большие по размеру, чем ион, для которого предназначен данный канал; 6. элементы цитоскелета – опорная функция, удерживают белок канала в нужной конформации, 7. остатки углеводов – указывают наружную часть мембраны, роль в транспорте ионов неясна.

11.2. Через ионные каналы осуществляется электродиффузия – транспорт ионов. Для транспорта ионов необходимы каналы, так как билипидный слой непроницаем для них (большой потенциальный барьер).

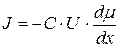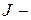11.3. Данный вид транспорта описывается уравнением Теорелла: , где плотность потока ионов, 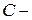концентрация ионов в растворе, 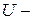подвижность ионов в растворе, градиент электрохимического потенциала ионов. Формулировка: плотность потока ионов через мембрану пропорциональна движущей силе электродиффузии – градиенту электрохимического потенциала иона.

В уравнении Нернста-Планка, которое также описывает электродиффузию, градиент электрохимического потенциала представлен в виде его составляющих – градиента электрического потенциала 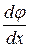и градиента концентрации -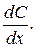

12.На схеме, представленной на рис. 12 показано функционирование одного из видов транспорта в мембране. Рассмотрите рисунок и ответьте на вопросы.

12.1. На рис. 12 представлен один из видов активного транспорта - натрий-калиевый насос плазматической мембраны. За один цикл он транспортирует 3 иона натрия из клетки, и 2 иона калия в клетку против градиентов их электрохимических потенциалов. Белок насоса имеет название – натрий-калий–магний-зависимая АТФаза, что указывает на то, что белок катализирует реакцию гидролиза АТФ.

12.2. Это активный вид транспорта, так как ионы движутся против градиентов их электрохимических потенциалов с использованием энергии гидролиза АТФ. За счёт энергии гидролиза АТФ происходит реакция фосфорилирования белка насоса, к активному центру которого присоединяются 3 иона натрия. В результате этой реакции белок изменяет конформацию так, что ионы натрия оказываются снаружи клетки. Там они освобождаются из активного центра за счёт того, что ионы калия имеют к нему большее сродство. Это приводит к реакции дефосфорилирования белка насоса, он меняет свою конформацию на прежнюю и ионы калия оказываются внутри клетки.

12.3.Существуют кальциевые насосы мембран эндоплазматического ретикулума, водородная помпа, йодный насос.

12.4.Активный транспорт ионов калия и натрия осуществляться не будет. Некоторое время, до исчезновения градиента, будет происходить пассивный транспорт калия через каналы, но он тоже быстро прекратиться, так как градиент создаётся активным транспортом.

13.На рис. 13 схематично показаны виды вторично-активного транспорта через плазматическую мембрану клетки.

13.1. Глюкоза в энтероциты кишечника поступает путём вторично-активного транспорта, который осуществляется против градиента концентрации, но не за счёт энергии гидролиза АТФ, а за счёт энергии натриевого градиента, накопленного в ходе первично-активного транспорта. Это симпорт – ионы натрия и глюкоза движутся в одном направлении – в клетку.

13.2. Натрий – кальциевый обменник – один из видов вторично-активного транспорта. Это антипортная транспортная система: натрий движется по своему градиенту в клетку, а кальций – против своего градиента из клетки. Существует в кардиомиоцитах и других мышечных клетках, способствуя удалению из цитоплазмы кальция. ,то необходимо для мышечного расслабления.

14. На рис. 14 представлена схема регистрации мембранного потенциала клетки с помощью микроэлектродов.

14.1. Мембранный потенциал – разность потенциалов между внутренней и наружной поверхностями мембраны клетки. В данном случае зарегистрировали потенциал -100мВ.

14.2.1. неравномерное распределение ионов внутри и снаружи клетки: внутри много калия и органических анионов, мало натрия и хлора, снаружи – много натрия и хлора, мало калия. Т.е. для ионов существуют градиенты. 2. неодинаковая проницаемость мембраны для различных ионов – в покое мембрана проницаема только для ионов калия. 3. электрогенность натрий- калиевого насоса (на 3 положительных иона натрия, выкачанных из клетки, насос закачивает лишь 2 иона калия).

14.3.Мембранный потенциал покоя имеет отрицательное значение, так как ионы калия, для которых в покое мембрана проницаема, по своему градиенту выходят наружу (+ электрогенность натрий-калиевого насоса). Поэтому внутри клетки потенциал отрицателен по отношению к наружному потенциалу.

Уравнение Нернста позволяет рассчитать потенциал электрохимического равновесия иона – разность потенциалов на мембране, которая бы остановила диффузию этого иона по градиенту концентрации при условии, что мембрана проницаема только для одного вида ионов. Уравнение Нернста в общем виде имеет вид: 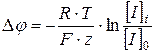, где потенциал электрохимического равновесия иона, 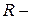универсальная газовая постоянная, 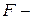число Фарадея, 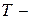термодинамическая температура, заряд иона, соответственно внутренняя и наружная концентрация иона. Если в уравнение подставить концентрации калия, то получиться величина потенциала электрохимического равновесия ионов калия - 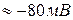, что соответствует измеренной с помощью микроэлектродной техники величине МПП ( ).

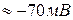14.4. Потому что мембрана проницаема частично и для других ионов – для ионов натрия и хлора. Более точно МПП можно вычислить с помощью уравнения Гольдмана-Ходжкина:

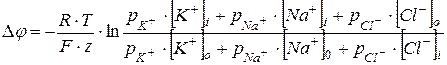. Обозначения те же, что в уравнении Нернста, только добавляются проницаемости мембраны для ионов. В покое .

15. В эксперименте на гигантском аксоне кальмара цитоплазму заменяли искусственным солевым раствором, содержащим различную концентрацию ионов калия. При этом измеряли величину мембранного потенциала покоя. На рис. 15 график отражает результаты опыта. Проанализируйте график. Сделайте вывод о том, как и почему изменение концентрации ионов калия приводит к сдвигу величины мембранного потенциала.

На графике видно, что приращение внутренней концентрации ионов калия от 0 до величины, которая наблюдается в естественных условиях, приводит к увеличению мембранного потенциала до уровня МПП. Это свидетельствует о том, что именно диффузия ионов калия по градиенту своего электрохимического потенциала изнутри клетки наружу обуславливает величину и отрицательное значение МПП.

16.На рис. 16 представлены графики потенциала действия различных возбудимых тканей. Рассмотрите рисунок и ответьте на вопросы.

16.1.Потенциал действия – быстрое колебание величины мембранного потенциала. Фазы: 1. деполяризация – изменение МП в положительную сторону; 2. реполяризация – возврат МП к уровню МП покоя, овершут – точка «перегиба».

16.2. Неодинаковы, поскольку у них различные ионные механизмы.

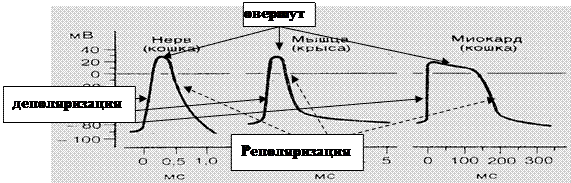16.3. В нерве с помощью ПД передаётся информация, в мышце ПД необходим для выхода кальция из потенциалзависимых кальциевых каналов эндоплазматического ретикулума, что способствует инициации мышечного сокращения.

17.На рис. 17 пунктирной линией обозначен ПД нервного волокна (кривая I). Сплошными линиями изображены изменения проводимости мембраны для потенциалобразующих ионов (кривые II и III).

17.1. Кривая ІI- для ионов натрия, кривая ІІІ – для ионов калия.

17.2. а). Деполяризация обусловлена поступлением ионов натрия в клетку из-за резкого увеличения проницаемости мембраны для этих ионов, б).Реполяризация обусловлена инактивацией натриевых каналов и увеличением проницаемости мембраны для ионов калия,

17.3. Уравнение Нернста для ионов натрия имеет вид: , где потенциал электрохимического равновесия иона, 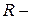универсальная газовая постоянная, 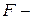число Фарадея, 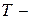термодинамическая температура, заряд иона, соответственно внутренняя и наружная концентрация иона. Если в уравнение подставить концентрации натрия, то получиться величина потенциала электрохимического равновесия ионов калия - 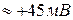, что соответствует измеренной с помощью микроэлектродной техники величине МП на овершуте потенциала действия ( ). Измеренный с помощью микроэлектродов потенциал немного меньше вследствие диффузии ионов калия изнутри клетки наружу, которая также постепенно увеличивается при деполяризации мембраны.

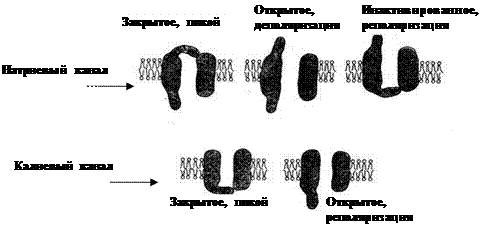18.На рис. 18 представлено состояние натриевых и калиевых каналов во время различных фаз потенциала действия.

18.1.

18.2. У калиевых каналов только активационные ворота, а у натриевых – активационные и инактивационные. Поэтому калиевые каналы могут быть только открыты или закрыты, а натриевые – ещё инактивированы.

18.3. В нервном волокне представлены потенциалзависимые каналы – их состояние зависит от уровня мембранного потенциала.

19. Гигантское нервное волокно поместили в изотонический солевой раствор ионов натрия. В ответ на электрическое раздражение в нем возник потенциал действия (рис.2 а). После этого ¼ часть ионов калия, находящихся внутри волокна заменили ионами натрия и вновь записали потенциал действия (рис.2б). Затем заменили внутри волокна ½ часть ионов калия ионами натрия, записав потенциал действия.

19.1.Амплитуда ПД в условиях опыта уменьшалась, а продолжительность ПД – увеличивалась.

19.2. Амплитуда ПД уменьшалась, поскольку уменьшался градиент концентрации ионов натрия (поступление натрия в клетку – причина деполяризации мембраны), длительность ПД увеличивалась, т.к. уменьшался градиент концентрации ионов калия (выход калия из клетки – причина реполяризации мембраны во время ПД).

20.Нерв рака, содержащий два нервных волокна, раздражали нервными импульсами. Возникающие при этом потенциалы действия регистрировали (рис. 20). Вначале нерв был погружён в физиологический раствор (кривая а). Затем его перенесли в раствор, из которого были исключены ионы натрия и заменены ионами холина, не проникающими через мембрану. Записи «б» - «е» сделаны через равные промежутки времени после замены натрия холином.

20.1.Амплитуда потенциала действия уменьшалась по мере того, как уменьшалось количество натрия в растворе, а когда градиент натрия исчез – исчезли ПД при электрическом раздражении нерва.

20.2. Амплитуда ПД уменьшалась, поскольку уменьшался градиент концентрации ионов натрия (поступление натрия в клетку – причина деполяризации мембраны).

21.На рис. 21 изображено проведение нервного импульса по двум типам волокон.

21.1. 1. Закон бездекрементного распространения ПД по нервному волокну, обладающему физиологической и анатомической целостностью. (ПД возникает по закону «всё или ничего»: если деполяризация мембраны достигает критического значения, то он возникает в каждом последующем участке нервного волокна с одинаковой амплитудой. Для проведения ПД необходима анатомическая целостность волокна и физиологическая, т.е. натриевые каналы не должны быть инактивированы).

2. Закон независимого распространения ПД по нервным волокнам в составе нерва (ПД не распространяется на соседние нервные волокна благодаря шунтирующему влиянию межклеточной жидкости и миелиновой оболочке).

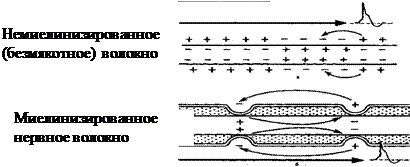3. Закон двустороннего, но не обратного распространения ПД по нервному волокну (от места возникновения ПД может распространяться в обе стороны, т.к. свойства нервного волокна одинаковы во всех его точках. Однако обратно ПД не распространяется вследствие инактивации на какое-то время натриевых каналов – состояние рефрактерности).

21.2.

Миелинизированное нервное волокно покрыто миелином, который представляет собой оболочку шванновских клеток. Существуют участки не покрытые миелином – перехваты Ранвье, в которых повышено количество натриевых каналов, отвечающих за генерацию ПД. Немиелинизированные волокна не покрыты миелином, расположение в них натриевых каналов равномерное.

21.3. Распространение ПД в обоих типах волокон происходит за счёт локальных электрических токов, возникающих в соседних с возбуждённым участках волокна. Эти токи внутри волокна направлены от возбуждённого участка к невозбуждённому, а снаружи – от невозбуждённого к возбуждённому. В результате в соседних участках нервного волокна возникает деполяризация, которая, достигая критического уровня, приводит к возникновению нового ПД. В немиелинизированном волокне ПД возникает от точки к точке. В миелинизированном волокне локальные токи возникают между перехватами Ранвье, в результате ПД распространяется сальтоторно, т.е. минуя участки, покрытые миелином. Поэтому ПД быстрее распространяется по миелинизированным волокнам.

22.На рис. 22 схематично мембрана кардиомиоцита в состоянии покоя (а) и в период охвата его возбуждением (б).

22.1. При возбуждении мембраны его мембрана снаружи становится электроотрицательной по отношению к внутренней среде, на рис. 5б – это правая часть клетки.

22.2.Для описания электрического поля кардиомиоцита на рис. 5б можно применить модель электрического диполя. Э.диполь – это два заряда, одинаковые по величине, но противоположные по знаку, расположенные на малом расстоянии друг от друга, называемом плечом диполя. Главная характеристика диполя – дипольный момент 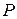– вектор, численно равный произведению заряда 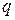на плечо диполя 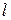, и направленный от отрицательного заряда к положительному: 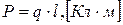. Потенциал поля диполя 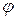определяется свойствами среды, в которой образуется поле, - ( 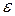), величиной дипольного момента 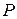, расстоянием от диполя до точки, в которой определяется потенциал, - 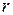, направления вектора дипольного момента относительно вектора соединяющего точку поя с диполем ( ): .

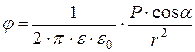22.3. Возможно состояние, когда вся поверхность кардиомиоцита электроотрицательна, т.е. клетка полностью возбуждена. В этом случае, и в случае, представленном на рис 22а, кардиомиоцит не обладает дипольным моментом. В случае на рис. 22б (при постепенной деполяризации и реполяризации мембраны), когда часть поверхности электроотрицательна, а часть электроположительна, кардиомиоцит представляет собой диполь, обладающий дипольным моментом.

23. На рис. 23 показаны записанные одновременно потенциал действия клетки желудочка сердца (сверху) и электрокардиограмма (снизу).

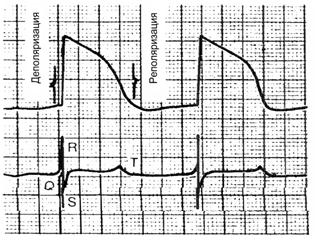23.1.

23.2.Комплекс соответствует деполяризации, зубец Т – реполяризации кардиомиоцитов желудочков сердца.

24. На рис. 24 представлена схема трёх стандартных отведений электрокардиограммы Эйнтховена.

24.1. Равносторонний треугольник.

24.2. Не изменится: конечности считают проводниками электрического тока.

24.3.Для устранения наводок – помех в записи, искажающих форму ЭКГ.

25.На рис. 25 представлена нормальная ЭКГ, записанная в одном из стандартных отведений Эйнтховена.

25.1.Зубцы 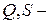отрицательные, положительные.

25.2.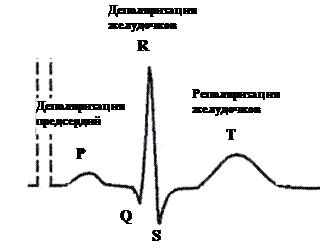

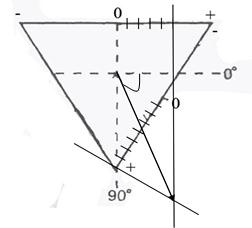
26. На рис. 26 показан треугольник Эйнтховена, в котором обозначена электрическая ось сердца.

26.1. Электрическая ось сердца – это направление суммарного вектора дипольного момента сердца при деполяризации желудочков. Совпадает с анатомической осью сердца.

26.2. В каждый момент времени разность потенциалов в любом отведении равна проекции вектора дипольного момента сердца на ось отведения: 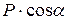. Поэтому отложив эту разность потенциалов на оси отведений и восстановив перпендикуляры к полученным проекциям, на пересечении перпендикуляров можно найти направление электрической оси сердца. 26.3. Не всегда. В ходе цикла сердечного возбуждения направление электрической оси меняется. Это зависит от расположения и числа клеток сердца, которые одновременно находятся в фазе деполяризации или реполяризации. На рис. 26 показано направление электрической оси сердца во время деполяризации желудочков (в норме). 26.4.Не всегда. На рисунке показана нормограмма (угол между электрической осью сердца и осью отведения лежит в пределах от 0 до +90⁰). Бывает также правограмма – отклонение оси сердца вправо ( ) и левограмма – отклонение оси сердца влево ( ).

26.5.

27.На рис.27 приведена запись электрокардиограммы в І и ІІІ стандартных отведениях. В первом отведении сумма зубцов 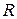и - 6+(-1)=5; в третьем – 10+(-2)=8. Откладываем в сторону положительного полюса отведения соответствующее число единичных отрезков, восстанавливает перпендикуляры к последним. На пересечении их – конец вектора дипольного момента сердца (начало в центре треугольника).