Из истории вопроса 8 страница

Рис. 21

Конкретным материалом экспериментального исследования послужил специально разработанный нами цикл задач-звеньев, в основу построения которого был положен принцип решения одной из известных задач — головоломок. С некоторыми задачами этого цикла мы познакомились уже в предшествующих разделах. Здесь мы приводим их полное систематическое описание.

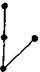
Простейшая и вместе с тем исходная задача этого цикла была названа задачей «трех точек» (I). Условия задачи «трех точек» таковы: соединить три точки двумя прямыми линиями, не пересекая Т-образной преграды (рис. 21).

Второй по порядку задачей была известная нам «4 точки» (II).

Третьей была только что описанная в предшествующем разделе задача «9 точек» (III) ⁴.

Четвертая задача — также знакомая нам — «16 точек» (IV).

Пятая задача — «25 точек» (V): даны 25 точек; требуется провести через эти точки, не отрывая карандаша от бумаги, восемь прямых линий.

Шестая задача — «36 точек» (VI): даны 36 точек; требуется провести через эти точки, не отрывая карандаша от бумаги, 10 прямых линий.

Седьмая задача — «49 точек» (VII): даны 49 точек; требуется провести через эти точки, не отрывая карандаша от бумаги, 12 прямых линий.

Легко заметить, что серия подобных задач может быть продолжена беспредельно. При этом необходимо руководствоваться следующей закономерностью: количество точек должно соответствовать квадратам натурального ряда чисел; количество ли-

⁴ Требование «возвратиться в исходную точку» необходимо лишь для задачи «4 точки». Для всех других задач оно излишне.

ний, которыми необходимо соединить точки, должно возрастать на две, соответственно каждому квадрату. Во всех случаях это количество линий будет составлять предел; меньшим числом, не нарушая требований условия задачи, соединить точки невозможно.

Нужное число линий соответственно избранному количеству точек легко определить, 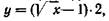пользуясь уравнением

где у — количество линий, а х — количество точек, нарастающее как квадраты натурального ряда чисел (9, 16, 25, 36, 49, 64,81, 100, 122, 144 и т.д.).

Соответственно данной закономерности мы могли использовать задачи: «64 точки» (VIII); «81 точка» (IX); «100 точек» (X); «122 точки» (XI); «144 точки» (XII) и т. д.

В цедом цикл задач можно было рассматривать как сложную познавательную задачу — проблему. Однако эта проблема давалась испытуемым не сразу (например, «144 точки»), а по отдельным задачам — звеньям. Решение первого звена («3 точки») раскрывало исходный принцип («выйти за пределы плоскости, ограниченной точками»), пронизывающий весь последующий путь «восхождения».

Взрослым испытуемым одна за другой предъявлялись задачи данного цикла (I, II, III, IV, V, VI, VII и т. д.) до тех пор, пока испытуемый не вскрывал принцип, удовлетворяющий решению любого звена, т. е. пока не решалась вся сложная познавательная задача.

В других сериях опытов наряду с данной методикой использовались разного рода образующие задачи с последующим учетом их эффективности как по линии прямого, так и по линии побочного продукта.

Прежде всего был прослежен общий ход решения задач данного цикла, т. е. последовательное решение сложной познавательной задачи.

Решение задачи «-<? точки». Наиболее простой в познавательном отношении среди всех прочих задач является задача «3 точки». В этой задаче нахождение решения полностью совпадает с самим решением, поскольку необходимость в какой-либо конкретизации найденного принципа, его уточнения для применения к данным конкретным условиям задачи полностью отсутствует. Эта задача была бы наиболее удачным объектом для изучения интуитивных решений. Однако в этом отношении ей присущ недостаток: принцип выйти за пределы участка плоскости, ограниченного точками, перекрывается более простым приемом — возможностью соединить три точки просто двумя прямыми, не выходя при этом за указанные пределы. Поэтому для образования психологической трудности данная задача нуждается в усложнении условий, выражающемся во введении

Т-образной преграды, исключающей эту перекрывающую данный принцип возможность.

Как правило, задача «3 точки» (с Т-образной преградой) решается без помощи специальной образующей задачи. Дело в том, что, действуя согласно дополнительным ориентирам (Т-образная преграда), испытуемый сам строит в данной ситуации образующую задачу, решение которой совпадает с решением выявляющей задачи, а побочный продукт в таких условиях во

Рис. 22

всех случаях совпадает с прямым продуктом, поскольку, действуя по ориентирам, испытуемый не имеет конкретного замысла плана решения, а ориентиры как бы ведут его к нему.

Наиболее часто решение задачи «3 точки» испытуемыми строится по схеме, изображенной на рис. 22. Вначале используются не две данные линии, а три (одна прямая превращается в ломаную). Концы этой линии соединяются с окончанием преграды (рис. 22, а), затем чертеж принимает вид, изображенный на рис. 22, б, в, и лишь далее, после многих других попыток, находится решение (рис. 22,г).

Если использовать эту задачу в образующей функции и предварить ею «4 точки», то последняя легко решается, даже если образующая задача «3 точки» дается без стимулирующей, т. е. при прямом порядке предъявления. Отсюда следует, что данная задача («3 точки») встает по отношению к задаче «4 точки» в иное отношение, чем все ранее встречавшиеся образующие задачи. Дело в том, что, как мы уже отмечали, конечный маршрут руки испытуемого, являющийся ключом к решению «4 точек», выступает здесь уже не как побочный, а как прямой продукт действия: сама задача «3 точки» выполняет и стимулирующую и образующую функции.

В результате решения задачи «3 точки» испытуемый вырабатывает исходный принцип решения всего цикла задач с нарастающим количеством точек.

Особенностью задачи «3 точки», как мы уже отмечали, является то, что в ее условие вводится дополнение — преграда, конец которой рассматривается испытуемым как дополнительная точка, с которой он и соединяет первую проведенную им линию (по принципу элементарного соединения). Далее, анализируя задачу с помощью элементарного приема (соединение точек по кратчайшему расстоянию), испытуемый приходит к тому, что выравнивает ломаную линию.

После этого поиск организуется за внутренними пределами фигуры, образуемой точками, что дает возможность перенести наличный способ «элементарного объединения» в несколько иные условия. Наконец испытуемый, выделив первый угол как еще одну точку, связывает его с третьей и в результате достигает решения.

Опыт показывает, что если испытуемый не знает принципа решения, то задачу типа «4 точек» он может решить лишь в

Рис. 23

том случае, если имеются ориентиры, лежащие вне фигуры, образуемой прямым соединением точек, в зоне которых испытуемый должен действовать. В данном случае, т. е. когда испытуемый решает задачу «3 точки», наличие преграды, требование обойти преграду приводят к необходимости вырваться за пределы фигуры, образуемой точками, причем удачная попытка закрепляется. Таким образом, вырабатывается способ действия, который затем может быть перенесен на решение задачи «4 точки».

Роль особенностей взаимодействия субъекта с объектом, обусловливающих возможность выработки нового способа действия, отчетливо выступает в том случае, если сравнить задачу «3 точки» с другой, внешне совершенно аналогичной: требуется соединить четыре точки, расположенные, как это изображено на рис. 23, двумя связанными прямыми. В результате этого упражнения никогда нельзя добиться непосредственной выработки способа, при помощи которого испытуемый смог бы решить задачу «4 точки».

Итак, действуя по ориентирам путем «элементарного объединения» в ситуации, детерминирующей особое содержание взаимодействия субъекта с объектом, испытуемый вырабатывает способ действия, как бы впитывающий в себя содержание ситуации, в которой он вырабатывается.

В дальнейших опытах этой серии испытуемого, решившего задачу «3 точки», обращали к следующей задаче — к «4 точкам». Особенности решения этой задачи-звена нами уже неоднократно описывались. Добавим лишь одно: обращаясь к задаче «4 точки», после решения «3 точек» испытуемый почти немедленно находил верное решение, поскольку реализация принципа не составляла в данном случае особого затруднения.

После решения «4 точек» испытуемый обращался к следующей задаче-звену цикла — к «9 точкам».

233

Решение задачи «9 точек». Приведем протоколы решения этой задачи двумя испытуемыми (рис. 24, а, б).

Как видно из протокола, первый испытуемый (В.) нашел решение задачи на 22-й попытке, а испытуемый Н. — на 16-й.

Испытуемым, решившим задачу «9 точек», ставилась задача «16 точек» (в дальнейшем мы будем приводить протоколы решений последующих задач теми же самыми испытуемым) (рис. 25,а,б).

В задаче «16 точек» первый испытуемый (В.) достиг решения на 18-й попытке: второй (Н.) — на 12-й.

Рис. 25

Рис. 26

За задачей «16 точек» следовала задача «25 точек» (рис. 26,а,б).

В этой задаче испытуемый В. достиг решения на 6-й попытке, а испытуемый Н. — на 12-й.

Приводим протоколы решений следующей задачи-звена (рис. 27,а, б).

В случае задачи «36 точек» испытуемый В. добился решения на 10-й попытке, испытуемый Н. — на 7-й.

Задачу «49 точек» испытуемый В. решил на 2-й попытке, испытуемый Н. — на 4-й (рис. 28,а, б).

Задачу «64 точки» оба испытуемых решили с первой попытки (рис. 29,а,б).

Вслед за нахождением решения задачи «64 точки» (с первой же попытки) обоим испытуемым была предъявлена контрольная задача «144 точки» (рис. 30,а,б).

Решение контрольной задачи так же, как и предшествующей, было достигнуто с первой же попытки.

Таким образом, являясь звеном широкой познавательной задачи, каждая задача-звено сама по себе представляет самостоятельную мыслительную задачу. Процесс решения этой задачи, конечный продукт которого становится новой функциональной ступенью развития принципа, сам протекает по внутренним структурным уровням, дифференцируясь на ряд своеобразных процессов взаимодействия, продукты которого становятся условиями внутреннего развития и определяют течение

Рис. 27

новых процессов. Во внутреннем развитии обнаруживается ряд стадий (число которых в разных случаях неодинаково). Наиболее характерны из них следующие: а) рациональное использование результата решения предшествующей задачи; б) отказ от избранного пути и переход к «стихийному» манипулированию посредством элементарных, неосознаваемых эмпирически обобщенных приемов; в) возвращение к исходному принципу («выйти за пределы») — прилаживание рационально используемого принципа посредством неосознаваемых эмпирически обобщенных элементарных процессов; г) решение задачи.

237

Исп. И Рис. 28

И en.В Рис. 29

Рис. 30

Рис. 31

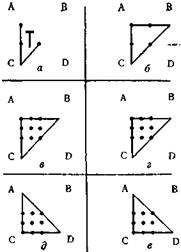
а — результат решений задачи «3 точки»; б — результат решения задачи «4 точки»; о, г -~ первая и вторая попытки решения задачи «9 точек», характерные для одной группы испытуемых (прямой угол в зоне А); д, е — первая и вторая попытки решеннч задачи «9 точек», характерные для другой группы испытуемых (прямой угол в зоне С).

Рассмотрим каждую из этих стадий.

Рациональное использование результата решения предшествующей задачи. У подавляющего большинства испытуемых ориентировка в ситуации каждой следующей задачи-звена на первом этапе определяется прямым продуктом действия в ситуации предшествующей задачи. Иначе говоря, на первом этапе испытуемые, как правило, осуществляют непосредственный перенос этого продукта в условия новой задачи; ранее полученный результат решения выступает теперь как способ решения; продукт переходит в процесс.

В задаче «4 точки» эта первая стадия обычно совпадает с решением и поэтому не выступает здесь со всей отчетливостью. Наиболее характерно эта стадия выявляется при анализе решения задач «9 точек», «16 точек», «25 точек», «36 точек», а иногда и «49 точек», т. е. там, где полученный в решении задачи «3 точки» принцип нуждается в специальной конкретизации.

Так, например, в задаче «9 точек» первые поиски испытуемыми решения этой задачи поразительно однотипны.

В подавляющем большинстве случаев чертежи двух первых попыток оказываются совершенно аналогичными (рис. 31).

Каждый из этих чертежей представляет собой наглядно выраженный перенос результата решения предшествующей задачи.

Следует отметить, что графическое выражение этого переноса имеет некоторое своеобразие по сравнению с попытками решения задачи «4 точки». Это своеобразие состоит в следующем.

Как видно из рис. 31, при выявлении принципа решения в ситуации «3 точек» все испытуемые, подчиняясь особенностям

Рис. 32

а — предшествующее решение задачи «9 точек»; б — первая, вторая и третья попытки решения задачи «16 точек» (вторая группа испытуемых). На рисунке показана лишь небольшая часть вариантов

Рис. 33.

а — решение задачи «19 точек»; б — первые попытки решения задачи «25 точек»

Рис. 34.

й — решение задачи «25 точек»; б — первые попытки решения задачи «36 точек»

Рис. 35.

a — решение задачи «36 точек»; б — первые попытки решения задачи «49 точек»

условий, ориентируют острый угол, образуемый двумя заданными прямыми, в той части пространства, которая выделена нами как зона «С». Точно такую же ориентировку острого угла мы обнаруживаем и в чертеже решения задачи «4 точки». Соответственно этому и прямой угол в чертеже решения данной задачи оказывается сориентированным в зоне «А». При переносе принципа решения задачи «4 точки» в ситуацию «9 точек» наблюдается некоторая вариативность построения чертежа: одна часть испытуемых ориентирует прямой угол точно таким же образом, как это делалось в ситуации «4 точек», т. е. в зоне «А», однако другая часть испытуемых изменяет пространственное ориентирование этого угла, помещая его в зону «С».

Аналогичная картина наблюдается и при анализе решения следующих задач-звеньев (рис. 32—35).

По мере продвижения испытуемых по системе задач-звеньев отмеченная нами вариативность переноса несколько видоизменяется, характер переносимого чертежа стабилизируется. Каждый из испытуемых вырабатывает какой-либо один из двух возможных принципов решения задачи (см. рис. 33—35) и строго его придерживается в дальнейшем. Как показывают данные опытов, переключение испытуемого с одного принципа решения на другой в этих условиях оказывается практически невозможным.

Обнаруженные факты говорят о том, что, получив в итоге решения задачи «3 точки» принцип решения всей цепи задач, испытуемые еще не осознают с полной отчетливостью значимости этого принципа и не вычленяют его из всей совокупности условий ситуации. Недостаточное осознание значимости принципа и проявляется в том, что чертеж решения задачи «4 точки» точно копирует пространственную планировку расположения линий на чертеже решения «3 точек». У некоторых испытуемых это явление распространяется и на решение последующей задачи — «9 точек». Однако другие испытуемые, переходя к решению задачи «4 точки» и достигая этого решения, осознают значимость принципа, с которым им приходится иметь дело. В результате такого осознания испытуемые в какой-то степени абстрагируют этот принцип от конкретных особенностей ситуации и фиксируют его в выражении «необходимо вырваться». В дальнейшем это выражение становится руководством к действию. Рассуждения испытуемых по ходу решения задачи раскрывают, чем мотивируется переориентировка пространственного расположения чертежа решения — испытуемые прежде всего стремятся реализовать условие «необходимо вырваться», поэтому построение чертежа (при решении задачи «9 точек») и начинается в ряде случаев не из точки, находящейся в зоне «А», как это было в ситуации предшествующей задачи («4 точки»), а немедленно выходит за пределы участка, ограниченного точками.

Отказ от избранного пути и переход к «стихийному» манипулированию посредством элементарных, неосознаваемых, эмпирически обобщенных приемов. Первая стадия решения завершается отказом от избранного пути и переходом к тому стихийному манипулированию в участке площади, ограниченном точками, которое чрезвычайно характерно для действий испытуемых, незнакомых с принципом решения предшествующей задачи-звена (эта стадия характерна для задач «9 точек» и «16 точек»).

На рис. 36 приводятся образцы такого манипулирования.

Переход от первой стадии ко второй. Используемый на первой стадии решения мыслительной задачи способ действия, являясь адекватным условию задачи, требует, однако, дополнительной конкретизации и развития, поэтому данный способ действия непосредственно не удовлетворяет особенности ситуации.

Рис. 36.

а — попытки решения задачи «9 точек», б — попытки решения задачи «16 точек»

Новый продукт, возникающий в итоге попытки решения задачи (мы имеем в виду задачу «9 точек»), лишь в первом случае (при первой попытке) отсекает один из возможных вариантов и открывает некоторую (кажущуюся) перспективу (пересечение гипотенузой сразу двух точек), что и осуществляется в следующей попытке. Опирающееся на продукт первой попытки решения последующее действие приводит уже к бесперспективному продукту. Вопрос о путях, по которым осуществляется переход от первой стадии ко второй, еще далеко не выяснен (возможно, что здесь несколько своеобразных путей).

Следует думать, что ведущую роль в этой смене нельзя приписывать ни одному лишь субъекту, ни одному лишь объекту — причиной является именно само взаимодействие субъекта с объектом. .Субъект деформирует исходную ситуацию. Однако эффект этой деформации определяется не только способом действия субъекта, но и особенностями объекта, на который направлено действие, т. е. взаимодействием субъекта и объекта.

Другой характерной особенностью этого перехода является то обстоятельство, что, варьируя чертеж, испытуемые, как правило, не отдают себе ясного отчета о подлинных причинах своих действий, они оценивают лишь их эффект.

Тот факт, что вторая стадия во всех случаях представлена попытками добиться решения путем элементарного объединения точек по кратчайшему расстоянию, не вызывает удивления. Ситуация данной задачи актуализирует у испытуемых лишь один специфический прием. И если этот прием отпадает, его, естественно, заменяет «универсальный метод», который в данном случае «не имеет себе конкурентов».

Возвращение к исходному принципу («выйти за пределы») — прилаживание рационально используемого принципа посредством неосознаваемых эмпирически обобщенных приемов. Вторая стадия обычно завершается после 3—10 попыток. Механизм этой стадии во многом совпадает с механизмом предшествующей. Различия заключаются лишь в способе, которым оперирует субъект. Но, как и на предыдущей стадии, способ второй стадии не приводит к желаемому результату. Действия испытуемого обнаруживают бесперспективность поиска. Динамика ситуации гаснет. Вновь возникает тот критический момент, та некоторая неопределенность в выборе пути дальнейших попыток, некоторая «расшатанность» ситуации, которая характерна для кульминационного момента применения того или иного способа действия, т. е. вновь возникают условия, благоприятствующие смене способа действия.

Как показывают данные экспериментов, на третьей стадии испытуемый вновь использует тот способ действия, которым он уже оперировал на первой стадии. (Как и следовало ожидать, поскольку в опыте большинства испытуемых вообще нет иных способов, которые могли бы быть актуализированы данной ситуацией.) Однако теперь в операциях обнаруживается и нечто новое. Во-первых, уже нет того точного, буквального перенесения чертежа решения предшествующей задачи (хотя в первых попытках этого этапа у некоторых испытуемых такое буквальное перенесение все еще имело место). Видимо, первая и вторая стадии не пропали даром, они способствовали углублению абстракции принципа решения, полученного в предшествующей задаче. На третьей стадии испытуемые руководствуются лишь одним требованием — «вырваться за пределы». Это отчетливо выступает на чертежах попыток решения (рис. 37) — третий этап характеризуется лаконичностью проб, которые нередко состоят всего из двух линий.

Приведем в качестве примера чертежи попыток решения на третьем этапе в условиях задачи «9 точек» (рис. 37). Как видно из чертежей, испытуемый стремится рационально использовать выявившийся принцип решения и ищет его адекватное применение. Однако, не имея специального способа (метода) организации такого поиска, он вновь неосознанно прибегает к «универсальному» приему манипулирования по ориентирам, т. е. прилаживает данный принцип к ситуации задачи посредством неосознаваемых эмпирически обобщенных приемов. Таким

образом, оба использованных ранее способа оказываются объединенными, и это придает качественно иной характер действию, поскольку оно оказывается адекватным данному комплексу условий ситуации.

Третья стадия подготавливает решение, а иногда и завершается им (в том случае, когда решение достигается совершенно внезапно, благодаря удачному стечению обстоятельств). Более подготовленное решение складывается на четвертой стадии.

Решение. Выделение четвертой стадии как относительно самостоятельной оправдывается тем, что способ действия на этой стадии приобретает у некоторых испытуемых иное качество. В определенный момент испытуемый, отправляясь от имевших место процессов манипулирования, начинает не только

Рис. 37

стихийно прилаживать выявившийся принцип, а организует осознаваемый целенаправленный анализ ситуации (особенностью такого анализа является, однако, то, что осознаваемым в нем оказывается лишь оценка полученного результата, а сам процесс продуцирования, как и в предшествующих случаях, остается неосознаваемым).

В ходе такого рода манипуляций наглядный компонент задачи дифференцируется на определенного рода группы точек; путем объединения этих групп элементарным приемом (соединение точек по кратчайшему расстоянию) достигается решение.

Для иллюстрации этого положения проанализируем протоколы опытов.

На чертежах (рис. 38) отчетливо запечатлелись пути анализа испытуемым задачи «16 точек». «Накладывая» на эти точки чертеж решения задачи «9 точек», испытуемый разбил весь комплекс «16 точек» на две подгруппы и объединил их затем путем «элементарного соединения».

Противоположный по форме, но тождественный по своему смыслу факт ясно выступил и в том случае, когда один из испытуемых не смог решить эту задачу самостоятельно.

Приводим протокол опыта.

Решение задачи «9 точек» испытуемому известно.

Задача «4 точки» (рис. 39,а).

Рис. 38. Решение задачи «9 точек» испытуемому известно

Рис. 39

Рис.40

Задача «9 точек» (рис. 39,6).

Испытуемому предлагается задача «16 точек» (рис. 40).

Испытуемый признал задачу нерешаемой.

Предлагается дифференцирующая таблица (рис. 41).

С помощью этой таблицы испытуемый нашел решение при первой же попытке.

С решением задачи «9 точек» испытуемый ознакомился примерно за год до данных опытов и сразу вспомнить его не мог.

®®® ®®®

Рис.41 ®®®

• • • •

Однако «4 точки» были решены испытуемым за 1,5 минуты, после чего на решение задачи «9 точек» испытуемый потратил менее одной минуты (т. е. решение практически наступило «с места»). Затем испытуемому была предложена задача «16 точек». В двух первых попытках испытуемый полностью перенес чертеж решения задачи «9 точек», однако, убедившись в том, что это не приводит к успеху, он отказался от такого переноса и «замкнулся» в участке площади, ограниченном точками. Далее второй стадии решения испытуемый не продвинулся. После

14 неудачных попыток (не выходящих по своему содержанию за пределы второго этапа), потратив на поиски решения 20 минут, испытуемый отказался от задачи, признав ее нерешаемой.

Тогда ему была предложена так называемая дифференцирующая таблица, содержащая те же 16 точек, но с таким изменением: 9 точек (3X3) на этой таблице были нанесены красной тушью, а остальные — черной (см. рисунок дифференцирующей таблицы — рис. 41, приведенный в протоколе опытов с данным испытуемым). С помощью дифференцирующей таблицы испытуемый менее чем через 1 минуту нашел решение («с места»). Опыт показал, чего «не хватало» для решения, что необходимо было увидеть на чертеже и что испытуемый не смог получить самостоятельно, как это было сделано в предшествующем случае.

Характеризуя все выделенные нами стадии в целом, необходимо отметить следующее. Длительность каждой стадии определяется особенностями динамики ситуации. Определенный тип манипулирования сохраняется до тех пор, пока ситуация остается динамичной, т. е. пока сохраняется некоторая вариативность попыток. Как только появляются повторения и новизна, вносимая действием в ситуацию, исчезает, в ходе решения наступает перелом, приводящий либо к отказу от решения, либо к переходу к новой стадии, т. е. к коренному изменению способа действия.

Решение каждой из промежуточных задач-звеньев строится по одному и тому же принципу, с той лишь разницей, что по мере продвижения по цепи задач количество манипуляций постепенно сокращается. Для иллюстрации этой закономерности приводим пример среднего количества попыток, сделанных 30 испытуемыми при решении цепи задач-звеньев.

Таким образом, в большинстве случаев задача «81 точка» решается с первой же попытки. Здесь испытуемые, как правило, по собственной инициативе словесно формулировали принцип решения: «Прежде необходимо вычеркнуть все лишние точки, а затем решить задачу «9 точек». Если после этого испытуемому давалась контрольная задача «144 точки», то она решалась с первой же попытки. У испытуемого складывалась способность решить «с места» любую подобную задачу вне зависимости от избранного количества точек и без опоры на наглядный компонент (в словесном плане), т. е. окончательно вырабатывался принцип решения данной задачи. В проведенных опытах обнаружилась очень большая вариативность показателей у различ-

ных испытуемых. Однако у всех ясно выступила тенденция к снижению числа попыток при переходе к каждой последующей задаче (несмотря на постоянное возрастание объективной сложности задачи). Закономерным оказался и тот факт, что для решения контрольной задачи («144 точки») каждый испытуемый проходил не менее 6—7 предшествующих задач.

Поскольку место каждого звена в ряду данного цикла задач (начиная со второй) определяется чисто объективными количественными зависимостями, решено было исследовать, насколько необходимо при развитии принципа двигаться именно по этой цепи. Для этого надо было выяснить, к чему приведет исключение некоторых отдельных звеньев.

В посвященной этому серии опытов использовалась следующая методика.

Различным группам испытуемых (по пять человек в каждой) были предложены следующие «неполные» циклы задач:

— первый цикл — задачи I, II, IV, V и г. д. (опущена задача «9 точек»).