
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Из истории вопроса 9 страница
— второй цикл — задачи I, II, III, V, VI и т. д. (опущена задача «16 точек»);
— третий цикл —задачи I, II, III, IV, VI, VII и т. д. (опущена задача «25 точек»);
— четвертый цикл —задачи I, II, III, IV, V, VII, VIII и т. д. (опущена задача «36 точек»).
В качестве показателей трудности решения того или иного цикла использовались: во-первых, количество испытуемых, решивших данный цикл (из общего числа группы в пять человек), во-вторых, среднее количество попыток, необходимых испытуемым для решения тех задач-звеньев, которые следовали за пропущенным звеном. Это количество попыток сопоставлялось с теми средними данными, которые были получены при «нормальном» цикле на 30 испытуемых в предшествующей серии опытов.
Результаты, полученные во второй серии опытов, представлены в табл. 1.
Как видно из таблицы, по сравнению с полным циклом трудность сокращенного (неполного) цикла значительно возрастает. Причем первый цикл, в котором была опущена задача «9 точек», оказался самым трудным. В условиях данных опытов (при которых время решения каждого звена ограничивалось 30 минутами) ни один из испытуемых не нашел решения. В остальных циклах по мере удаления опущенной задачи от начала ряда трудность постепенно снижалась.
Таким образом, было установлено, что полный цикл задач представляет оптимальные условия для развития принципа решения. Это положение имело особый интерес, так как объективно принцип решения любой задачи в законченной форме имелся уже в решении задачи «16 точек».
Таблица 1
| Сокращенные циклы | |||||||||
| первый | второй | третий | четвертый | ||||||
| а | б | а | б | а | б | а | б | ||
| «16 точек» «25 » » «36 » » «49 » » | 15—20 12—15 8—10 5-6 | — | Пропущена 3 57 | Пропущена 5 22 | Пропущена 4 14 | ||||
| «64 » » | 2—3 | — | |||||||
| «81 » » | — |
Примечание. 1 — среднее количество попыток решения, имевшее место у 30 испытуемых (данные первой серии опытов); а — количество испытуемых, решивших данный цикл (из 5 человек); б — среднее количество попыток у всех испытуемых, решивших данный цикл.
Однако способ действия, выработанный в результате решения этой задачи, был еще очень ограниченным и непосредственно приводил к успеху только в весьма близкой ситуации (задачи «25 точек»). Действия испытуемых на этой ступени были еще скованы чувственной стороной, они не были достаточно абстрагированы. Для превращения частного способа в принцип необходимо было углубить уровень абстракции, «отфильтровать» действие, объективно выражающее принцип, от направляющих его чувственных элементов ситуации, зачастую случайных. Такая «фильтрация» и осуществлялась в решении последующих задач.
Данные опыты наталкивают на мысль о зависимости выработки принципа решения от включения испытуемого в условия более широкой, или, как мы говорим, перспективной задачи, в которой результат предшествующего решения выступает уже как операция, как способ действия.
Было установлено, что для успешного выявления общего принципа решения задач используемого цикла необходимо, чтобы этот цикл был полным (особенно в его первых 4—5 звеньях). Этот факт нельзя объяснить лишь самим разрывом между задачами.
Пропуск какого-либо звена приводит, конечно, к усложнению условий переноса в связи с увеличением числа возможных вариантов попыток. Это обстоятельство, конечно, играет определенную роль, но данная причина не может быть единственной, поскольку пропуск более отставленных звеньев (начиная от задачи «25 точек» и далее) не вызывает уже у испытуемого особых затруднений в решении очередной задачи сокращенного цикла, хотя объективно сложность каждой последующей задачи увеличивается в геометрической прогрессии. Видимо, важное
значение здесь имеет характеристика самого способа, которым пользуется субъект.
Естественно было предположить, что пропуск тех или других звеньев в начале цепи (пока принцип действия был еще не окончательно выявленным) оказывал столь отрицательное влияние потому, что эти звенья необходимы для выявления принципа и при их выпадении принцип, заключенный в решении предшествующей задачи, оказывался недостаточно выявленным. Это и вызывает иногда непреодолимую трудность при решении последующей задачи. Следовательно, для выявления принципа необходимо включение испытуемого в условия более широкой (перспективной) задачи, однако эта задача не должна содержать в себе слишком большие трудности, связанные с конкретизацией принципа.
Таким образом, в результате проведенных опытов нам удалось выделить одно из условий, способствующих абстрагированию способа действия, а тем самым и развитию принципа решения. Таким условием явилось включение испытуемого в ситуацию перспективной, т. е. более широкой задачи, в которой результат решения предшествующей задачи должен был использоваться как способ решения.
В дальнейших опытах мы исследовали другие условия, также способствующие абстрагированию способа действия от частных элементов конкретной ситуации, в которой это действие было впервые осуществлено.
Раньше нами уже подчеркивалось то обстоятельство, что для осознания использованного в решении практической задачи способа действия, а следовательно, и для выявления принципа решения перед испытуемым должна быть поставлена теоретическая задача. Естественно, что выявление и осознание способа действия в какой-то мере уже предполагает его абстракцию. Отсюда следовало, что постановка теоретической задачи должна явиться одним из условий абстрагирования способа действия.
Для выявления этой зависимости был использован следующий методический прием. Испытуемый имел дело с обычным («полным») циклом задач-звеньев.
Однако первая задача-звено («3 точки») не давалась испытуемому для самостоятельного решения, а объяснялась экспериментатором.
Объяснения проводились примерно так. «Нам дана задача соединить три точки двумя прямыми, не пересекая преграды. Посмотрите: кратчайшим путем этого осуществить нельзя. Используем другую возможность — проведем линию вниз и обойдем преграду».
Непосредственно после такого объяснения решения задачи «3 точки» испытуемому давалась задача «4 точки». Обычная для этой задачи инструкция была видоизменена. Эксперимента-
тор говорил испытуемому: «Теперь дополним три точки еще одной— четвертой — и удалим преграду. Попробуйте соединить все эти точки, не отрывая карандаша от бумаги, так, чтобы ка рандаш возвратился в исходную точку. Что вполне возможно, необходимо лишь дополнить чертеж (соединения трех точек с преградой) в правой верхней части».
Вслед за этим испытуемый без всяких затруднений находил верное решение задачи «4 точки».
Таким образом, испытуемый в какой-то мере знакомился с исходным принципом решения цикла задач-звеньев. Однако поскольку в ситуации данных задач его собственная активность была сведена почти до минимума, можно было предполагать, что выявленный испытуемым принцип был весьма мало абстрагирован от конкретной оболочки ситуации.
После такой подготовки мы вводили в опыт задачу «9 точек», предлагая ее испытуемому для самостоятельного решения.
Всего в этой серии нами было проведено 7 опытов (с 7 испытуемыми). Из этих 7 опытов удалось отобрать 4 случая (4 опыта с 2 испытуемыми), которые удовлетворяли замыслу данных экспериментов.
В указанных 4 случаях испытуемые, сделав по 8—12 безуспешных попыток решить задачу «9 точек», отказались продолжать решение, признав задачу нерешаемой. Сравнивая эти показатели с теми, которые были нами получены в опытах, где активность испытуемых в решении предшествующих задач («3 точки» и «4 точки») ничем не ограничивалась, можно было сделать вывод, что причиной неуспеха испытуемых в данного рода опытах являлось именно ограничение активности.
Поскольку, с нашей точки зрения, лишение испытуемых необходимой для успеха активности оказало отрицательное влияние прежде всего на абстрагирование принципа решения в ситуации предшествующих задач, нами был сделан вывод, что одним из условий успеха такого абстрагирования является активность, самостоятельность действий испытуемого в проблемной ситуации5.
Задача описываемых опытов не сводилась лишь к выявлению фактора активности. Продолжая опыты, мы рассчитывали обнаружить плодотворное влияние на абстрагирование принципа со стороны поставленной перед испытуемым теоретической задачи.
Нам казалось, что, даже действуя в ситуации задачи «9 точек», при определенных условиях испытуемый будет способен
5 Поскольку такой вывод казался нам теоретически очевидным и даже банальным, мы не сочли необходимым дальнейший фактический экспериментальный анализ его посылок (отдавая себе, конечно, отчет в том, что для такого вывода сам по себе полученный нами фактический материал еще не дает достаточного основания).
абстрагировать в какой-то мере тот принцип, который был ему дан в решении предшествующих задач, и если такая абстракция произойдет, она должна будет привести испытуемого к решению задачи «9 точек» (если наше предположение, связывающее неуспех испытуемых с недостаточной абстракцией принципа при решении предшествующих задач, было правильным).
Чтобы придать постановке теоретической задачи максимальную естественность, было решено использовать для этого общение испытуемого с экспериментатором. Беседуя с испытуемыми, отказавшимися продолжать поиски решения «9 точек», экспериментатор просил их дать объяснения только что проделанным неудачным попыткам решения. При этом испытуемым задавался вопрос: «Почему Вы именно так решали задачу?»
В первый момент этот вопрос у всех четырех испытуемых вызывал явное недоумение — ни один из них не смог быстро найти даже какой-либо удовлетворительной мотивировки.
Тогда экспериментатор просил испытуемых объяснить, почему именно так проведена каждая отдельная линия. Испытуемые (все четверо вели себя совершенно одинаково), несколько освоившись с вопросом, начинали придумывать мотивировки, вначале весьма отдаленные, как нам казалось, от истинного положения вещей. Однако таким образом они включились в ситуацию теоретической задачи.
Как показали опыты, такое включение довольно быстро привело к положительному эффекту. Все четверо нашли решение задачи «9 точек» при анализе всего лишь 3—4-го чертежа попыток решения.
При этом испытуемые заявляли, что, думая о том, зачем им понадобилось провести ту или другую линию, они неожиданно замечали, как можно решить задачу. Вместе с тем такое «озарение», по мнению испытуемых, было столь мимолетным, что ответить на вопрос, как все же удалось решить задачу, не было возможности, несмотря на то, что сама задача и ее решение становились для испытуемых совершенно ясными.
Последующие действия этих испытуемых в ситуации дальнейших задач-звеньев цикла показали, что эти действия ничем не отличались от действий испытуемых, решавших цикл обычным путем, т. е. без всякого ограничения активности. Количество попыток решения, допущенное теми и другими категориями испытуемых, было примерно равным. Отсюда следовало, что постановка теоретической задачи привела примерно к тому же эффекту абстрагирования принципа, к которому приводила и активная деятельность испытуемых в ситуации предшествующих задач.
Таким образом, у нас появились основания рассматривать постановку теоретической задачи как одно из условий успеха абстрагирования принципа решения и тем самым его развития.
Для выявления дальнейших условий, способствующих абстрагированию принципа решения, нами был использован переход от третьего звена цикла к четвертому (т. е. от решения задачи «9 точек» к задаче «16 точек»).
Исходя из уже сказанного ранее надо было считать, что успех решения «16 точек» находится в определенной зависимости от степени абстракции принципа решения «9 точек».
Данное положение было прежде всего подтверждено экспериментально. Для этого также был использован метод ограничения активности испытуемых. Однако , если в предшествующих опытах активность испытуемых ограничивалась лишь при решении двух первых задач цикла («3 точки» и «4 точки»), то теперь мы распространили это ограничение и на третью задачу, т. е. на «9 точек». Эта задача, как и предшествующие, не решалась испытуемым активно —• экспериментатор просто показывал ее решение в готовом виде. После такого показа испытуемые должны были решать задачу «16 точек».
Как показали опыты, ни один из испытуемых в таких условиях не смог найти решение «16 точек». Было очевидно, что при показе испытуемым решения задачи «9 точек» никому из них не удалось в достаточной мере абстрагировать принцип ее решения.
Добиться необходимой абстракции этого принципа было бы очень просто, если бы мы решили воспользоваться обучением. Для этого было бы достаточно подсказать испытуемым какую-либо формулировку, например: «Соединяя точки, руководствуйтесь следующим правилом: сначала три вниз, а затем две вбок; можно начинать и с диагонали». Однако нас интересовали вопросы творческого решения, поэтому мы и отыскивали пути, способствующие абстрагированию, которыми бы испытуемый мог воспользоваться без прямого обучения. С таким замыслом был использован следующий методический прием.
Те испытуемые, которые отказались продолжать поиски решения задачи «16 точек», должны были возвратиться к задаче «9 точек», но решать ее не обычным образом, как это делали все прочие испытуемые, а с некоторым видоизменением. Экспериментатор указывал испытуемым расположение и направление первой линии, с которой испытуемый должен был начинать построение чертежа. Несмотря на то что решение задачи «9 точек» было испытуемым уже дано, новое задание оказалось весьма трудно выполнимым. Это подтверждало то, что, зная способ решения, испытуемые еще не владели им полностью.
С целью создания условий для полного овладения этим способом мы предлагали испытуемым выполнить 12 решений задачи «9 точек», используя специальную таблицу (рис. 42). На таблице было нанесено 12 комплексов точек (по 9 точек в каждом) и у каждого комплекса была указана линия, которой необходимо было воспользоваться, начиная построение чертежа.

Рис. 42. Таблица вариантов решения «9 точек»
На выполнение первых 4—5 построений испытуемые затрачивали сравнительно много времени, остальные построения проделыва-лись значительно быстрее. После того как испытуемый выполнял все 12 построений, ему вновь предлагалась задача «16 точек». На этот раз решение «16 точек» наступало очень скоро6.
Такой прием, стимулирующий у испытуемого абстрагирование принципа, оказался весьма эффективным. Это было специально нами показано в опытах с другой группой испытуемых, также состоящей из 5 человек. Новые испытуемые выполняли 12 предваряющих построений вариантов решения «9 точек» еще до того, как им была предложена задача «16 точек» (первые две задачи давались точно так же, как и в предшествующем случае, т. е. с ограничением активности). Все эти 5 испытуемых, выполнивших предварительное построение вариантов решения «9 точек», находили решение «16 точек» после четвертой, иногда пятой попытки. Такой результат был, несомненно, значительно успешнее обычных результатов, с которыми мы сталкивались при «естественном» пути решения цикла (15—20 попыток).
Эффективность описанного приема было решено сопоставить с эффективностью других возможных приемов. Для такого сопоставления были использованы следующие способы.
Необходимо отметить, что некоторые испытуемые в ходе построения различных вариантов решения задачи «9 точек» сами ставили теоретическую задачу, анализировали под ее влиянием ситуацию и словесно формулировали принцип построения. Эти формулировки были различны у каждого испытуемого, но в общем все они напоминали ту, о которой мы уже говорили («сначала три вниз, затем две вбок; можно начинать и с диагонали»).
1. Прием обучения, при котором 5 испытуемым после показа решения «9 точек» (две первые задачи цикла также давались с ограничением активности) сообщалась выявляющая принцип формулировка («две вниз, три вбок; можно начинать и с диагонали»).
2. Прием предварительной автоматизации действия, где 5 испытуемых (при тех же предварительных условиях) раньше, чем приступить к решению задачи «16 точек», должны были 12 раз повторить решение задачи «9 точек», но не из разных положений, т. е. не варьируя чертежа, а повторяя один и тот же его вариант, показанный вначале экспериментатором.
3. Комбинированный прием, в котором сообщение формулировки (первый прием) сочеталось с автоматизацией построения решения в одном варианте (второй прием).
4. Второй комбинированный прием, в котором сообщение формулировки сочеталось с однократным построением двух чертежей решения задачи «9 точек» по двум различным вариантам.
Индикатором эффективности каждого приема служило среднее количество попыток решения задачи «16 точек», предпринятых испытуемыми каждой группы.
Приводим результаты этих опытов, указывая для сопоставления и количество попыток, необходимое для решения задачи «16 точек» при «естественном» прохождении цикла (без ограничения активности и введения каких-либо дополнительных приемов), а также и при условии ограниченной активности в ситуации предшествующих задач, но при приеме предварительного построения 12 различных вариантов решения «9 точек».
1. «Естественный» путь прохождения цикла 15—20
2. Выполнение построения 12 вариантов 4—5
3. При формулировке без дополнительных приемов 30—35
4. Прн автоматизации одного из вариантов 6*
5. Комбинированный прием (формулировка + автоматизация одного варианта) 10
6. Комбинированный прием (формулировка + построение 2 вариантов) 5
* В условиях, когда первая линия проведена экспериментатором.
Отсюда видно, что наиболее эффективным оказался прием, связанный с выполнением построения 12 различных вариантов решения (4—5 попыток), а также и комбинированный прием, при котором словесная формулировка принципа сопровождалась однократным построением двух различных вариантов решения (5 попыток).
Прием автоматизации построения одного из вариантов решения также оказался весьма эффективным (6 попыток), но при оценке его эффективности необходимо принимать во внимание одно важное обстоятельство, встречавшееся в данных опытах,

Рис. 43
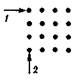
Рис. 44

Рис. 45
на основании которого отмеченная нами эффективность этого приема не может быть непосредственно сопоставляема с эффективностью других приемов. Дело заключается в том, что при автоматизации одного из вариантов решения высокая эффективность достигалась лишь в исключительных обстоятельствах, которые дополнительно создавались экспериментатором. Обстоятельства эти состояли в следующем. В первых опытах было обнаружено, что из пяти испытуемых один нашел решение «16 точек», проделав для этого всего лишь шесть попыток. Три испытуемых вообще не смогли решить «16 точек», а один, последний, проделал для этого более 30 предварительных попыток. Необходимо заметить, что хотя мы автоматизировали у каждого испытуемого лишь один из вариантов решения, вместе с тем у каждого испытуемого эти варианты были различными. Так, у первого автоматизировался вариант № 1 7 (рис. 43, а), у второго — № 2 (рис. 43, б), у третьего — № 3 (рис. 43, в), у четвертого — № 4 (рис. 43, г) и у пятого — № 5 (рис. 43, д).
Оказалось, что испытуемый, решивший «16 точек» всего лишь после шести предварительных попыток, имел дело с вариантом № 3 (рис. 43, в). Причем в первой и второй попытке решения «16 точек» этот испытуемый начинал построение чертежа с крайней верхней левой точки, отмеченной на рис. 44 стрелкой «/», а в дальнейших попытках (вероятно, по случайным обстоятельствам) он перенес начало построения на нижнюю крайнюю левую точку (на рис. 44 отмечена стрелкой «2»). После чего им было найдено решение, выраженное чертежом, изображенным на рис. 45, а.
Мы обратили внимание, что вторая часть его построения, выделенная на рис. 45,а жирными линиями, точно соответство-
7 Варианты нумеруются нами соответственно таблице построения 12 вариантов решения.

Рис. 46. Методика н результат дополнительной серии опытов: [ — автоматизируемые варианты; II — первая линия, проводимая экспериментатором (стрелками указано направление); III — чертежи решения задачи, найденного испытуемым (не. 3 задачу не решил)
вала тому варианту решения «9 точек», который до этого автоматизировался. У других испытуемых таких совпадений не произошло.
Подмеченный факт заставил нас провести дополнительную серию опытов с пятью испытуемыми, которая раскрыла причину этого случая.
Опыты дополнительной серии строились так. Вначале были созданы те же самые условия, что и в предшествующих экспериментах, т. е. испытуемые были ознакомлены с тремя первыми задачами цикла при ограничении активности. Затем, как и в предшествующем случае, у них автоматизировался один из ва-
риантов решения «9 точек» (тот, который был до этого показан экспериментатором). Так, у первого испытуемого автоматизировался вариант № 2 (р,ис. 46, 1а), у второго — № 3 (рис. 46, 16), у третьего — № 5 (рис. 46, /в), у четвертого — № 6 (рис. 46, /г) и у пятого — № 8 (рис. 46, Id). После автоматизации испытуемые обращались к задаче «16 точек». В отличие от предшествующих случаев в этих опытах экспериментатор навязывал испытуемым начало построения чертежа (экспериментатор проводил первую линию сам и лишь затем передавал карандаш испытуемому) (рис. 46, //—б, в, г, д).
Результаты этих onviTOB были таковы. Из пяти испытуемых лишь один не нашел решения задачи. Остальные затратили на поиск очень небольшое количество попыток.
| Испытуемый | Количество попыток |
| 1-й | |
| 2-й | |
| 4-й | |
| 5-й | |
| Среднее количество | 6,5 |
| попыток |
Отсюда следует, что все решения имели строго определенный характер — ранее автоматизированный вариант составлял вторую часть заключительного чертежа. Следовательно, автоматизация действия, которым осуществлялось решение предшествующей задачи, привела к весьма ощутимому эффекту в решении задачи последующей. Однако этот эффект был возможен лишь в особых условиях, где вариативность действий испытуемых была сведена до минимума.
Чтобы окончательно доказать положение о том, что в данных условиях решающее значение имела именно автоматизация действия, мы повторили эти опыты, несколько модифицируя их. Модификация состояла в том, что, сохраняя неизменными все прочие условия, мы исключили автоматизацию построения варианта решения, ограничиваясь лишь его однократной демонстрацией испытуемому.
Из трех человек, принимавших участие в этих контрольных опытах, никто не нашел решения задачи. Таким образом, роль автоматизации способа решения в данных обстоятельствах была окончательно доказана.
Описывая предшествующие серии опытов, мы уже неоднократно отмечали существенное влияние словесной формулировки способа решения предшествующей задачи на успешность действий в ситуации последующей задачи. В новой серии опытов этот вопрос был подвергнут специальному экспериментальному рассмотрению.
Была использована следующая методика. В первой части все испытуемые (в данных опытах участвовали 12 человек, разделенных на 2 группы по б человек в каждой) после беглого показа им решений задачи «3 точки», «4 точки» и «9 точек» дополнительно выполняли построение чертежа четырех различных вариантов решения «9 точек» (варианты 2, 3, 9 и 12 — см. рис. 42).
Представителям первой группы не давалось никаких дополнительных указаний. При построении этими испытуемыми вариантов решения экспериментатор внимательно следил за тем, чтобы оно не сопровождалось попытками словесно формулировать принцип решения задачи. Те испытуемые, у которых подмечалась тенденция к такому формулированию, исключались из опытов. Таким образом, из 13 человек удалось отобрать б, действия которых не имели никаких намеков на попытку словесно формулировать принцип решения.
Представителям второй группы после построения двух первых вариантов решения давалась дополнительная инструкция, требующая словесной формулировки принципа (с помощью экспериментатора).
Таким образом, в начальной части опытов были составлены две группы испытуемых: в первой — построение четырех вариантов решения «9 точек» не сопровождалось словесной формулировкой принципа; во второй — это построение, наоборот, завершалось такой формулировкой.
Заключительная часть опытов проводилась после недельного перерыва и состояла в следующем. 6 испытуемым (по 3 челове-
Т а блица 2
| Категория испытуемых | Задача «16 точек» | Задача «9 точек» | |
| I группа | |||
| Иеп. | 1-й | Нет решения | — |
| » | 2-й | То же | — |
| » | 3-й | » | — |
| » | 4-й | — | Решение после 7 попыток |
| » | 5-й | — | » » 5 » |
| » | 6-й | — | » » 12 » |
| II группа | |||
| Иеп. | 1-й | Решение после 8 попыток | — |
| » | 2-й | » » 13 » | — |
| » | 3-й | » » 10 » | — |
| » | 4-й | — | Решение при 1 попытке |
| » | 5-й | — | » » 2 » |
| » | 6-й | — | » » 1 » |
ка из каждой группы) была дана задача «16 точек» (время для решения ограничивалось десятью минутами). Остальным 6 испытуемым (также по 3 человека из каждой группы) было предложено повторное решение задачи «9 точек».
Результаты опытов приводим в табл. 2.
Из таблицы видно, что испытуемые второй группы (т. е. те, которые словесно формулировали принцип решения задачи «9 точек») в завершающей части опыта обнаружили несравненно больший успех, чем испытуемые первой группы (т. е. те, которые не формулировали словесно принцип решения). Так, например, ни один из испытуемых первой группы в течение 10 минут не смог найти решение «16 точек», в то время как все испытуемые второй группы успешно выполнили это задание; для испытуемых первой группы повторное решение задачи «9 точек» превратилось в проблему, и каждому из них оказалось необходимым сделать в среднем по 8 попыток, в то время как испытуемые второй группы воспроизводили это реиение «с места» (два человека при первой же попытке и один — при второй).
В данном случае мы считаем важным подчеркнуть следующее обстоятельство. Те испытуемые, которые словесно формулировали принцип решения и тем самым знали правило данного действия (например, «два вниз, три вбок; можно начинать и с диагонали»), никогда не сбивались при повторном решении задачи «9 точек». Если же такое правило испытуемому не было дано или не сформулировано им самим, то детали решения «9 точек» очень скоро «забывались», в активной памяти оставался лишь принцип «вырваться»8. Через некоторое время (несколько дней, а может быть, часов и даже минут), повторяя решение задачи, испытуемый уже не может пользоваться ранее найденным решением, он вырабатывает это решение вновь, руководствуясь общим принципом — «вырваться!», и вновь осуществляет конкретизацию этого принципа применительно к ситуации «9 точек» (именно по этой причине испытуемым первой группы и оказывается необходимым при повторном решении задачи «9 точек» проделать в среднем по 8 попыток). В том же случае, если в предшествующем решении задачи способ действия был сформулирован словесно, даже через неделю (а может быть, и через значительно большие сроки) решение задачи не вызывает никакого затруднения — оно не вырабатывается вновь, а воспроизводится в готовом виде.
Таким образом, процесс развития принципа решения задачи выступил как сложный, противоречивый, дискретный процесс, постоянно опосредствующийся взаимодействием субъекта с объектом и вместе с тем направляющий это взаимодействие.
Дата добавления: 2015-02-10; просмотров: 237; Мы поможем в написании вашей работы!; Нарушение авторских прав |