
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ
по дисциплине Основы научных исследований
студенту ИЭиТ З/О института 3 курса 151000.62 специальность
_________________Азизову Руслану Забитовичу_____________________
ТЕМА: Статистическая обработка результатов экспериментов
Вариант № 2
Дата выдачи работы: 23мая 2014 год. Срок сдачи работы: 17 ноября 2014 год.
Руководитель работы _________________ _______________ Шитков А В.
СОСТАВ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ:
1 СТАТИСТИЧЕСКИЕ ОЦЕНКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
1.1 Исходные данные
1.2 Теоретические положения
1.3 Результаты расчетов
2 РАСЧЕТ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ. ОПРЕДЕЛЕНИЕ НЕОБХОДИМОГО ОБЪЕМА ВЫБОРКИ. ОТБРАСЫВАНИЕ ГРУБЫХ НАБЛЮДЕНИЙ
2.1 Исходные данные
2.2 Теоретические положения
2.2.1 Расчет доверительного интервала для математического ожидания
2.2.2 Определение необходимого объема выборки
2.2.3 Отбрасывание грубых наблюдений
2.3 Результаты расчетов
3 ПРОВЕРКА ГИПОТЕЗЫ ОБ ОДНОРОДНОСТИ ДВУХ ДИСПЕРСИЙ. ПРОВЕРКА ОДНОРОДНОСТИ НЕСКОЛЬКИХ ДИСПЕРСИЙ, НАЙДЕННЫХ ПО ВЫБОРКАМ ОДИНАКОВОГО ОБЪЕМА. ПРОВЕРКА ОДНОРОДНОСТИ СРЕДНИХ
3.1 Исходные данные
3.2 Теоретические положения
3.2.1 Проверка гипотезы об однородности двух дисперсий
3.2.2 Проверка однородности нескольких дисперсий, найденных по выборкам одинакового объема
3.2.3 Проверка однородности средних
3.3 Результаты расчетов
4 ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
4.1 Исходные данные
4.2 Теоретические положения
4.3 Результаты расчетов
ЛИСТ ДЛЯ ЗАМЕЧАНИЙ
ОГЛАВЛЕНИЕ
1 СТАТИСТИЧЕСКИЕ ОЦЕНКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
1.1 Исходные данные
Определить для выборки среднее значение, дисперсию, стандартное отклонение, коэффициент вариации, среднюю квадратическую ошибку среднего значения, показатель точности среднего значения и ошибку стандартного отклонения.
Вариант №2
1.2 Теоретические положения
Множество значений случайной величины, полученных в результате эксперимента или наблюдений над объектом исследования, представляет собой статистическую совокупность. Статистическая совокупность, содержащая в себе все возможные значения случайной величины, называется генеральной статистической совокупностью. Выборочной статистической совокупностью называется совокупность, в которой содержится только некоторая часть элементов генеральной совокупности. По результатам экспериментов практически всегда встречаются с выборочной, а не с генеральной совокупностью. Выборочную статистическую совокупность будем в дальнейшем называть выборкой, а число опытов (наблюдений) n , содержащееся в выборке – объемом выборки.
При повторении опытов в одинаковых условиях обычно обнаруживается закономерность в частоте появления тех или иных результатов. Некоторые значения случайной величины появляются значительно чаще других, при этом в целом они группируются относительно некоторого значения - центра группирования, которое мы обозначим через  . Для описания этого явления используется вероятностный подход. Пусть
. Для описания этого явления используется вероятностный подход. Пусть  - вероятность того, что случайная величина, являющаяся результатом эксперимента, примет значение
- вероятность того, что случайная величина, являющаяся результатом эксперимента, примет значение  ,
,  Если значения
Если значения  известны для всех возможных значений
известны для всех возможных значений  из генеральной совокупности, то величину
из генеральной совокупности, то величину  можно найти по формуле
можно найти по формуле

Величину  называют математическим ожиданием или генеральным средним случайной величины. Одно только математическое ожидание не может отобразить все характерные черты статистической совокупности.
называют математическим ожиданием или генеральным средним случайной величины. Одно только математическое ожидание не может отобразить все характерные черты статистической совокупности.
Исследователю необходимо знать, кроме того, изменчивость, или вариацию наблюдаемой характеристики объекта.
Рассеивание случайной величины относительно математического ожидания характеризуется величиной, называемой дисперсией. Обычно она обозначается через  . Для генеральной совокупности дисперсия определяется по формуле
. Для генеральной совокупности дисперсия определяется по формуле

Дисперсию  часто называют генеральной дисперсией. Квадратный корень из дисперсии называется средним квадратическим отклонением случайной величины, или стандартом
часто называют генеральной дисперсией. Квадратный корень из дисперсии называется средним квадратическим отклонением случайной величины, или стандартом  .
.

Как и дисперсия, среднее квадратическое отклонение является характеристикой рассеивания значений случайной величины относительно математического ожидания.
Формулы справедливы для дискретных случайных величин. Для непрерывных случайных величин математическое ожидание и дисперсия выражаются через соответствующие интегралы.
Поскольку экспериментатор встречается не с генеральной совокупностью, а с выборкой, необходимо иметь формулы, позволяющие приближенно оценить математическое ожидание  и дисперсию
и дисперсию  на основе экспериментальных данных.
на основе экспериментальных данных.
Пусть по результатам однородной серии опытов получена выборка  . Наилучшей оценкой для математического ожидания
. Наилучшей оценкой для математического ожидания  является среднее арифметическое или просто «среднее»
является среднее арифметическое или просто «среднее»

Найденное значение  называют еще выборочным средним в отличие от генерального среднего
называют еще выборочным средним в отличие от генерального среднего  . Оценкой дисперсии
. Оценкой дисперсии  случайной величины является выборочная, или эмпирическая дисперсия. Она обозначается через
случайной величины является выборочная, или эмпирическая дисперсия. Она обозначается через  и вычисляется по формуле
и вычисляется по формуле

Числитель этой формулы представляет собой сумму квадратов отклонений значений случайной величины от среднего значения  . Знаменатель формулы для выборочной дисперсии называется числом степеней свободы, связанным с этой дисперсией, и обозначается через
. Знаменатель формулы для выборочной дисперсии называется числом степеней свободы, связанным с этой дисперсией, и обозначается через 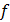 :
:

Величина

является оценкой среднего квадратического отклонения  выборки.
выборки.
Ее также называют выборочным стандартом или стандартным отклонением выборки.
Часто для оценки изменчивости (вариации) случайных величин используют коэффициент вариации  . Он равен отношению
. Он равен отношению  к
к  , %:
, %:

Коэффициент вариации характеризует не абсолютное, а относительное рассеивание случайной величины относительно среднего.
Важное значение имеют также следующие статистические показатели:
средняя квадратическая ошибка среднего значения
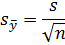
показатель точности среднего значения

ошибка среднего квадратического отклонения

* Для вычисления среднего арифметического значения  и выборочной дисперсии
и выборочной дисперсии  и стандартного отклонения выборки
и стандартного отклонения выборки  в Microsoft Excel можно воспользоваться встроенными статистическими функциями, соответственно СРЗНАЧ, ДИСП и СТАНДОТКЛОН.
в Microsoft Excel можно воспользоваться встроенными статистическими функциями, соответственно СРЗНАЧ, ДИСП и СТАНДОТКЛОН.
1.3 Результаты расчетов
Таблица 1. - расчетный лист из Microsoft Excel части №1.
2 РАСЧЕТ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ. ОПРЕДЕЛЕНИЕ НЕОБХОДИМОГО ОБЪЕМА ВЫБОРКИ. ОТБРАСЫВАНИЕ ГРУБЫХ НАБЛЮДЕНИЙ
2.1 Исходные данные
«Расчет доверительного интервала для математического ожидания.
Определение необходимого объема выборки.
Отбрасывание грубых наблюдений»
Вариант №2
1) Определить доверительный интервал для математического ожидания при уровне значимости  .
.
2.1) Определить необходимый объем выборки, при котором среднее значение отличалось бы от математического ожидания не более чем на  с доверительной вероятностью
с доверительной вероятностью  .
.
2.2) Определить необходимый объем выборки при уровне значимости  и относительной допускаемой ошибке
и относительной допускаемой ошибке  .
.
2.3) Проверить, являются ли минимальное и максимальное значения выборки промахом при уровне значимости  .
.
2.2 Теоретические положения
2.2.1 Расчет доверительного интервала для математического ожидания
Величина среднего арифметического значения  , найденная по выборке, представляет ценность постольку, поскольку по ней можно судить об истинном среднем, математическом ожидании
, найденная по выборке, представляет ценность постольку, поскольку по ней можно судить об истинном среднем, математическом ожидании  . Представляет интерес отыскание величины максимальной ошибки
. Представляет интерес отыскание величины максимальной ошибки  , которую мы допускаем, предполагая
, которую мы допускаем, предполагая  равным
равным  . Требуется, следовательно, найти величину при которой
. Требуется, следовательно, найти величину при которой

Этим неравенством задается интервал, в котором находится значение математического ожидания  . Этот интервал называется доверительным интервалом для математического ожидания. Величина
. Этот интервал называется доверительным интервалом для математического ожидания. Величина  зависит от объема выборки n. Чем больше n , тем меньше максимальная ошибка
зависит от объема выборки n. Чем больше n , тем меньше максимальная ошибка  . Однако, даже при заданном n нельзя абсолютно достоверно указать величину
. Однако, даже при заданном n нельзя абсолютно достоверно указать величину  , так как расчет этой величины, как и любой статистический вывод, делают на основе результатов эксперимента, а они заведомо содержат ошибки. Выводы, которые делают на основе неточных данных, принципиально не могут быть абсолютно достоверными. Поэтому говорят о надежности статистического вывода, которую оценивают величиной доверительной вероятности p , где
, так как расчет этой величины, как и любой статистический вывод, делают на основе результатов эксперимента, а они заведомо содержат ошибки. Выводы, которые делают на основе неточных данных, принципиально не могут быть абсолютно достоверными. Поэтому говорят о надежности статистического вывода, которую оценивают величиной доверительной вероятности p , где  . Например, статистический вывод, сделанный с доверительной вероятностью
. Например, статистический вывод, сделанный с доверительной вероятностью  , будет справедлив в 95 случаях из 100. Будем пользоваться чаще величиной
, будет справедлив в 95 случаях из 100. Будем пользоваться чаще величиной  , называемой уровнем значимости. Уровень значимости задается заранее, до проведения расчетов. Типичные значения для q : 0,01; 0,05 и 0,1 или, в процентах: 1, 5, 10.
, называемой уровнем значимости. Уровень значимости задается заранее, до проведения расчетов. Типичные значения для q : 0,01; 0,05 и 0,1 или, в процентах: 1, 5, 10.
Величина  определяется по формуле
определяется по формуле  , следовательно, доверительный интервал для математического ожидания равен
, следовательно, доверительный интервал для математического ожидания равен

где  – стандартное отклонение выборки;
– стандартное отклонение выборки;
 - табличное значение
- табличное значение  - критерия Стьюдента;
- критерия Стьюдента;
 - объем (количество элементов) выборки.
- объем (количество элементов) выборки.
Величину  - критерия Стьюдента определяют из соответствующих таблиц (они имеются практически в каждом руководстве по математической статистике или планированию эксперимента) ее следует выбирать по предварительно заданному уровню значимости
- критерия Стьюдента определяют из соответствующих таблиц (они имеются практически в каждом руководстве по математической статистике или планированию эксперимента) ее следует выбирать по предварительно заданному уровню значимости  и числу степеней свободы
и числу степеней свободы  .
.
Оценку для математического ожидания в виде интервала часто называют интервальной оценкой.
Не следует думать, что во всех случаях целесообразно задаваться возможно большей надежностью статистического вывода. С большей надежностью можно гарантировать только более широкий доверительный интервал для математического ожидания при тех же опытных данных.
2.2.2 Определение необходимого объема выборки
Пусть требуется найти минимальное число n повторений опытов, при котором среднее арифметическое  , найденное по этой выборке, отличалось бы от математического ожидания не более чем на заданную величину
, найденное по этой выборке, отличалось бы от математического ожидания не более чем на заданную величину  .
.
Это, по существу, задача, обратная предыдущей. Для ее решения необходимо знать оценку дисперсии  . Здесь можно использовать, например, результаты проведенных ранее исследований (разведывательных опытов). Искомое значение n определяется по формуле
. Здесь можно использовать, например, результаты проведенных ранее исследований (разведывательных опытов). Искомое значение n определяется по формуле

При проведении экспериментальных исследований необходимое число наблюдений в опыте определяют по формуле

где  - коэффициент вариации (определяется по результатам проведенных ранее исследований), %;
- коэффициент вариации (определяется по результатам проведенных ранее исследований), %;
 - показатель точности, %.
- показатель точности, %.
Обычно показатель точности  принимают равным 5 %. Величину уровня значимости
принимают равным 5 %. Величину уровня значимости  выбирают равной 0,05, при этом
выбирают равной 0,05, при этом  или 0,01 и
или 0,01 и  .
.
При статистической обработке данных широко используют процедуры проверки статистических гипотез. Статистическая гипотеза – это некоторое предположение относительно свойств генеральной совокупности, проверяемое по выборке. Например, гипотеза об однородности средних или дисперсий, законе распределения и т. д. Проверка статистической гипотезы – это процедура, по результатам которой гипотеза принимается или отбрасывается.
Выдвинутую гипотезу называют основной, или нулевой. Гипотезу, противоречащую нулевой, называют конкурирующей. Для проверки нулевой гипотезы используют специально подобранную случайную величину, распределение которой известно. Ее называют статистическим критерием. Например, при проверке гипотезы об однородности дисперсий в качестве критерия используют отношение выборочных дисперсий, которое подчиняется статистическому распределению Фишера. Для проверки статистической гипотезы вычисляют значения критерия по имеющимся опытным данным. Если оно находится внутри некоторой заданной заранее области, называемой областью принятия гипотезы (областью допустимых значений), то нулевая гипотеза принимается. В противоположном случае значение критерия попадает в критическую область, и тогда гипотеза отвергается.
Однако попадание критерия в область допустимых значений не дает права категорически утверждать, что гипотеза полностью подтвердилась.
Можно только заключить, что по данным выборки значение критерия не противоречит гипотезе. Поэтому, принимая решение о правильности гипотезы, можно допустить ошибку. Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле верна. Вероятность этой ошибки задается заранее выбором уровня значимости q . (Как указывалось, типичные значения q :0,01; 0,05; 0,1 или 1, 5 и 10%.) Ошибка второго рода состоит в том, что гипотеза принимается, а на самом деле она неверна. Уменьшение ошибки второго рода достигается увеличением уровня значимости. Таким образом, уменьшение уровня значимости приводит к уменьшению ошибки первого рода и при этом к увеличению ошибки второго рода. Необходимо отметить, что единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объема выборок.
2.2.3 Отбрасывание грубых наблюдений
Грубые наблюдения (промахи) подлежат исключению из выборки. Для их обнаружения можно вновь воспользоваться  - критерием Стьюдента. В этом случае сомнительный результат
- критерием Стьюдента. В этом случае сомнительный результат  , временно исключают из выборки, а по оставшимся данным рассчитывают среднее арифметическое
, временно исключают из выборки, а по оставшимся данным рассчитывают среднее арифметическое  и стандартное отклонение выборки
и стандартное отклонение выборки  . Далее вычисляют величину
. Далее вычисляют величину
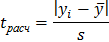
Из таблиц распределения Стьюдента по выбранному уровню значимости  и числу степеней свободы
и числу степеней свободы 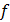 , находят табличное значение
, находят табличное значение  - критерия
- критерия  . Если
. Если  , то подозреваемый результат является промахом и должен быть исключен из выборки.
, то подозреваемый результат является промахом и должен быть исключен из выборки.
Иногда сомнение вызывают одновременно два или даже три элемента выборки. Исследование начинают с того из сомнительных элементов, значение которого ближе к среднему арифметическому выборки, а остальные сомнительные элементы временно отбрасывают. Затем рассчитывают значения  и
и  выборки без исключенных элементов, а также значение
выборки без исключенных элементов, а также значение  для оставшегося сомнительного элемента. Далее решают вопрос об исключении этого элемента с уровнем значимости
для оставшегося сомнительного элемента. Далее решают вопрос об исключении этого элемента с уровнем значимости  . Если
. Если  , то оставшийся элемент выборки отбрасывают как грубое измерение. Тем более грубымибудут и остальные, ранее исключенные элементы. Если наименее сомнительный элемент не оказался промахом
, то оставшийся элемент выборки отбрасывают как грубое измерение. Тем более грубымибудут и остальные, ранее исключенные элементы. Если наименее сомнительный элемент не оказался промахом  , то его присоединяют к выборке и исследуют следующий сомнительный элемент, и т.д.
, то его присоединяют к выборке и исследуют следующий сомнительный элемент, и т.д.
*Примечание.
Для вычисления среднего арифметического значения  и стандартного отклонения выборки
и стандартного отклонения выборки  в Microsoft Excel можно воспользоваться встроенными статистическими функциями СРЗНАЧ и СТАНДОТКЛОН. При определении табличного значения критерия Стьюдента используют функцию СТЬЮДРАСПОБР
в Microsoft Excel можно воспользоваться встроенными статистическими функциями СРЗНАЧ и СТАНДОТКЛОН. При определении табличного значения критерия Стьюдента используют функцию СТЬЮДРАСПОБР 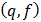 . Для поиска максимального и минимального элемента
. Для поиска максимального и минимального элемента  используют встроенные статистические функции МАКС и МИН. При вычислениях в ячейки содержащие эти элементы помещают текст.
используют встроенные статистические функции МАКС и МИН. При вычислениях в ячейки содержащие эти элементы помещают текст.
2.3 Результаты расчетов
Таблица 2...4. - расчетный лист из Microsoft Excel части №2
3 ПРОВЕРКА ГИПОТЕЗЫ ОБ ОДНОРОДНОСТИ ДВУХ ДИСПЕРСИЙ. ПРОВЕРКА ОДНОРОДНОСТИ НЕСКОЛЬКИХ ДИСПЕРСИЙ, НАЙДЕННЫХ ПО ВЫБОРКАМ ОДИНАКОВОГО ОБЪЕМА. ПРОВЕРКА ОДНОРОДНОСТИ СРЕДНИХ
3.1 Исходные данные
«Проверка гипотезы об однородности двух дисперсий.
Проверка однородности нескольких дисперсий, найденных по выборкам одинакового объема. Проверка однородности средних»
Вариант №2
1) Для сравнения точности двух электровлагомеров каждым из них проведено 10 измерений влажности одного и того же участка доски. Результаты замеров влажности W, %, первым и вторым прибором следующие:
| Первый прибор | ||||||||||
| Второй прибор |
На основании приведенных данных проверить, являются ли расхождения в точности исследуемых приборов значимыми.
2) На станке обработано пять однородных заготовок. Для каждой полученной детали в шести точках замерялась ее толщина.
| № детали | Толщина, мм, в зависимости от номера точек замеров | |||||
| 50,43 | 50,38 | 50,19 | 50,28 | 50,43 | 50,24 | |
| 50,41 | 50,47 | 50,27 | 50,28 | 50,14 | 50,53 | |
| 50,12 | 50,29 | 50,07 | 50,14 | 50,33 | 50,46 | |
| 50,54 | 50,35 | 50,26 | 50,02 | 50,35 | 50,37 | |
| 50,46 | 50,37 | 50,51 | 50,49 | 50,43 | 50,40 |
Требуется выяснить, можно ли считать, что разброс значений толщин для всех деталей одинаков.
3) Сравнивалась шероховатость поверхностей двух деталей. Для каждой было получено 10 значений шероховатости Rz , мкм.
| Деталь №1 | ||||||||||
| Деталь №2 |
Требуется выяснить, является ли различие между шероховатостями двух деталей значимым.
3.2 Теоретические положения
3.2.1 Проверка гипотезы об однородности двух дисперсий
Результаты экспериментальных исследований часто используют, например, для сравнения условий функционирования объектов, оценки сравнительной эффективности различных технологий, разных способов измерения и т. д. Во многих случаях соответствующие выводы делают на основе анализа и сравнения нескольких выборок. Одна из простых задач такого типа возникает, когда надо сравнивать точность двух измерительных приборов. В этом случае, очевидно, следует сравнить оценки дисперсий соответствующих выборок.
Пусть имеются две выборки объемом  , по которым найдены выборочные дисперсии
, по которым найдены выборочные дисперсии  . Они являются оценками для генеральных дисперсий соответственно
. Они являются оценками для генеральных дисперсий соответственно  . Предположим, что
. Предположим, что  . Требуется выяснить, можно ли утверждать, что обе выборки взяты из одной и той же генеральной совокупности. Ее это так, то
. Требуется выяснить, можно ли утверждать, что обе выборки взяты из одной и той же генеральной совокупности. Ее это так, то  . В этом случае выборочные дисперсии
. В этом случае выборочные дисперсии  называются однородными, а различие между ними объясняется влиянием случайных ошибок. В противном случае генеральные дисперсии
называются однородными, а различие между ними объясняется влиянием случайных ошибок. В противном случае генеральные дисперсии  не равны друг другу. Тогда говорят, что различие между выборочными дисперсиями значимо.
не равны друг другу. Тогда говорят, что различие между выборочными дисперсиями значимо.
Для проверки статистической гипотезы об однородности двух дисперсий используется F - критерий Фишера. Вначале вычисляется величина  , равная отношению большей из выборочных дисперсий к меньшей. Пусть
, равная отношению большей из выборочных дисперсий к меньшей. Пусть  .
.
Тогда

Далее задаются уровнем значимости  и вычисляют числа степеней свободы дисперсий числителя и знаменателя по формуле:
и вычисляют числа степеней свободы дисперсий числителя и знаменателя по формуле:  и
и  . По трем величинам
. По трем величинам  таблиц распределения Фишера отыскивают величину
таблиц распределения Фишера отыскивают величину  . Если
. Если  , то выборочные дисперсии считаются неоднородными (различие между ними значимо) для выбранного уровня значимости
, то выборочные дисперсии считаются неоднородными (различие между ними значимо) для выбранного уровня значимости  . Если
. Если  ,, то можно принять гипотезу об однородности дисперсий.
,, то можно принять гипотезу об однородности дисперсий.
3.2.2 Проверка однородности нескольких дисперсий, найденных по выборкам одинакового объема
Для проверки однородности нескольких дисперсий при равных объемах всех рассматриваемых выборок  может быть использован G - критерий Кохрена.
может быть использован G - критерий Кохрена.
Пусть 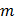 - количество выборочных дисперсий, однородность которых проверяется. Обозначим эти дисперсии
- количество выборочных дисперсий, однородность которых проверяется. Обозначим эти дисперсии  . Вычисляется расчетное G - отношение по формуле
. Вычисляется расчетное G - отношение по формуле

В числителе этой формулы стоит наибольшая из рассматриваемых дисперсий, а в знаменателе – сумма всех дисперсий. Далее обращаются к таблицам распределения Кохрена. По выбранному уровню значимости q , числу степеней свободы каждой выборки  и по количеству выборок
и по количеству выборок 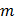 из этой таблицы отыскивают величину
из этой таблицы отыскивают величину  . Если
. Если  то можно принять гипотезу об однородности дисперсий. В противном случае она отвергается.
то можно принять гипотезу об однородности дисперсий. В противном случае она отвергается.
3.2.3 Проверка однородности средних
Здесь исследуются две выборки, имеющие различные средние арифметические. Данная проверка позволяет установить, вызвано ли расхождение между средними случайными ошибками измерения или оно связано с влиянием каких-либо неслучайных факторов. Эта процедура находит широкое применение, например, в случаях, если требуется установить идентичность параметров одинаковых изделий, изготавливаемых на разном оборудовании.
Проверка проводится с применением 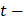 критерия Стьюдента. Пусть
критерия Стьюдента. Пусть  объемы выборок,
объемы выборок,  соответствующие средние,
соответствующие средние,  оценки дисперсий, найденные по этим выборкам.
оценки дисперсий, найденные по этим выборкам.
Предстоит рассмотреть два случая.
1. Дисперсии  однородны.Вычисляется расчетное
однородны.Вычисляется расчетное  отношение по формуле
отношение по формуле

Из таблиц распределения Стьюдента при уровне значимости  и числе степеней свободы
и числе степеней свободы  находят табличное значение
находят табличное значение  . Если
. Если  , то расхождение между средними значимо. В противном случае можно принять гипотезу об однородности средних. Формула упрощается, если обе выборки имеют одинаковый объем, т. е.
, то расхождение между средними значимо. В противном случае можно принять гипотезу об однородности средних. Формула упрощается, если обе выборки имеют одинаковый объем, т. е.  . В этом случае
. В этом случае
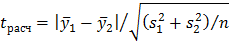
2. Дисперсии  неоднородны.Как и в предыдущем случае здесь можно использовать
неоднородны.Как и в предыдущем случае здесь можно использовать 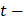 критерий Стьюдента, но формула для расчета имеет уже следующий вид:
критерий Стьюдента, но формула для расчета имеет уже следующий вид:

Далее вычисляют величину 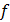 по формуле
по формуле

Найденное значение 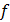 округляют до целого и принимают за число степеней свободы. По этой величине и по уровню значимости
округляют до целого и принимают за число степеней свободы. По этой величине и по уровню значимости  из таблиц распределения Стьюдента отыскивается
из таблиц распределения Стьюдента отыскивается  . Дальнейший ход проверки не отличается от предыдущего случая.
. Дальнейший ход проверки не отличается от предыдущего случая.
*Примечание.
Табличное значение критерия Фишера определяют, используя встроенную статистическую функцию FРАСПОБР  .
.
3.3 Результаты расчетов
Таблица 5...7. - расчетный лист из Microsoft Excel части №3.
4 ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
4.1 Исходные данные
«Проверка гипотезы о нормальности распределения»
Вариант №2
В результате проведения разведывательных опытов была получена выборка. Проверить гипотезу о нормальности распределения.
4.2 Теоретические положения
«Проверка гипотезы о нормальности распределения»
Предположение о том, что выходная величина подчиняется нормальному закону распределения, можно проверить разными способами. Наиболее строгим из них является применение критерия  Пирсона. Для этого необходимо иметь выборку достаточно большого объема:
Пирсона. Для этого необходимо иметь выборку достаточно большого объема:  . Диапазон изменения выходной величины в этой выборке разбивается на
. Диапазон изменения выходной величины в этой выборке разбивается на  интервалов так, чтобы эти интервалы покрывали всю ось от
интервалов так, чтобы эти интервалы покрывали всю ось от  до
до  и в каждый интервал при этом попало не менее пяти значений выходной величины. Подсчитывают количество
и в каждый интервал при этом попало не менее пяти значений выходной величины. Подсчитывают количество  , наблюдений, попавших в каждый интервал. Затем вычисляют теоретические вероятности попадания случайной величины в каждый
, наблюдений, попавших в каждый интервал. Затем вычисляют теоретические вероятности попадания случайной величины в каждый  интервал. Для этого используют формулу
интервал. Для этого используют формулу


где  - среднее арифметическое выборки;
- среднее арифметическое выборки;  - среднее квадратическое отклонение выборки;
- среднее квадратическое отклонение выборки;  - нижняя граница
- нижняя граница  го интервала;
го интервала;  верхняя граница
верхняя граница  го интервала;
го интервала;  нормированная функция Лапласа:
нормированная функция Лапласа:

Значения ее для  и
и  определяются из специальных таблиц, которые приведены во многих справочных и учебных пособиях по теории вероятностей и математической статистике. При отыскании значений этой функции для отрицательных аргументов следует иметь ввиду, что функция Ф(z) нечетная:
определяются из специальных таблиц, которые приведены во многих справочных и учебных пособиях по теории вероятностей и математической статистике. При отыскании значений этой функции для отрицательных аргументов следует иметь ввиду, что функция Ф(z) нечетная:

Для вычисления теоретических вероятностей попадания случайной величины в каждый  й интервал можно воспользоваться формулой
й интервал можно воспользоваться формулой

Следующим этапом является вычисление величины  по формуле
по формуле

По выбранному уровню значимости  и числу степеней свободы
и числу степеней свободы  из таблиц распределения
из таблиц распределения  выбирают величину
выбирают величину  . Гипотезу о нормальности распределения можно принять, если
. Гипотезу о нормальности распределения можно принять, если 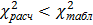 .
.
Менее строгой и поэтому не часто применяемой является проверка нормальности распределения по критерию Колмогорова.
4.3 Результаты расчетов
Таблица 8. - расчетный лист из Microsoft Excel части №3.
Дата добавления: 2015-02-10; просмотров: 220; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Управление кредитным риском | | | Методологические характеристики исследования |