Линейный закон фильтрации (закон Дарси)

Первые исследования по движению жидкости в пористых телах были произведены в середине девятнадцатого века французским инженером-гидравликом Анри Дарси (Darcy), который наблюдал течение воды в песчаных фильтрах водоочистных сооружений в связи с водоснабжением города Дижона.

В своих опытах Дарси применял прибор, состоящий из вертикального цилиндрического сосуда, заполненного слоем песка, через который при различных давлениях между входом и выходом пропускался поток воды в направлении сверху в низ (рис 1.4.1). Изменяя высоту, толщину слоя, состав песка и измеряя расход воды, Дарси в 1856 году установил, что расход несжимаемой жидкости (воды) Q пропорционален потере гидростатического напора жидкости h и площади поперечного сечения сосуда F и обратно пропорционален высоте слоя грунта L:

. (1.4.1)

Рис. 1.4.1. Схема опыта Дарси.

Гидростатический напор определим, исходя из рис 1.4.1:

,

но P₁=ρgh₁ и P₂=ρgh_2, следовательно,

и (1.4.2)

где Р₁ и Р₂ гидростатическое давление столбов жидкости высотой h₁ и h₂.

Запишем формулу (1.4.1) в виде равенства:

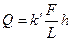(1.4.3)

с учетом (1.4.2):

и

(1.4.4)

Здесь – так называемый коэффициент фильтрации, который характеризует как фильтрационные свойства среды, так и физические свойства фильтрующей жидкости (в данном случае - воды). Из (1.4.3) следует, что коэффициент фильтрации имеет размерность:

[k’^’]=м/с,

т. е. размерность скорости.

Но Дарси проводил свои исследования только с водой. В дальнейшем, при исследовании фильтрации других жидкостей различной вязкости, было установлено, что коэффициент фильтрации обратно пропорционален кинематической вязкости жидкости:

.

Тогда была введена новый коэффициент к так, что

или 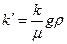, (1.4.5)

где - динамическая вязкость, - плотность жидкости. Ускорение свободного падения g введено для удобства из соображений размерности,

Подставляя (1.4.5) в (1.4.4), имеем:

. (1.4.6)

Здесь Q - объемный расход жидкости в единицу времени; - скорость линейной фильтрации; F - площадь фильтрации; - динамическая вязкость жидкости; Р - перепад давления; L - длина пористой среды; k – коэффициент проницаемости или пропускной способности среды:

(1.4.7)

Размерность k в системе СИ определим из (1.4.7): [k]=м².

Таким образом, физический смысл проницаемости можно объяснить пропускной способностью породы, а именно той площадью поперечного сечения, которое способно пропустить через себя жидкость или газ.

Уравнение (1.4.7) можно переписать следующим образом:

(1.4.8)

Здесь - скорость фильтрации жидкости в пористой среде, которая в соответствии с уравнением (1.4.8) пропорциональна градиенту давления и обратно пропорциональна динамической вязкости:

Итак, в международной системе СИ за единицу проницаемости в 1м² принимается проницаемость такой пористой среды, при фильтрации через образец которой площадью 1 м² и длиной 1 м при перепаде давления 1 Па расход жидкости составляет 1 м³/сек.

Используется также внесистемная единица проницаемости - Дарси (Д):

1Д - это проницаемость такой пористой среды, при фильтрации через образец которой площадью 1 см² и длиной 1 см при перепаде давлений 1 атм (кгс/см²) расход жидкости вязкостью 1 сПз составляет 1 см³/сек.

Учитывая, что 1 сПз = 1мПа^.с, 1 атм = 10⁵Па, получим 1Д = 10^-12 м².

Полученная формула (1.4.8) является лишь частным случаем линейного закона фильтрации Дарси. В общем случае трехмерного потока ее следует записать в виде:

или (1.4.9)

Последнее выражение закона Дарси в обобщенном виде учитывает наклон пласта, по которому течет флюид плотностью r, к горизонту под углом j, тогда