
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка гипотезы о равенстве среднего числовому значению
Проверка статистической гипотезы
Проверка гипотезы о равенстве среднего числовому значению
Понятие “статистическая гипотеза” более емкое, чем просто оценка значения неизвестного параметра. С помощью статистического эксперимента мы хотим проверить гипотезу о том, что неизвестное среднее m равно некоторому значению m0. Эта гипотеза будет основной. При этом альтернативной ей может быть гипотеза m¹m0или более сложная гипотеза типа m<m0или m>m0. Например, известно, что в среднем за смену на станке производится 110 деталей. Станок сломался и его “отремонтировали”. Получив на “отремонтированном” станке показатели за n смен, мы хотим проверить гипотезу: “производительность станка не изменилась”, когда альтернативной гипотезой является, что она изменилась, или что производительность станка увеличилась, или что производительность станка уменьшилась.
При решении таких задач также применяется аппарат построения для соответствующей статистики области Ib, вероятность попадания в которую b достаточно близка к 1. При попадании статистики, построенной по выборке, в эту область принимается основная гипотеза (в нашем примере, что производительность станка не изменилась и равна 110); в противном случае, если значение статистики попало в область, противоположную Ib, принимается альтернативная гипотеза (производительность станка изменилась). В задачах о проверке гипотез принято область, противоположную Ib, называть критической, а число a = 1–b – уровнем значимости. Уровень значимости a обычно берут равным 0,05, иногда 0,01. При a = 0,05 мы, проверяя на деле истинную гипотезу о том, что m = m0, будем ее отбрасывать с вероятностью 0,05, т.е. в среднем 5 из 100 истинных гипотез. В простых случаях областями Ibоказываются уже знакомые нам доверительные интервалы. При проверке гипотезы Q = Q0мы строим с доверительной вероятностью b = 1–a при альтернативной гипотезе Q ¹ Q0двусторонний, а при гипотезах Q > Q0и Q < Q0односторонние с нижней границей хни верхней границей хвдоверительные интервалы. Если этот интервал покры-вает Q0, гипотеза Н0принимается, если не накрывает – отвергается. Приведем некоторые примеры.
Пример 4.1.В задаче про “ремонт” станка проверяем гипотезу об изменении производительности станка, если за 31 смену получены данные о производительности станка, для которых  = 100, s2= 202= 100. Уровень значимости a = 0,05 (b = 0,95) и n = n – 1 = 30. Значения tn;b, участвующие в построении доверительного интервала, отыскиваются в таблице 6, b или a в верхней строке:
= 100, s2= 202= 100. Уровень значимости a = 0,05 (b = 0,95) и n = n – 1 = 30. Значения tn;b, участвующие в построении доверительного интервала, отыскиваются в таблице 6, b или a в верхней строке:

Вывод.Гипотеза о том, что производительность станка не изменилась, не проходит на уровне значимости 5 %, так как старая производительность, равная 110, в 95-процентный доверительный интервал, построенный по новой средней производительности, не попала. Более того, она не попала бы в доверительный интервал, даже если бы мы задались 98-процентным уровнем доверия, для которого t30;0,98= 2,46 (I0,98= 100 ± 8,98). Т.е. наша выборка показала, что гипотеза о том, что производительность станка не изменилась, не проходит даже на уровне значимости 2 %. Только при уровне доверия 0,99 (t30;0,98= 2,75) интервал становится таким большим (I0,99= 100 ± 10,04), что мы уже не можем быть на 99% уверены, что изменение выработки не случайно. Увидев, что новые показатели хуже старых, берем в качестве альтернативной гипотезу о том, что новое среднее меньше старого (такая альтернатива естественна, если  ) то есть, что производи-тельность станка уменьшилась. Это предположение подтверждается даже на уровне значимости 0,01. Действительно, строим односторонний доверительный интервал для уровня доверия 0,99. Значения tn;b, участвующие в построении одностороннего доверительного интервала, отыскива-ются в таблице 6, b или a в нижней строке:
) то есть, что производи-тельность станка уменьшилась. Это предположение подтверждается даже на уровне значимости 0,01. Действительно, строим односторонний доверительный интервал для уровня доверия 0,99. Значения tn;b, участвующие в построении одностороннего доверительного интервала, отыскива-ются в таблице 6, b или a в нижней строке:

Так как m0= 110 не входит в построенный односторонний интервал, можно принять гипотезу о том, что производительность уменьшилась, на уровне значимости 1%.
Перечислим критерии, по которым, не привлекая понятия доверительного интервала, прове-ряется статистическая гипотеза о том, что среднее значение генеральной совокупности m = m0на уровне значимости a (они выведены из формул для двустороннего и одностороннего доверитель-ного интервала для уровня доверия b = 1–a).
Вычисляем по выборке значение статистики
 .
.
1. Критическая область для односторонней проверки гипотезы, что среднее значение гене-ральной совокупности m = m0по сравнению с альтернативой m ¹ m0, на уровне значимости a опре-деляется неравенством:
|T| > tn–1;a
(tn–1;aотыскивается по таблица 6 критических значений распределения Стьюдента, a в верхней строке).
2. Критическая область для односторонней проверки гипотезы, что среднее значение генеральной совокупности m = m0по сравнению с альтернативой m > m0, на уровне значимости a определяется неравенством:
T > tn–1;a
(tn–1;aотыскивается по таблице 6 критических значений распределения Стьюдента, a в нижней строке)
3. Критическая область для односторонней проверки гипотезы, что среднее значение генеральной совокупности m = m0по сравнению с альтернативой m<m0, на уровне значимости a определяется неравенством:
T < –tn–1;a
(tn–1;aотыскивается по таблице 6 критических значений распределения Стьюдента, a в нижней строке).
Если вычисленное значение статистики Т попадает в критическую область, то основная гипо-теза отвергается. Вероятность попадания в эту область равна принятому уровню значимости a.
В этом случае принимается альтернативная гипотеза.
В нашем примере про станок Т = –2,74, а t30;0,01= 2,58, так что основная гипотеза не проходит, а проходит альтернативная гипотеза m < 110 при уровне значимости 0,01.
Использование доверительного интервала для параметра в задачах проверки гипотезы о его значении имеет то преимущество, что для случая, когда основная гипотеза не проходит, этот метод сразу дает эмпирическую оценку параметра. В качестве значения параметра конкурирующей гипотезы часто берут эмпирическое значение параметра (в частности, в качестве а можно взять 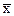 ). В нашем случае такой оценкой для новой производительности станка будет число 100.
). В нашем случае такой оценкой для новой производительности станка будет число 100.
Дата добавления: 2015-04-11; просмотров: 363; Мы поможем в написании вашей работы!; Нарушение авторских прав |