Выявление погрешностей наблюдений

Для отдельного поста наблюдений связь между среднегодовой концентрацией примеси q_k и среднеквадратичным отклонением σ_k выражается линейным уравнением регрессии:

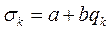. (1.15)

Коэффициенты a и b определяются по формулам:

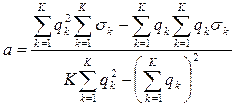; (1.16)

. (1.17)

В случае, если q_k = 0 в уравнении (1.15) σ_k также принимается равной нулю.

Коэффициент b при отсутствии ошибок измерений, т.е. при a = 0, представляет собой коэффициент вариации концентрации примеси V_k = σ_k/q_k и является показателем достоверности данных. При наличии погрешностей измерений коэффициент a является средней квадратичной ошибкой наблюдений, отношение a/σ – ее относительным значением, а ε = |a/b| – средней абсолютной ошибкой.

Не менее важным показателем правильности измерений является коэффициент корреляции r между σ_k и q_k:

. (1.18)

В зависимости от значений r и b а также их сочетаний устанавливается надежность характеристик рассматриваемого ряда:

1. При r > 0,7 и 0,8 < b < 1,5 погрешность a/σ, как правило, меньше 0,2; результаты измерений концентрации примеси следует считать достоверными с малой погрешностью измерений, которая не сказывается на средних характеристиках.

2. При r > 0,5 и b < 1 погрешность a/σ составляет 0,2 – 0,4; результаты измерений содержат случайные ошибки.

3. При 0,5 < r < 0,7 и b < 0,5 погрешность a/σ > 0,4; это возможно при некотором завышении концентраций примеси в случайных ошибках.

4. При r < 0,5 и b < 0,5 погрешность a/σ > 0,4; это обусловлено наличием случайных или систематических погрешностей в измерениях в течение некоторого периода наблюдений; данные наблюдений вызывают сомнение.