Класификационные и ординационные методы изучения сообществ и экосистем

При изучении экосистем или отдельных сообществ с целью биоиндикации требуется:

1) определить пространственные границы экосистемы (или сообщества);

2) выявить и описать зависимость ценотических характеристик, значимых для биоиндикации, от факторов среды, лимитирующих биоту или конкретное соощество.

Эти задачи решаются, соответственно, методами классификации (1) и ординации (2).

Классификационный подходпредполагает, что изучаемые сообщества (экосистемы) пространственно более или менее четкие пространственные границы, в пределах которых однородны и достоверно отличаются от соседних сообществ (экосистем). Целью классификационных методов математического анализа является выделение этих относительно дискретных сообществ (экосистем) и их пространственных границ. Ординационный подход (от лат. "ordino" – упорядочивать), наоборот, игнорирует границы сообществ (экосистем) или даже предполагает их отсутствие. Ординационные методы выявляют количественные закономерности изменений характеристик популяций и сообществ в градиентах среды.

На самом деле, у различных природных экосистем естественные границы могут быть выражены в разной степени: и очень контрастно, и довольно слабо, и практически отсутствовать (если наблюдается непрерывное пространственное изменение параметров сообщества).

Так, некоторые экосистемы и сообщества, действительно, относительно дискретны. Это, в первую очередь, биогеоценозы – экосистемы, локализованные в биотопах (участках территории или акватории со специфическими условиями среды, относительно однородными внутри самого биотопа и значительно отличающимися от внешних условий). Многие консорции также имеют довольно чёткие границы. Как правило, дискретные многовидовые биосистемы характеризуются сравнительно высокой целостностью, сложной сетью многообразных межвидовых связей и значительной эмерджентностью свойств, и поэтому должны изучаться с позиций холизма (см.: Шуйский, 2001, стр. 35–37). Примерами таких биосистем могут служить малое непроточное озеро или лесная опушка (биогеоценозы), небольшой обособленный коралловый риф или друза двустворчатых моллюсков, формирующие своей жизнедеятельностью специфическую местную среду и, следовательно, особые сообщества –консорции. Подобные биосистемы хорошо поддаются классификации и плохо – ординации (т.к. их внутренняя среда довольно однородна).

Если же биота (или конкретное сообщество) существует в пространственно неоднородных, разнообразных абиотических условиях (например, морская сублитораль, прерия, и др.), то, как правило, связи между отдельными видами оказываются сравнительно слабыми. Эти формации складываются пассивно, вследствие простого наложения картин пространственного распределения популяций отдельных видов, образующих единый экологический континуум (состояние биоты, при котором виды распределяются независимо и непрерывно). Для изучения подобных биосистем более эффективны редукционистские методы (Шуйский, 2001, стр. 36–37). Ясно, что такие внутренне неоднородные экосистемы (или сообщества) без четких пространственных границ плохо поддаются классификации и хорошо – ординации.

Большинство природных экосистем занимают промежуточное положение. Очень широко варьирует степень выраженности их границ, внутренней неоднородности, межвидовых взаимодействий, эмерджентность свойств. Поэтому при биоиндикационных экологических исследованиях обычно наиболее плодотворным оказывается сочетание классификационного и ординационного подходов.

Классификационные методы позволяют преодолеть субъективность выделения исследователем границ экосистем (сообществ), количественно оценить степень их выраженности благодаря математическому подходу. Наиболее объективную классификацию могут дать методы кластерного анализа (от англ. "cluster" – группа, гроздь), группирующие объекты в классы (кластеры) таким образом, чтобы объекты, входящие в один класс, были более однородными, сходными по сравнению с объектами, входящими в другие классы. При этом сопоставляться может как видовой состав сообществ (т. наз. нумерический кластерный анализ), так и их различные количественные характеристики. В последнее время многие экологи предпочитают использовать нумерический кластерный анализ, поскольку: 1) само присутствие или отсутствие того или иного вида очень информативно; 2) обнаружить факт присутствия особей вида гораздо проще, чем правильно определить количественные характеристики популяции или сообщества (для чего требуются гораздо более трудоемкие методы пробоотбора); 3) результат классификационного анализа по количественным характеристикам во многом определяется тем, какие именно показатели исследователь считает важными и учитывает в расчетах, в то время как нумерическая классификация всегда использует один и тот же признак.

Нумерический кластерный анализ может осуществляться как для сравнения отдельных станций наблюдения (Q-анализ, оценивающий сходство видового состава сообществ на разных станциях), так и для отдельных видов (R-анализ, оценивающий сходство пространственного распределения различных видов). Из многих индексов, характеризующих степень сходства видового состава сообществ на разных станциях (или, наоборот, сходства пространственного распределения видов) наиболее прост и популярен коэффициент Съёренсена:

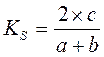
где при Q-анализе a и b – количество видов в двух сравниваемых сообществах (или на двух сравниваемых станциях), c – количество видов, общих для обеих сообществ (обеих станций)

Для количественных данных (при R-анализе) аналогичный показатель носит название коэффициента Чекановского K_CZ и имеет вид:

где x_1i и x_2i – значения показателя обилия (плотность или биомасса популяции) i-го вида в описаниях 1 и 2; min (x_1i ; x_2i ) – наименьшее из двух сравниваемых значений данного показателя обилия.

При кластерном анализе по количественным признакамстепень сходства сообществ оценивается по "расстояниям" между ними в евклидовом пространстве учитываемых признаков (чаще всего это – евклидовы расстояния). Такими признаками являются различные количественные характеристики сообществ, имеющие биоиндикаторное значение (разд. 3.2.3). Результаты анализа наглядно выражаются графически в виде гистограмм – схем, показывающих, на каких уровнях проявляется сходство между разными объектами.

Кластерный анализ очень широко используется в различных областях науки как средство типологического анализа. Однако результативность кластерного анализа по количественным характеристикам ограничивается более или менее субъективным выбором признаков (за исключением нумерического анализа), алгоритмов кластеризации и методов интерпретации результатов (в частности, исследователь сам решает, какой именно уровень сходства следует принять для выделения сообществ).

Для отнесения результатов одиночных измерений к одному из выделенных классов данных полезен также многомерный дискриминантный анализ (не являющийся строго классификационным методом). Он позволяет не только более обоснованно принимать решения по классификации, но и более объективно выбирать её критерии. Применение дискриминантного анализа может быть весьма эффективным, но оно ограничено высокими требованиями к репрезентативности материала.

Ординационные методыпозволяют установить зависимость характеристик биоты от факторов среды. Они осуществляют упорядочивание объектов (например, станций наблюдения, характеризуемых соответствующими значениями биоиндикаторных признаков сообществ) вдоль каких-либо осей (пространственных градиентов, факторов среды, оси времени и т.д.).

Наиболее простым и высокоэффективным методом ординации является прямой градиентный анализ. Суть его сводится к выявлению изменения величин обилия видов по градиентам лимитирующих факторов среды. По факторам, обнаружившим достоверное воздействие на биоту, далее проводится регрессионный анализ. Приемы прямого градиентного анализа эффективно применяются в тех ситуациях, когда лимитирующие факторы известны и сравнительно немногочисленны.

Экологами широко используются также методы непрямой ординации, в частности, двумерное шкалирование (метрическое и неметрическое) и многомерное шкалирование.

Методы метрического шкалирования включают: анализ главных компонент (МГК); анализ главных координат (principal coordiates analysis), анализ соответствия (correspondence analysis; расстояние оценивается по критерию хи–квадрат); бестрендовый анализ соответствия (detrended correspondence analysis), и др.

Методы неметрического шкалирования включают: собственно неметрическое шкалирование (численное значение переменной заменяется ее рангом); нелинейное, или немонотонное, шкалирование; ассиметричный матричный анализ (asymmetric matrix analysis); метод развертки (unfolding); анализ траекторий (path analysis), выявляющий причинные связи между переменными, и др.

Методы многомерного шкалирования включают: канонические корреляции (canonical correlations); “Прокрустов анализ”(Procrustes analysis); множественный анализ соответствия; шкалирование индивидуальных расстояний (individual distance scaling); шкалирование с граничными условиями (constrained scaling); трехмерную развертку (3‑way unfolding); непараметрический тест (random skewer analysis), и др.

Применение методов непрямой ординации иногда оказывается очень эффективным, однако требует от эколога большого опыта и чувства меры. Абстрактное представление причинно-следственных связей (в отличие от прямой ординации) ограничивает четкость интерпретации результатов анализа, создает опасность их ошибочной трактовки.