
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интеграла.
Определенный интеграл
Понятие определенного интеграла. Свойства определенного
интеграла.
Пусть на отрезке  задана функция
задана функция  . Разобьем отрезок
. Разобьем отрезок  произвольным образом точками
произвольным образом точками  на n частичных отрезков длиной
на n частичных отрезков длиной  . Выберем внутри каждого частичного отрезка точку
. Выберем внутри каждого частичного отрезка точку  (рис.1.). Найдем значение функции
(рис.1.). Найдем значение функции  в точках
в точках  .
.
 | |||
|
Интегральной суммой функции  на отрезке
на отрезке  называется сумма вида:
называется сумма вида:
 (2)
(2)
Геометрически  представляет собой алгебраическую сумму площадей прямоугольников, в основаниях которых лежат частичные отрезки
представляет собой алгебраическую сумму площадей прямоугольников, в основаниях которых лежат частичные отрезки  , а высоты равны
, а высоты равны  (рис. 1).
(рис. 1).
Определение: Определенным интегралом от функции  на отрезке
на отрезке  называется предел интегральной суммы (2), найденный при условии, что длина наибольшего из частичных отрезков стремится к нулю:
называется предел интегральной суммы (2), найденный при условии, что длина наибольшего из частичных отрезков стремится к нулю:
 (3)
(3)
Свойства определенного интеграла:
1)  (4)
(4)
2)  (5)
(5)
3)  (6)
(6)
4)  (7)
(7)
5) Если  , то
, то
 (8)
(8)
6) Если 

 (9)
(9)
7) Если  , то
, то
 (10)
(10)
8) Если  непрерывна на
непрерывна на  , то на этом отрезке существует хотя бы одна точка
, то на этом отрезке существует хотя бы одна точка  ,
,  , такая, что верно равенство
, такая, что верно равенство
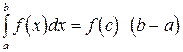 (11)
(11)
9) Если  непрерывна и
непрерывна и  , то имеет место равенство
, то имеет место равенство
 (12)
(12)
10) Если  - какая-либо первообразная функции
- какая-либо первообразная функции  , справедливо равенство:
, справедливо равенство:
 (13)
(13)
Формула (13) называется формулой Ньютона-Лейбница.
11) Если  - четная функция, то
- четная функция, то
 (14)
(14)
12) Если  - нечетная функция, то
- нечетная функция, то
 (15)
(15)
Дата добавления: 2015-04-11; просмотров: 205; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| ДЛЯ КОНТРОЛЯ ЗНАНИЙ СТУДЕНТОВ II КУРСА | | | Требования к уровню освоения дисциплины |