
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Виды математических моделей ИСО
Рассмотрим виды математических моделей только в одном аспекте, который обусловливает принципиальные различия математических моделей и методов отыскания на них оптимальных решений.
Вид модели определяется типом связи между решениями (альтернативами, стратегиями) и результатами, который в свою очередь зависит от условий, в которых протекает операция и приходится принимать решения.
1. Решения принимаются в условиях определенности. Это значит, что каждому решению можно поставить в соответствие (пусть даже путем сложных расчетов) определенный результат, то есть имеет место детерминированный тип связи. Модели, описывающие такие ситуации, называются детерминированными. Этот тип модели на практике применяется наиболее широко, так как он "удобен в работе". По этой причине такие модели часто используют в качестве первого приближения и в условиях, отличающихся от ситуации определенности.
2. Решения принимаются в условиях риска. Между решениями и результатами имеет место стохастическая связь: определенному решению может соответствовать более одного результата, вероятности появления которых известны. Адекватным отображением таких условий являются вероятностные(стохастические)модели. Если под результатом имеется в виду значение критерия, то исходная постановка задачи (и модель) некорректна: нельзя максимизировать или минимизировать случайную величину. В этом случае в качестве критерия следует выбирать не исходный показатель, а одну из его вероятностных характеристик, например, математическое ожидание или дисперсию. Неоднозначность обусловлена наличием случайных факторов. Но осреднение случайных аргументов и осреднение результатов, на которые первые влияют, далеко не всегда одно и то же. Это объясняется тем, что в общем случае не выполняется равенство
М[f(x1, x2, ..., xn)] = f[M(x1), M(x2), ..., M(xn)], (1.1)
где xj- случайные величины, М -знак математического ожидания.
Рассмотрим пример такой ситуации. Пусть фирма "Апельсин" постоянно занимается продажей фруктов. Для простоты будем считать, что поставка и продажа фруктов осуществляется целыми контейнерами, а единицей времени является неделя. Спрос на фрукты С колеблется случайным образом, но вероятность спроса в случайно взятую неделю Р(С)известна. При заключении договора с поставщиком на очередной период фирма должна определить наиболее выгодное для нее количество контейнеров, которое будет поставляться еженедельно, если известны прибыль от реализации одного контейнера dи убыток bпри его невостребовании. Так как спрос случаен, то и результат - доход за неделю D для фиксированного числа заказываемых контейнеров пбудет случайной величиной: в случае, когда спрос превысит предложение, то есть при С>п,
D=dn; (1.2)
если же предложение окажется выше спроса (С<п),доход
D=dn-(n-C)b. (1.3)
Таким образом, доход Dявляется функцией управляемой величины пи случайного фактора С. Очевидно, что максимизация такого показателя бессмысленна. В качестве критерия оптимальности разумно взять математическое ожидание дохода за неделю, так как его максимизация обеспечит максимум дохода за весь период. Поскольку вероятность появления случаев (1.2) и (1.3) определяется P(С), то модель задачи будет иметь вид
M[D]=  =
= 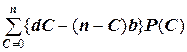 +
+ 
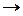 max, (1.4)
max, (1.4)
n>0,int, (1.5)
где intозначает "целое". При составлении этой модели в явном виде учитывалась стохастичность ситуации и, следовательно, принимаемые по ней решения в такой же степени учитывают фактор случайности. Упрощенное представление операции может базироваться на аппроксимации реальной ситуации детерминированной. В этом случае спрос рассматривается как неслучайная величина, равная его математическому ожиданию  . При этом доход
. При этом доход
D= 
также неслучаен. На такой модели оптимальное решение, максимизирующее D, определяется просто: п0=С.
Чтобы показать отличие результатов при использовании упрощенной модели и модели (1.4), произведем расчет для исходных данных d=30, b=5и вероятности спроса:
| C | |||||||
| P(C) | 0,1 | 0,25 | 0,3 | 0,25 | 0,1 |
Вычисляем средний спрос: С=  =3. Тогда по упрощенной модели получим: п0=3,D=90. Такой доход имел бы место при детерминированном и неизменяемом уровне спроса. Но при случайном спросе величина D=90 будет достигаться только в те недели, когда спрос окажется не меньше 3, а в другие недели доход будет ниже и, следовательно, средний доход за весь период станет меньше 90. Чтобы показать это и одновременно определить оптимальное число контейнеров при случайном спросе, вычислим значения среднего дохода по модели (1.4) при всех возможных п:
=3. Тогда по упрощенной модели получим: п0=3,D=90. Такой доход имел бы место при детерминированном и неизменяемом уровне спроса. Но при случайном спросе величина D=90 будет достигаться только в те недели, когда спрос окажется не меньше 3, а в другие недели доход будет ниже и, следовательно, средний доход за весь период станет меньше 90. Чтобы показать это и одновременно определить оптимальное число контейнеров при случайном спросе, вычислим значения среднего дохода по модели (1.4) при всех возможных п:
| n | |||||

| 56,5 | 74,25 | 81,5 |
По результатам вычислений видно, что решение n0=3, полученное на детерминированной модели, не обеспечивает максимального среднего дохода. Кроме того, видно, что в условиях случайного спроса оптимальным является решение п=4, при котором средний доход составляет 81.5 против 74.25 при n0=3. Это пример операции, для которой не выполняется равенство (1.1), хотя случайный фактор имеет симметричное распределение. Судя по разнице результатов на двух моделях, в данной операции стохастичность оказывает значимое влияние и поэтому ее нельзя не учитывать.
Однако наличие случайных факторов не всегда влечет за собой неоднозначность результатов. Возможны случаи, когда элементарные составляющие процесса или системы ведут себя случайно, а результаты системы в целом не случайны. Характерным примером такой системы является идеальный газ, поведение которого подчиняется детерминированному закону Бойля-Мариотта. Неслучайное поведение на макроуровне при наличии элементов случайности на микроуровне называют стохастическим детерминизмом.
3. Решения принимаются в условиях неопределенности. Это ситуация, противоположная первой рассмотренной. Природа неопределенности может быть различной, но в общем случае она проявляется в том, что определенному решению соответствует более одного результата, а вероятностные характеристики результатов неизвестны. Математические модели, описывающие неопределенный тип связи, разнообразны и не имеют единого названия. В частности, к этому классу относятся матричные модели, модели типа "игра", "аукционный торг", нечеткие модели.
Во многих случаях ситуацию неопределенности можно представить (или аппроксимировать) матрицей вида
| Альтер-нативы | Состояние среды | |||
| Q1 | Q2 | … | Qn | |
| A1 | u11 | u12 | … | u1n |
| A2 | u21 | u22 | … | u2n |
| … | … | … | … | |
| Am | um1 | um2 | … | umn |
где uij- результат (исход) выбора альтернативы Аiпри условии, что среда окажется в состоянии Qj; uijможет иметь смысл прибыли, дохода, выигрыша или затрат, проигрыша, убытков и т.п.).
Прежде чем выбирать решение на этой модели, нужно определиться с принципом оптимальности, на основе которого будут сравниваться альтернативы, так как только одно желание ЛПР получить наилучший результат не дает такой основы. Принцип оптимальности зависит от точки зрения на ситуацию ЛПР, его отношения к риску, от предположений относительно поведения среды. Наиболее характерной гипотезой поведения среды является представление, что среда ведет себя наихудшим образом ("как назло"). Это самый пессимистический взгляд на ситуацию, свойственный ЛПР, не склонному к риску. В этом случае выбор решения основывается на принципе гарантированного результата(иногда его называют критерием Вальда). Он состоит в том, что эффективность каждой альтернативы оценивается наихудшим из исходов, возможных при выборе данной альтернативы. Такой результат гарантируется, то есть будет не хуже, при любом фактическом состоянии среды. Теперь очевидно, что наилучшим решением в смысле принятого принципа оптимальности будет выбор той альтернативы, которая имеет наилучший гарантированный результат. Так, если uijимеет смысл прибыли, то оценкой i-й альтернативы является  uij, а оптимальной будет альтернатива, максимизирующая эту величину, то есть Ai,на которой достигается
uij, а оптимальной будет альтернатива, максимизирующая эту величину, то есть Ai,на которой достигается 
 uij. Применительно к этой ситуации принцип гарантированного результата называют принципом максимина,а оптимальную альтернативу - максиминной. В условиях неопределенности только этот принцип имеет объективное обоснование и дает абсолютно надежную оценку.
uij. Применительно к этой ситуации принцип гарантированного результата называют принципом максимина,а оптимальную альтернативу - максиминной. В условиях неопределенности только этот принцип имеет объективное обоснование и дает абсолютно надежную оценку.
Другой подход, называемый также критерием Сэвиджа, использует аналогичный прием, но по отношению к преобразованной матрице - матрице риска (сожалений) [rij], где rij=  uij-uij, то есть риск - это разность между максимально возможным выигрышем при j-м состоянии среды и выигрышем при выборе i-й альтернативы в условиях незнания о фактическом состоянии среды. Так как цель состоит в уменьшении риска, то, используя принцип минимакса(гарантированного риска), определим как оптимальную ту альтернативу, на которой достигается
uij-uij, то есть риск - это разность между максимально возможным выигрышем при j-м состоянии среды и выигрышем при выборе i-й альтернативы в условиях незнания о фактическом состоянии среды. Так как цель состоит в уменьшении риска, то, используя принцип минимакса(гарантированного риска), определим как оптимальную ту альтернативу, на которой достигается 
 uij, тогда риск не превысит этой величины ни при каком состоянии среды.
uij, тогда риск не превысит этой величины ни при каком состоянии среды.
Гибкий учет отношения ЛПР к риску возможен с помощью критерия Гурвица. Если исходы имеют смысл дохода, то оптимальная альтернатива определяется из условия
 {g
{g  uij +(1-g)
uij +(1-g)  uij},
uij},
где g=[0, 1] - коэффициент риска. При ориентации на самое худшее g=0,что соответствует критерию Вальда, а для крайнего оптимиста g=1. Промежуточные значения gотражают разный уровень риска ЛПР.
Возможны и другие подходы к выбору оптимальных решений в условиях неопределенности, но все они, как и последние два, не гарантируют достижение расчетных результатов.
Как следует из вышерассмотренного, выбор вида модели требует от исследователя интуиции и опыта наряду с глубокими знаниями моделируемой области. Следует особо отметить, что построение модели основывается на представлениях аналитика, которые могут не соответствовать реальным связям в большей или меньшей степени. При этом большое значение имеют оценка влияния случайных факторов, факторов неопределенности, уровень агрегирования, допустимая сложность модели. Так, нередко возникает дилемма: построить высокоточную, но очень сложную модель, на которой можно будет получить только приближенное к оптимальному решение, либо поступиться точностью моделирования и иметь возможность применять на модели точные методы оптимизации. Какое решение окажется ближе к истинному оптимальному, заранее сказать невозможно. К сожалению, не существует готовых рецептов построения математических моделей. Это один из этапов операционного исследования, который, следуя Саати, можно отнести к области искусства.
Дата добавления: 2015-04-11; просмотров: 275; Мы поможем в написании вашей работы!; Нарушение авторских прав |