
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематика материальной точки. Механика –это раздел физики, изучающий простейшие формы движения тел в пространстве и времени.
Раздел 1. Механика
Механика –это раздел физики, изучающий простейшие формы движения тел в пространстве и времени.
Механическое движение – это изменение положения тел или их частей в пространстве относительно друг друга с течением времени.
Интуитивные представления о понятиях пространства и времени имеет каждый человек на основании повседневного опыта.
Пространство — это совокупность отношений, выражающих взаимное расположение материальных объектов друг относительно друга (расстояния между ними и ориентацию).
Основные свойства пространства: трёхмерность, плоскостность, непрерывность, однородность и изотропность. Однородность - означает физическое равноправие всех точек в пространстве. Изотропность - физическое равноправие всех направлений в пространстве.
Под временем понимается свойство материальных процессов иметь определенную длительность, следовать друг за другом в определенной последовательности.
Основные свойства времени: непрерывность, одномерность, однородность.
Положение тела в пространстве может быть определено только по отношению к каким-либо другим телам. Это же относится и к движению тела, поэтому любое движение относительно, а значит необходимо ввести понятия системы отсчета.
Система отсчета (СО) – это совокупность тела отсчета, системы координат и часов (либо любого прибора ведущего отсчет времени).
Тело отсчета – это тело, относительно которого рассматривается движение других тел.
Система координат – совокупность фиксированных направлений в пространстве. Как правило, используется правовинтовая декартова система координат.
Движения реальных тел очень сложны, поэтому чтобы упростить возможность описания их движения используют некие идеализации, применимость которых зависит от конкретной задачи. Среди этих понятий большую роль играют понятия: «материальная точка», «абсолютно твердое тело» и «сплошная среда».
Материальная точка – это тело, размерами которого можно пренебречь по сравнению с размерами других тел или по сравнению с расстояниями проходимыми телом.
Абсолютно твердое тело (далее просто твердое тело)– это система материальных точек, расстояния между которыми не меняются в процессе движения. Реальное тело можно считать абсолютно твердым, если в условиях данной задачи его деформацией можно пренебречь.
Сплошная среда — это модель для однородных систем с очень большим числом частиц.
Кинематика материальной точки
Кинематика – это раздел механики, изучающий движение тел, не интересуясь причинами, вызывающими это движение.
Описать движение материальной точки можно двумя способами: 1) написать уравнение зависимости радиус-вектора точки от времени (векторный способ)  или 2) три скалярных уравнения зависимости координат от времени (скалярный способ) x=f1(t); y=f2(t); z=f3(t). Эти уравнения называются кинематическими уравнениями движения материальной точки.
или 2) три скалярных уравнения зависимости координат от времени (скалярный способ) x=f1(t); y=f2(t); z=f3(t). Эти уравнения называются кинематическими уравнениями движения материальной точки.
Как описать движение материальной точки?
Траектория – это линия, описываемая материальной точкой в пространстве при её движении.
Пусть за некоторый промежуток времени Δt материальная точкапереместилась из точки 1 в точку 2. Тогда вектор, проведенный из начального положения материальной точки в конечное, называется вектором перемещения и обозначается 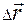 . Вектор перемещенияравен изменению радиус-вектора точкиза время
. Вектор перемещенияравен изменению радиус-вектора точкиза время  т.е.
т.е. 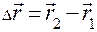 . Модуль вектора перемещения определяется по формуле
. Модуль вектора перемещения определяется по формуле
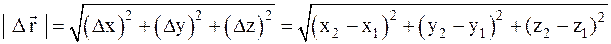 ,
,
где x1, y1, z1 –начальные координаты материальной точки;x2, y2, z2 –конечные координаты.
При бесконечно малом (элементарном) перемещении направление вектора перемещения 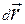 совпадает с направлением касательной к траектории в данной точке (в сторону движения точки).
совпадает с направлением касательной к траектории в данной точке (в сторону движения точки).
Путь  –это скалярная величина, равная сумме длин участков траектории.
–это скалярная величина, равная сумме длин участков траектории.
Векторная физическая величина, которая показывает как быстро и в каком направлении движется тело, называется линейной скоростью. В СИ единицей измерения скорости является метр на секунду (м/с).
Различают три разновидности линейной скорости движения материальной точки: 1) среднепутевую 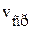 , 2) среднюю скорость перемещения
, 2) среднюю скорость перемещения  и 3) мгновенную скорость
и 3) мгновенную скорость  .
.
1). Если за время t материальная точка прошла путь S, то среднепутевая скорость:  .
.
2). Если за время  материальная точка переместилась на
материальная точка переместилась на 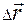 . Тогда средняя скорость перемещенияза время
. Тогда средняя скорость перемещенияза время  :
: 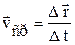 . Вектор средней скорости перемещения совпадает по направлению с вектором перемещения
. Вектор средней скорости перемещения совпадает по направлению с вектором перемещения 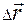 .
.
3). Чтобы определить скорость материальной точки в данный момент времени (мгновенную линейную скорость), необходимо устремить промежуток времени, за который определяется перемещение 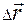 , к нулю.
, к нулю.
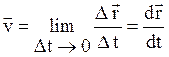 .
.
Вектор мгновенной линейной скоростиравен производной от радиус-вектора 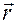 по времени и направлен по касательной к траектории в данной точке в сторону движения точки (как и
по времени и направлен по касательной к траектории в данной точке в сторону движения точки (как и 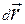 ).
).
Можно определить проекции вектора мгновенной на оси координат. При этом проекции вектора скорости на оси координат являются производными от соответствующих координат по времени: 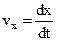 ;
;  ;
; 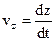 . Тогда модуль мгновенной скорости (так же как и модуль любого вектора) можно определить по формуле:
. Тогда модуль мгновенной скорости (так же как и модуль любого вектора) можно определить по формуле: 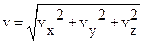 .
.
Введём понятие линейного ускорения – векторную величину, характеризующую быстроту изменения скорости. ВСИединицей измерения ускорения является метр на секунду в квадрате (м/с2).
Различают линейное ускорение 1) среднее  и 2) мгновенное
и 2) мгновенное 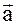 .
.
1). Если за время  скорость материальной точки изменилась на величину
скорость материальной точки изменилась на величину 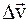 , то среднее ускорение за время
, то среднее ускорение за время  :
: 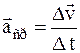 .
.
2). Мгновенное ускорение определяется как предел среднего при 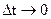 :
: 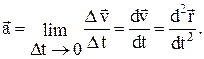 Мгновенное линейное ускорение равно первой производной от вектора мгновенной скорости
Мгновенное линейное ускорение равно первой производной от вектора мгновенной скорости 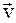 по времени или второй производной от радиус – вектора
по времени или второй производной от радиус – вектора 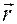 по времени.
по времени.
Так же как и для вектора мгновенной скорости проекции вектора ускорения на оси координат являются первыми производными от соответствующих скоростей и вторыми производными от соответствующих координат по времени: 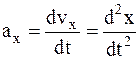 ,
, 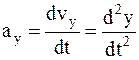 ,
,  . Модуль вектора ускорения:
. Модуль вектора ускорения: 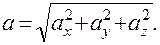
Движение с постоянным ускорением называется равноускоренным. Уравнения движения и скорости равноускоренного движения имеют вид: 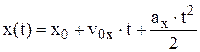 ,
, 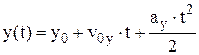 ,
, 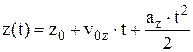 ,
, 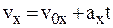 ,
, 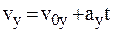 ,
, 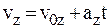 .
.
Частным случаем равноускоренного движения является движение в поле тяготения Земли. В этом случае (если ось ОZ перпендикулярна поверхности Земли, а оси OX и OY параллельны поверхности Земли) 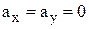 ,
, 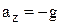 .
.
Плоское движение – это такое движение, при котором все участки траектории движения точки лежат в одной плоскости.
При криволинейном движении материальной точки ее скорость изменяется как по величине, так и по направлению. Вектор мгновенного ускорения 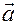 всегда направлен внутрь кривизны траектории и составляет некоторый угол с вектором мгновенной скорости
всегда направлен внутрь кривизны траектории и составляет некоторый угол с вектором мгновенной скорости 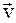 .
.
Для случая плоского криволинейного движения часто находят проекции вектора линейного ускорения не на оси x, y, а на два других взаимно перпендикулярных направления: касательное к траектории движения тела в данной точке и нормаль. Проекция ускорения на направление касательной – тангенциальная составляющая  , на нормаль – нормальная составляющая
, на нормаль – нормальная составляющая 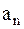 . В этом случае модуль вектора мгновенного ускорения может быть найден как
. В этом случае модуль вектора мгновенного ускорения может быть найден как 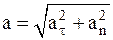 .
.
Тангенциальное ускорение определяется как первая производная от модуля мгновенной скорости по времени: 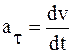 . Оно «отвечает» за изменение скорости по величине. Нормальное ускорение «отвечает» за изменение направления скорости. Его величина определяется по формуле:
. Оно «отвечает» за изменение скорости по величине. Нормальное ускорение «отвечает» за изменение направления скорости. Его величина определяется по формуле: 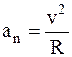 , где R – радиус кривизны траектории.
, где R – радиус кривизны траектории.
Дата добавления: 2015-04-15; просмотров: 221; Мы поможем в написании вашей работы!; Нарушение авторских прав |