КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
IV. Уравнение прямой, проходящей через данную точку в заданном направлении. Пучок прямых.
Глава 3. Аналитическая геометрия на плоскости и в пространстве
Прямая линия на плоскости
I. Уравнение прямой, проходящей через данную точку перпендикулярно заданному вектору
|
| y |
| x |
 (  ;  )
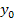M (x; 
|
| l |
| 0 |
(1) –уравнение прямой, проходящей через точку М0(x0;y0) и ⊥ .
Опр. Вектор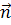 
, перпендикулярный данной прямой, называется нормальнымвектором прямой. Из (1) видно, что уравнение прямой – это уравнение первой степени (линейное) относительно текущих координат х и у.
Пример 1.1. Найти уравнение прямой, проходящей через точку М0(-1;2) и 
.
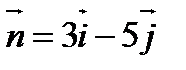II. Общее уравнение прямой.
Ax+By+C=0 (2) –общее уравнение прямой, где 
- нормальный вектор.
III. Каноническое уравнение прямой
| M0(x0;y0) |
|
| M(x;y) |
(3) – каноническое уравнение прямой (через точку М0(х0;y0)и параллельно вектору 
), 
– направляющий вектор прямой.
IV. Уравнение прямой, проходящей через данную точку в заданном направлении. Пучок прямых.
| α |
| x |
| y |
| α |
| y |
| x |
Опр. Углом α наклона прямой к оси Ox называется наименьший угол, на который надо повернуть против часовой стрелки ось Ox до совпадения её с прямой.
Рассмотрим на плоскости Oxy произвольную невертикальную прямую l.
| α |
| M0(x0;y0) |
| y |
| l |
| x |
| α |
|
|
Дано: m.M₀(x₀,y₀) є l
α – угол наклона прямой l к оси Ox
Требуется: составить уравнение прямой l
Воспользуемся уравнением (3).
В качестве направляющего вектора возьмем единичный вектор 
. Найдем m и n.
; 
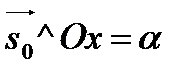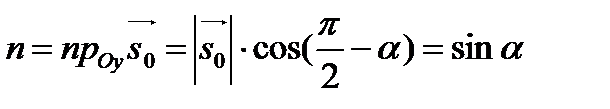
(3) 
Опр. Тангенс угла наклона прямой к оси Ox называется угловым коэффициентом прямой и обозначается k.
k=tgα – угловой коэффициент
Итак, 
(4) – уравнение прямой, проходящей через данную т.М0(х0;y0) в заданном направлении.
Замечание: Если прямая, проходящая через т. М0(х0;y0) параллельна оси Oy, т.е. α= 
, то k=tgα не определен. В этом случае уравнение может быть записано в виде 
.
Опр. Множество прямых, проходящих через некоторую точку плоскости называется пучком прямых, а их общая точка – центром пучка.
Если в уравнении (4) k считать переменной, то уравнение
(4) это уравнение пучка прямыхс центром в m. М0(х0;y0)(за исключением прямой ).
| M0(x0;y0) |
| y |
| x |
Дата добавления: 2015-04-15; просмотров: 133; Мы поможем в написании вашей работы!; Нарушение авторских прав |