КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ГИДРОЛИЗ СОЛЕЙ. Соли, образованные слабым основанием и сильной кислотой, сильным основанием и слабой кислотой, а также слабым основанием и слабой кислотой подвергаются
Соли, образованные слабым основанием и сильной кислотой, сильным основанием и слабой кислотой, а также слабым основанием и слабой кислотой подвергаются гидролизу в водных растворах. В результате гидролиза солей меняется рН среды. Гидролиз усиливается с повышением температуры и уменьшением концентрации солей.
Рассмотрим пример алгебраического выражения Кгидр. и h - степени гидролиза в растворе цианида калия.
KCN + H2O ↔ HCN + KOH
CN– + H2O ↔ HCN + OH–
;
KВОДЫ - 10–14 при 250 С, CKCN – концентрация соли, KHCN– константа диссоциации кислоты
Для соли типа CH3COONH4 (образованной слабым основанием и слабой кислотой)
; 
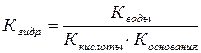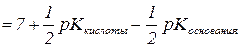
Соль слабого основания и сильной кислоты гидролизуется по катиону:
NH4Cl + H2O ↔ NH4OH + HCl
В ионном виде: NH4+ + H2O ↔ NH4OH + H+
Вычислить Кгидр., степень гидролиза и рН в растворах солей:
| № | соль | Концентрация, моль/дм3 или % | Кдисс. | рКдисс |
| 46. | (CH3COO)2Mg | 0,1 % | 1,74∙10-5 | 4,76 |
| 47. | Na2CO3 | 0,1 M | 4,8∙10-11 | 10,32 |
| 48. | NH4NO3 | 0,15 % | 1,76∙10-5 | 4,755 |
| 49. | (NH4)2CO3 | 0,03M | 1,76∙10-5 4,8∙10-11 | 4,755 10,32 |
| 50. | Na2S | 0,05M | 2,5∙10-15 | 12,60 |
| 51. | CuCl2 | 1% | 2,2∙10-20 | 19,66 |
| 52. | C6H5COONa | 1,5% | 6,3∙10-5 | 4,20 |
| 53. | Zn(NO3)2 | 0,15M | 1,2∙ 10-17 | 16,92 |
| 54. | (NH4)2S | 0,01M | 1,76∙10-5 2,5∙10-15 | 4,755 12,60 |
| 55. | CH3COOK | 0,2% | 1,74 ∙10-5 | 4,76 |
| 56. | Na3PO4 ( по 1 ступени) | 0,5% | 7,1∙ 10-3 | 2,15 |
| 57. | FeCl3 | 0,2M | 3,8∙ 10-38 | 37,42 |
| 58. | HCOOK | 0,01M | 1,8∙10-4 | 3,75 |
| 59. | Cr(NO3)3 | 0,5% | 6,3∙10-31 | 30,20 |
| 60. | MnBr2 | 0,3% | 2,05∙10-13 | 12,69 |
РАВНОВЕСИЕ В ГЕТЕРОГЕННЫХ СИСТЕМАХ
В насыщенном растворе малорастворимого электролита состава MmAn равновесное состояние можно схематически представить следующим образом.
MmAn ↔ mMn+ + nAm–
Концентрационная константа растворимости
Kc = [ Mn+]m ×[ Am–]n = ПР(MmAn),
Например, для PbCl2: Kc = [Pb2+]×[Cl–]2= ПР(PbCl2)
Связь растворимости выраженной в моль/дм3 с ПР, при малом значении ионной силы, описывается уравнением:
В присутствии сильного электролита, не имеющего одноименных ионов с малорастворимой солью, необходимо вычислить ионную силу раствора и рассчитать или взять из таблицы коэффициенты активности ионов, входящих в состав малорастворимой соли
В присутствии избытка электролита с одноименным ионом, например с ионом А–:
Пример 3: Образуется ли осадок AgCl, если к раствору, содержащему 3,4 г AgNO3 в 1 дм3 прилить равный объем раствора СNaCl = 0,02 моль/дм3
Решение: M(AgNO3) = 169,87 г/моль [AgNO3] = 3,4/169,87 = 0,02 моль/дм3
[Ag+] =[AgNO3] = 0,02 моль/дм3
После смешения равных объемов растворов, концентрация ионов [Ag+] и [Cl-] уменьшится в 2 раза
[Ag+] × [Cl-] = 0,01×0,01 = 10–4; ПР(AgCl) = 1,8×10–10, Þ осадок образуется.
Пример 4: Вычислить рН, при котором практически полностью осаждается Mg(OH)2, если ПР Mg(OH)2 = 2×10–11
Решение: ПР Mg(OH)2=[Mg2+][OH–]2, практической полнотой осаждения принято считать, если концентрация осаждаемого иона не превышает 10–5¸10–6 моль/ дм3
; 
рОН = −lg [OH–]= −lg 4,5∙ 10−3 = 2,35 ; pH = 14 − 2,35 = 11,65.
Пример 5: Смешаны равные объемы 0,001 М BaCl2 и 1,5×10-3М Na2SO4. Вычислить [Ba2+] в растворе, если ПР BaSO4= 1,1×10−10, и как измениться растворимость BaSO4 в этой смеси по сравнению с растворимостью в воде.
Решение: После смешивания растворов концентрации хлорида бария и сульфата натрия уменьшатся вдвое: 
После завершения реакции: BaCl2 + Na2SO4→ BaSO4 ↓ + 2NaCl
[SO42-] = (7,5 – 5)×10-4= 2,5×10-4 M 
Растворимость BaSO4 в воде: 
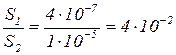Þ Растворимость в электролите, имеющем одноименный ион, уменьшилась.
Вычислить растворимость в моль/дм3 и г/дм3, если известно произведение растворимости соли:
| № | соль | ПР | № | соль | ПР |
| 61. 1 | PbBr2 | 3,9´10-5 | 66. 1 | Pb3(AsO4)2 | 4,1´10-39 |
| 62. 1 | BiI3 | 8,1´10-19 | 67. 1 | Ag3PO4 | 1,3´10-20 |
| 63. 1 | Ag2SO4 | 1,6´10-5 | 68. 1 | Ag2SO4 | 1,5´10-14 |
| 64. 1 | PbI2 | 7,2´10-9 | 69. 1 | La(IO3)3 | 6,2´10-12 |
| 65. 1 | Sr(IO3)2 | 3,3´10-7 | 70. 1 | Ag2CrO4 | 1,1´10-12 |
Зная произведение растворимости, вычислить рН начала и конца осаждения гидроксидов и их растворимость в г/дм3:
| № | гидроксид | ПР | № | гидроксид | ПР |
| 71. 1 | Fe(OH)2 | 3,0´10-16 | 76. 1 | Al(OH)3 | 3,2´10-34 |
| 72. 1 | Cu(OH)2 | 2,2´10-20 | 77. 1 | Zn(OH)2 | 1,2´10-17 |
| 73. 1 | Mn(OH)2 | 4,0´10-14 | 78. 1 | Sn(OH)2 | 6,3´10-27 |
| 74. 1 | Fe(OH)3 | 3,8´10-38 | 79. 1 | Cr(OH)3 | 6,3∙´10-31 |
| 75. 1 | Co(OH)2 | 2.0´10-16 | 80. 1 | Pb(OH)2 | 5,0´10-16 |
По величине ПР вычислить растворимость малорастворимого электролита с учетом коэффициентов активности ионов. (Концентрация дана в моль/ дм3 или в массовых долях):
| Малорастворимое вещество | ПР | Сильный электролит | концентрация | |
| 76. | CuCNS | 4,8´10-15 | CuSO4 | 0,5M |
| 77. | Mn(OH)3 | 1,0´10-36 | NaOH | 0,3M |
| 78. | Pb3(PO3)2 | 7,8´10-43 | Na3PO4 | 0,2M |
| 79. | CdCO3 | 1.0´10-12 | CdCl2 | 0,1M |
| 80. | AgCN | 1,4´10-16 | AgNO3 | 0,1M |
| 81. | PbS | 2,5´10-27 | Pb(NO3)2 | 0,1M |
| 82. | AgCl | 1,78´∙10-11 | NaCl | 0,05M |
| 83. | BiPO4 | 1,3´10-23 | K3PO4 | 0,05M |
| 84. | Cu(OH)2 | 2,2´10-20 | CuSO4 | 0,04M |
| 85. | PbCrO4 | 1,8´10-14 | K2CrO4 | 0,03M |
| 86. | Ca3(PO4)2 | 2,0´10-29 | Ca(NO3)2 | 2,5% |
| 87. | CuS | 6,3´10-36 | CuSO4 | 2% |
| 88. | BaSO4 | 1,1´10-10 | Na2SO4 | 0,02M |
| 89. | AgBr | 5,3´10-13 | KBr | 0,02M |
| 90. | Co(OH)3 | 4,0´10-45 | KOH | 2% |
| 91. | Fe(OH)2 | 3,0´10-16 | NaOH | 1,5% |
| 92. | Co(OH)2 | 2,0´10-16 | CoCl2 | 0,01M |
| 93. | MnS | 2,5´10-11 | Mn(NO3)2 | 0,9% |
| 94. | Mg(OH)2 | 7,1´10-12 | MgCl2 | 0,3% |
| 95. | Ag3PO4 | 1,3´10-20 | AgNO3 | 0,2% |
РАВНОВЕСИЯ В РАСТВОРАХ КОМПЛЕКСНЫХ СОЕДИНЕНИЙ
Равновесия в растворах комплексных соединений характеризуется константой устойчивости комплекса: 
Отношение общей концентрации соли металла к равновесной концентрации его ионов - есть функция закомплексованности Ф
; 
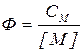Доля образующегося комплекса вычисляется следующим образом:
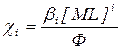
Если лиганд является анионом слабой кислоты или основания, то функция закомплексованности зависит от рН растворителя, а равновесная концентрация лиганда: [L-m] = C(HmL)´αm ;
где C(HmL) – общая концентрация кислоты, αm – доля аниона кислоты
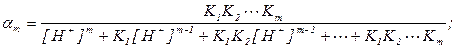
K1, K2 - Km – константы диссоциации кислоты
В этом случае уместно пользоваться значением условной константы устойчивости βn'
Пример 6: Рассчитайте равновесную концентрацию ионов серебра в 0,01 М растворе AgNO3 в присутствии 2 М раствора аммиака.
Решение: В растворе устанавливается равновесие:
;
;
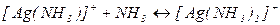
101. Вычислить равновесную концентрацию ионов серебра в растворе, содержащем 10-3 М нитрата серебра и 0,102 М цианида калия, принимая во внимание, что в этих условиях существует в основном комплекс Ag (CN)-2 .
102. К 100 см3 1×10-3 М раствора нитрата ртути (2) добавлено 100 см3 0,64 М раствора роданида аммония. Вычислить равновесную концентрацию ионов ртути (2), учитывая, что в указанных условиях преобладает комплекс Hg(SCN)42-.
103. К 25 см3 2×10-3 М раствора хлорида ртути (2) добавлено 0,7305 г хлорида натрия. Вычислить равновесную концентрацию Hg2+, закомплексованность и долю комплекса HgCL42-.
104. Вычислить закомплексованность и равновесную концентрацию Ag+ в растворе, содержащем 1∙10-3 М нитрата серебра и 0,022 М аммиака. Ионная сила равна 0,5.
105. Ионы меди (2) образуют с аммиаком комплекс состава Cu(NH3)n2+, (n = 1-4). Вычислить концентрацию комплекса Cu(NH3)22+ в растворе, в котором общая концентрация ионов меди равна 0,001 М, а равновесная концентрация аммиака составляет 0,01 моль/дм3. Ионная сила равна 1.
106. В растворе возможно существование смеси комплексов никеля состава Ni(NH3)n2+, (n=1-4). Найти закомплексованность и концентрацию комплекса Ni(NH3)42+ при общей концентрации ионов никеля 1×10-4 М, если равновесная концентрация аммиака составляет 10-3 моль/дм3. Ионная сила раствора равна 2.
107. Вычислить закомплексованность и равновесную концентрацию Co2+в 1×10-2 М растворе хлорида кобальта, содержащем 1,04 М аммиак, при ионной силе равной 1.
108. Найти концентрацию комплексных анионов Cu(S2O3)35- при общей концентрации ионов меди (1) 1×10-3 М, если равновесная концентрация S2O32- равна 1×10-2 М, а ионная сила 0,1.
109. Рассчитайте равновесную концентрацию Ag(NH3)2+ в 0,01 М растворе нитрата серебра в присутствии 2 М аммиака.
110. Рассчитайте равновесную концентрацию иона кобальта (2) в 0,100 М растворе хлорида кобальта (2), содержащего 2 М аммиака.
111. Рассчитайте равновесную концентрацию Cu (NH3)2+ в 1·10-2 М растворе сульфата меди (2) в присутствии 1 М аммиака.
112. Рассчитайте равновесную концентрацию FeF2+ в 0,100 М растворе хлорида железа (3) в присутствии 1 М фторида аммония.
113. Рассчитайте равновесную концентрацию ионов меди (1) в растворе, образовавшемся при прибавлении избытка 2М цианида калия к 1·10-2 М раствору меди (2).
114. Рассчитайте равновесную концентрацию ионов ртути (2) в 1·10-2 М растворе нитрата ртути (2) в присутствии 1 М йодида калия.
115. Рассчитайте степень образования HgI3– и HgI42- в растворе с равновесной концентрацией йодид-иона 0,100 М.
РАВНОВЕСИЯ В ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ СИСТЕМАХ
СТАНДАРТНЫЙ ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ И
КОНСТАНТА РАВНОВЕСИЯ РЕАКЦИИ ОКИСЛЕНИЯ ВОССТАНОВЛЕНИЯ
Количественной характеристикой окислительно - восстановительной системы является окислительно-восстановительный потенциал, величина которого вычисляется по уравнению Нернста:
Если в окислительно-восстановительной полуреакции участвуют ионы водорода, то в уравнение Нернста входит концентрация ионов водорода:
Ox + ne + mH+ ↔ Red ;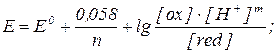 
Глубина протекания реакций определяется константой равновесия:
Пример 7: Рассчитайте константу равновесия реакции между арсенатом натрия и иодидом калия при рН=0.
Решение:
H3AsO4 + 3I– + 2H+ ↔ H3AsO3 + H2O + I3– ; I3– + 2e ↔ 3I– ;
E0 I3– / 3I– = + 0,535 B; E0 H3AsO4 / H3AsO3 = + 0.559 B;
Для полной реакции: H3AsO4 + 3I– + 2H+ ↔ H3AsO3 + H2O + I3– ;
ΔE0 = 0,559-0,535 = + 0,024 B
Положительная разность потенциалов указывает на протекание реакции слева направо
Kр = 100,83;
следовательно, глубина протекания реакции невелика, поскольку разность потенциалов при рН = 0 небольшая.
Расчет стандартных потенциалов полуреакции
Если стандартные потенциалы полуреакций:
Ox1 + ne ↔ Red1 и Ox2 + me ↔ Red2
известны (Е01 и Е02), то стандартный потенциал полуреакции:
Ox1 + (m+n)e ↔Red1
можно рассчитать по формуле: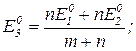 
Пример 8: Рассчитайте стандартный потенциал полуреакции
H3SO3 + 6e + 6H+↔ H2S + 3H2O
E0 S/H2S = + 0,14 В; E0 H2SO3/S = + 0,45 В
Решение: Сочетание двух полуреакций
S + 2H+ + 2e ↔ H2S и H3SO3+ 4H+ + 4e↔3H2O + S,
для которых известны стандартные потенциалы, дает полуреакцию
H3SO3 + 6e + 6H+↔ H2S + 3H2O
Стандартный потенциал, которой:
Для расчета стандартного потенциала полуреакций, получаемых сочетанием полуреакций окисления или восстановления, и реакции осаждения используются формулы:
если окисленная форма представляет cобой малорастворимое соединение:
если восстановленная форма представляет собой малорастворимое соединение:
Для расчета стандартного потенциала полуреакции, получаемой сочетанием полуреакций окисления или восстановления и реакции комплексообразования используются формулы:
Если окисленная форма связана в комплекс: 
Если восстановленная форма связана в комплекс: 
Если обе формы связаны в комплекс: 
Расчет стандартного потенциала полуреакции, получаемой сочетанием полуреакции окисления или восстановления и реакции протонирования.
Если протонируется окисленная форма: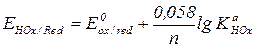 
Если протонируется восстановленная форма: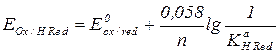 
Если протонируются обе формы: 
Рассчитайте стандартный потенциал полуреакции (1) исходя из величины Е0 полуреакции (2):
| № | Реакция 1 | Реакция 2 | Е0, В |
| 116. | AgI + ē ↔Ag + I– | Ag+ + ē ↔ Ag | 0,799 |
| 117. | Al3+ + 3ē↔ Al | AlF63– + 3ē ↔ Al + 6F– | -2,07 |
| 118. | Cu2+ + Cl– + ē ↔ CuCl | Cu2+ + ē ↔ Cu+ | 0,52 |
| 119. | IO3– + 6H++ ē ↔ I– + 3H2O | IO3– + 4H+ + 4ē ↔IO– +2H2O IO– + 2H +2ē ↔ I– + H2O | 0,97 1,31 |
| 120. | 2HNO2 + 6H+ + 6ē↔ N2 + 4H2O | 2NO2– + 8H+ + 6ē ↔ N2 + 4H2O | 1,52 |
| 121. | Ag2CrO4 + 2ē ↔ 2Ag + CrO42– | Ag+ + ē ↔ Ag | 0,799 |
| 122. | Cd2+ + 2ē ↔ Cd | Cd(NH3)2+ + 2ē ↔ Cd + 4NH3 | - 0,61 |
| 123. | Fe(CN)63– + ē ↔ Fe(CN)64– | Fe3+ + ē ↔ Fe2+ | 0,77 |
| 124. | Ag2S + 2ē ↔ 2Ag + S2– | Ag+ + ē ↔ Ag | 0,799 |
| 125. | Al3+ + 3ē ↔ Al | Al(OH)4– + 3ē ↔ Al + 4OH– | - 2,31 |
| 126. | H2AsO4– + 3H++2 ē ↔ HАsO2 + 2H2O | H3AsO4 + 2H+ + 2ē ↔ HАsO2 + 2H2O | 0,56 |
| 127. | Bi(OH)3 +3ē ↔ Bi + 3OH– | Bi3+ +3 ē ↔ Bi | 0,215 |
| 128. | Co3+ + ē ↔ Co2+ | Co(NH3)63+ + ē ↔ Co(NH3)62+ | 0,1 |
| 129. | VO22+ + 4H++3ē ↔ V3+ + 2H O | VO2+ + 2H+ + ē ↔ V3+ + H2O VO2+ +2H+ + ē ↔ VO2+ + H2O | 0,34 1,00 |
| 130. | SO42– + 10H+ + 8 ē ↔ H2S + 4H2O | H2SO3 + 6H+ + 6 ē ↔ H2S + 3H2O SO42– + 4H+ + 2ē ↔ H2SO3 + H2O | 0,35 0,17 |
Вычислить константы равновесия для реакций, протекающих между следующими реагентами:
131. I2 + Na2S2O3 →
132. FeSO4 + KMnO4 + H2SO4→
133. Na3AsO4 + KI + HCl →
134. FeSO4 + Ce(SO4)2 + H+→
135. NH4VO3 + FeSO4 + H+→
136. Na2Cr2O7 + KI + H+ →
137. FeCl3 + SnCl2→
138. Cl2 + HBr →
139. KMnO4– + HCl→
140. FeCl3 + H2→
141. FeCl3 + KI + H+ →
142. K2Cr2O7 + FeSO4 + H2SO4→
143. HI + Br2→
144. H2SO3 + I2 + H2O→
145. SnCl2 + Br2→
ЧУВСТВИТЕЛЬНОСТЬ АНАЛИТИЧЕСКИХ РЕАКЦИЙ
Количественно чувствительность реакции характеризуется следующими показателями: открываемый минимум, предельная (минимальная) концентрация и минимальный объем предельно разбавленного раствора.
Открываемый минимум (m) – наименьшее количество вещества, которое при определенных условиях можно открыть действием данного реагента: выражается в микрограммах: 1 мкг = 10-6 г.
Предельная концентрация (Спред.) – отношение единицы массы (1г) определяемого иона к массе наибольшего количества растворителя; выражается в г/ см3. Величина, обратная предельной концентрации – предельное разбавление
Пример 9: Вычислить предельную концентрацию и предельное разбавление раствора соли Pb2+, если открываемый минимум Pb2+ 0,15 мкг, а минимальный объем раствора, необходимый для открытия свинца в виде хромата, равен 0,03 см3.
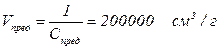
146. Вычислить предельное разбавление и минимальную концентрацию, если открываемый минимум соли натрия, определяемой в виде цинк-уранил ацетата, составляет 12,5 мкг, а минимальный объем 0,05 см3.
147. Микрокристаллоскопическая реакция на ион Mg2+ в виде соли MgNH4PO4 удается с предельно разбавленным раствором, содержащим 1,2 10-5 г/ см3 Mg2+. Минимальный объем 0,001 см3 Найти открываемый минимум.
148. Реакция ионов серебра с иодидом калия удается при разбавлении 75000 см3/г. Открываемый минимум равен 0,13 мкг. Каков минимальный объем исследуемого раствора.
149. Реакция на SO42- c хлоридом кальция удается при наличии 0,21 мкг определяемого иона в объеме 0,02 см3. При каком разбавлении возможна эта реакция.
150. Открываемый минимум ионов Zn2+ в виде соли Zn[Hg(CNS)4] равен 0,1 мкг. Минимальный объем исследуемого раствора 0,005 см3. Найти предельное разбавление.
151. Вычислить минимальный объем соли Cu2+ в виде соли Cu[Fe(CN)6] открываемый минимум равен 0,02 мкг, а предельное разбавление раствора равно 2500000 см3/г.
152. Капельная реакция на никель с диметилглиоксимом позволяет обнаружить 0,0625 мкг никеля в капле объемом 0,05 см3. Вычислить предельное разбавление.
153. Минимальный объем раствора, необходимый для открытия NH4+ реактивом Несслера, равен 5 см3. Вычислить открываемый минимум, если предельное разбавление ионов NH4+ в растворе равно 20 000 000 см3/г.
154. Ион PO43- определяется из 0,005 М раствора фосфата натрия действием ацетата свинца в объеме 0,003 см3. Рассчитать открываемый минимум иона PO43-.
155. В дм3 воды содержится 0,5 г Cu2+. Открываемый минимум иона Cu2+ с гидроксидом аммония 0,2 мкг. Рассчитать минимальный объем раствора, содержащего открываемый минимум определяемого иона.
156. Открываемый минимум ионов Pb2= c KI в уксуснокислой среде 0,07 мкг в объеме 0,05 см3. Вычислить предельную концентрацию и предельное разбавление исследуемого раствора.
157. Ион Ag+ с хроматом калия определяется из объема 0,001 см3 0,02 М раствора нитрата серебра. Найти предельное разбавление и открываемый минимум исследуемого раствора.
158. Открываемый минимум реакции иона калия с кобальтинитритом натрия составляет 0,12 мкг. Предельная концентрация раствора равна 1 : 8 000 г/см3. вычислить минимальный объем.
159. Чему равен открываемый минимум реакции обнаружения иона кальция в виде оксалата, если она удается с 0,001 см3 0,001 М раствора хлорида кальция.
160. Вычислить Vmin для реакции иона CrO42- c карбазидом, если открываемый минимум этой реакции 0,25 мкг, а предельная концентрация 1/2·10-5 г/ см3.
Дата добавления: 2015-04-15; просмотров: 222; Мы поможем в написании вашей работы!; Нарушение авторских прав |