КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Угловая скорость и угловое ускорение.
Пройденный путь S, перемещение dr, скорость v, тангенциальное и нормальное ускорение at, и an, представляют собой линейные величины.
Для описания криволинейного движения наряду снимиможно пользоваться, так называемыми, угловыми величинами.
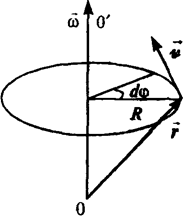Рассмотрим важный и часто встречаемый случай движения по окружности. В этом случае наряду с длиной дуги окружности движение можно характеризовать утлом поворота 
вокруг оси вращения.
Определение 1.
Величину 
(1) называют угловой скоростью. Угловая скорость представляет собой вектор, направленный по оси вращения тела.
И если угол поворота φ является скаляром, то бесконечно малый поворот dφ — векторная величина, направление которой определяется по правилу правой руки, или буравчика, и связано с осью вращения.
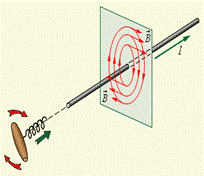
// Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.//
Если вращение является равномерным, то ω = constи имеет место поворот на равные углы вокруг оси вращения за равные времена.
//Фильм «Круговое движение»_9 мин.//
Определение 2.
Время, за которое точка на окружности совершает полный оборот, т.е. поворачивается на угол 2π,называется периодом движения Т.
Определение 3.
Угловой частотой называется величина, определяемая выражением вида: 
. (2)
Выражение (2) можно представить как результат интегрирования формулы (1). Действительно, 
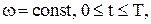. При 
и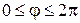 
получаем, что 
.
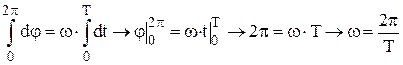Определение 4.
Дата добавления: 2015-04-15; просмотров: 205; Мы поможем в написании вашей работы!; Нарушение авторских прав |