Распределение терминов в категорических суждениях.

Все рассмотренные выше виды категорических суждений имеют в качестве субъекта и предиката понятия (или термины), которые в каждом отдельном случае могут быть либо распределёнными, либо нераспределенными.

Распределённым термином (или понятием) называется такой термин, которые в данном суждении взят во всём объёме. Если же термин в данном суждении взят не во всём объёме, а лишь частично, то такой термин называется нераспределённым.

Рассмотрим все виды суждения с точки зрения распределённости в них понятий, стоящих на месте субъекта и предиката.
В общеутвердительных суждениях (А), понятия, которые находятся на месте субъекта, должны быть всегда распределёнными, то есть взяты во всём объёме. Если же это требование не будет выполнено (термин не будет распределён), то суждение перестаёт быть общеутвердительным, как правило, является нераспределенным. Лишь тогда, когда объём предиката равен объёму субъекта, термин на месте предиката является также распределённым.

Рассмотрим на примерах оба этих случая распределённости терминов в общеутвердительных суждениях.

1-ый случай. Возьмём суждение «Все студенты должны сдавать экзамены». Термин, стоящий на месте субъекта («все студенты» у нас распределён); термин же, стоящий на месте предиката («должны сдавать экзамены) нераспределён и участвует по своему объёму лишь частично: все знают, что сдавать экзамены должны не только студенты, но и школьники; дипломированные студенты, если они проходят курс обучения; космонавты, автомобилисты, и пр. пр.. Подавляющее большинство терминов, стоящих на месте предиката в общеутвердительных суждениях, находятся в отношении подчинения, где подчиняющим является предикат, подчинённый субъект. Графически эти отношения могут быть изображены кругами Эйлера.

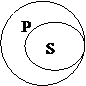
2-ой случай, когда в общеутвердительных суждениях понятия на месте предиката являются распределёнными. Например: «Все квадраты – прямоугольники с равными сторонами», «Киев – столица Украины» и т. п.. В этих суждениях объёмы понятий, стоящих на месте предиката и субъекта равны, т.е. они распределены. Графическое изображение тождества двух понятий будет таким:

В общеотрицательных суждениях (Е) термины как на месте субъекта, так предиката всегда распределены. Это связано с тем, что объект понятия, стоящего на месте предиката, полностью исключает из субъекта понятия, стоящего на месте субъекта. Например: «Ни одна рыба (S) не является теплокровным животным (P)»; «Ни один человек (S) не имеет крыльев (P)» и так далее. Графически термины при этом изображаются так, что их объёмы несовместимы.

В частноутвердительных суждениях (I) термин на месте субъекта всегда нераспределён. Термин же на месте предиката, как правило является нераспространённым, но бывает исключение, когда термин на месте предиката в частноутвердительных суждениях является распределёнными. Рассмотрим оба случая.
1-ый случай, как правило термины и на месте субъекта, и на месте предиката являются нераспределенными. Например: «Некоторые студенты (S) изучают высшую математику (P)», или «Некоторые государства (S) придерживаются политики нейтралитета (P)» и так далее. Графически термины в таких суждениях находятся в отношении частичного совпадения.

2-ой случай, когда на месте предиката стоит распределённый термин. Например: «Некоторые позвоночные (S) являются млекопитающими (P)», «Некоторые виды растений(S) занесены в Красную книгу (P)» и так далее. В этих примерах понятия на месте субъекта нераспределёнными, а на месте предиката распределёнными. Графически это выражено отношением подчинения, где предикат полностью входит в объём понятия субъекта, но его не исчерпывает.

В частоотрицательных суждениях (О) термин на месте субъекта всегда нераспределён, а термин на месте предиката всегда распределён. Это связано с тем, что в таких суждениях весь объём предиката исключается из части объёма субъекта. Например: «Некоторые животные (S) не являются хищниками (P)», «Некоторые служащие (S) не являются руководителями (P)», и так далее. Во всех примерах такого типа предикат полностью исключается из части объёма субъекта. Графически это сходно с отношением перекрещивающихся понятий, но это касается той части объёма субъекта, которая не входит в объём предиката.

Бывают примеры, когда объём предиката не выходит за рамки объёма субъекта, но всё равно объём предиката полностью отрицается в части объёма субъекта. Поэтому во всех частоотрицательных суждениях понятия на месте субъекта всегда нераспределены, а понятия на месте предиката всегда распределены. Графически это сходно с отношением между понятиями типа подчинения, но предикат полностью отрицается в части объёма субъекта.

Проьблема истинности

Таблица истинности – таблица, с помощью которой устанавливается значение истинности сложного суждения в зависимости от значения истинности простых суждений, входящих в его состав. Каждое из сложных суждений имеет свою таблицу истинности. В классической логике сводные данные для конъюнкции, дизъюнкции, импликации и эквиваленции имеют следующий вид (табл. 3.1.):

Таблица 3.1. Таблица значений истинности:

буква «и» соответствует значению «истинно», буква «л» – значению «ложно»

Выделяют следующие правила соотношения истинности и ложности суждений:

1. Из истинности общего, подчиняющего суждения следует истинность подчиненного частного суждения.

2. Из ложности общего суждения не вытекает ни истинность, ни ложность частного суждения, – оно остается неопределенным.

3. Ложность частного суждения обусловливает ложность подчиняющего общего суждения, но истинность частного оставляет общее суждение неопределенным.