ИНТУИЦИОНИСТСКАЯ ЛОГИКА

Интуиционистская логика построена в связи с развитием ин­туиционистской математики. Интуиционистская школа основана в 1907 г. голландским математиком и логиком Л. Брауэром (1881—1966)³⁵, но некоторые ее идеи выдвигались и ранее.

Интуиционизм — философское направление в математике и логике, отказывающееся от использования абстракции актуаль­ной бесконечности, отвергающее логику как науку, предшест­вующую математике, и рассматривающее интуитивную ясность и убедительность («интуицию») как последнюю основу матема­тики и логики. Интуиционисты свою интуиционистскую матема­тику строят с помощью финитных (конечных) средств на основе системы натуральных чисел, которая считается известной из интуиции. Интуиционизм включает в себя две стороны — фило­софскую и математическую.

Математическое содержание интуиционизма изложено в ряде работ математиков. Ведущие представители отечественной шко­лы конструктивной математики отмечают положительное значе­ние некоторых математических идей интуиционистов.

В целом конструктивная математика существевно отличается от интуиционистской. Советский математик-конструктивист А. А. Марков (1903—1979) пишет о том, что конструктивное направление имеет точки соприкосновения с так называемой интуиционистской математикой. Конструктивисты сходятся с интуиционистами в понимании дизъюнкции и в силу этого призна­ют правильной данную Брауэром критику закона исключенного третьего. Вместе с тем конструктивисты считают неприемлемы­ми методологические основы интуиционизма.

В этом высказывании ясно разделены две стороны интуици­онизма — математическая и философская. Если первая сторона имеет рациональную часть (в этой связи предпочтительнее гово­рить об интуиционистской математике или интуиционистской логике, а не об интуиционизме), то вторая сторона интуициониз­ма (его методологические, идеалистические, философские осно­вы) совершенно неприемлема.

Брауэр считал, что чистая математика представляет собой свободное творение разума и не имеет никакого отношения к опытным фактам. У интуиционистов единственным источни­ком математики оказывается интуиция, а критерием приемлемо­сти математических понятий и выводов является «интуитивная ясность». Но интуиционист Гейтинг вынужден признаться в том, что понятие интуитивной ясности в математике само не является интуитивно ясным; можно даже построить нисходящую шкалу степеней очевидности.

Основой происхождения математики в конечном итоге является не какая-то «интуитивная ясность» — продукт сознания человека, а отражение пространственных форм и количественных отношений действительного мира. Гейтинг, как и Брауэр, в гносеологии тоже субъективный идеалист. Он утверждает, что для математической мысли характерно, что она не выражает истину о внешнем мире, а связана исключительно с умственными построениями³⁶.

Еще в 1936 г. советский математик А. Н. Колмогоров под­верг критике субъективно-идеалистические основы интуициониз­ма, заявив, что невозможно согласиться с интуиционистами, когда они говорят, что математические объекты являются про­дуктом конструктивной деятельности нашего духа, ибо матема­тические объекты являются абстракциями реально существую­щих форм независимой от нашего духа действительности. Интуиционисты не признают человеческую практику и опыт источни­ком формирования математических понятий, методов математи­ческих построений и методов доказательств.

Особенности интуиционистской логики вытекают из характер­ных признаков интуиционистской математики.

В современной классической математике часто прибегают к косвенным доказательствам. Но их почти невозможно ввести в интуиционистской математике и логике, так как там не призна­ются закон исключенного третьего и закон 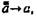которые уча­ствуют в косвенных доказательствах.

Закон исключенного третьего для бесконечных множеств в ин­туиционистской логике не проходит потому, что 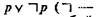знак отрицания) требует общего метода для решения любой проблемы или, более явно, общего метода, который по произ­вольному высказыванию р позволил бы получать либо доказате­льство р, либо доказательство отрицания р. Гейтинг считает, что так как интуиционисты не располагают таким методом, то они и не вправе утверждать принцип исключенного третьего. Пока­жем это на таком примере. Возьмем утверждение: «Всякое целое число, большее единицы, либо простое, либо сумма двух про­стых, либо сумма трех простых». Неизвестно, так это или нет, хотя в рассмотренных случаях, которых конечное число, это так. Существует ли число, которое не удовлетворяет этому требова­нию? Мы не можем указать такое число и не можем вывести противоречие из допущения его существования.»

Эта знаменитая проблема Гольдбаха (X. Гольдбах — мате­матик) была поставлена им в 1742 г. и не поддавалась решению около 200 лет. Гольдбах высказал предположение, что всякое целое число, большее или равное шести, может быть представ­лено в виде суммы трех простых чисел. Для нечетных чисел она была положительно решена только в 1937 г. советским матема­тиком — академиком И. М. Виноградовым; все достаточно большие нечетные числа представимы в виде суммы трех про­стых чисел. Это одно из крупнейших достижений современной математики. Но закон непротиворечия представители как инту­иционистской, так и конструктивной логик считают неограничен­но применимым.

Брауэр первый наметил контуры новой логики. Идеи Брауэра формализовал Гейтинг, в 1930 г. построивший интуиционистское исчисление предложений с использованием импликации, конъюн­кции, дизъюнкции и отрицания на основе 11 аксиом и двух правил вывода — модуса поненс (modus ponens) и правила под­становки. Гейтинг утверждает, что, хотя основные различия меж­ду классической и интуиционистской логиками касаются свойств отрицания, эти логики не совсем совпадают и в формулах без отрицания. Гейтинг отличает математическое отрицание от фак­тического: первое выражается в форме конструктивного постро­ения (выполнения) определенного действия, а второе говорит о невыполнении действия (а «невыполнение» чего-либо не являет­ся конструктивным действием). Интуиционистская логика имеет дело только с математическими суждениями и лишь с математическим отрицанием, которое определяется через понятие проти­воречия, а понятие противоречия интуиционисты считают перво­начальным, выражающимся или приводящимся в форме 1 = 2, Фактическое отрицание не связано с понятием противоречия.

Проблемами интуиционистской логики в нашей стране зани­маются К. Н. Суханов, М. И. Панов, А. Л, Никифоров и др.