
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПОЛОЖИТЕЛЬНЫЕ ЛОГИКИ
Положительные логики — это логики, построенные без операции отрицания. Их можно разделить на два вида: 1) положительные логики в широком смысле слова, или квазипозитивные логики. Они построены без операции отрицания, но отрицание может быть выражено средствами этой логической системы; 2) положительные логики в узком смысле слова, т. е. логики, построенные без операции отрицания, причем отрицание не может быть выражено средствами этой системы. Можно предложить классификацию и по другому основанию: числу логических операций, с помощью которых построена положительная логика. Квазипозитивными логиками, построенными на одной операции, являются логика, построенная на операции «штрих Шеффера» (антиконъюнкции), и логика, основанная на операции антидизъюнкции. Квазипозитивная логика, построенная на операции антидизъюнкции, которая соответствует сложному союзу «ни..., ни...» и обозначается 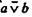 («ни а, ни b»), таблично определена так (табл. 24):
(«ни а, ни b»), таблично определена так (табл. 24):
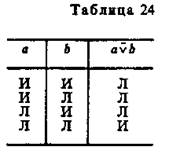
Ряд квазипозитивных логик основан на двух операциях. Положительными логиками в узком смысле, основанными на одной операции, являются импликативная логика, основанная на операции импликации, и логика, построенная на операции эквиваленции. Ряд положительных логик основан на двух операциях: а) на импликации и конъюнкции; б) на дизъюнкции и конъюнкции; в) на импликации и дизъюнкции.
Положительная логика (в узком смысле) является подсистемой (частичной системой) более сильных логик — интуиционистской и классической. Все утверждения положительных логик имеют силу как в интуиционистской логике, так и в классической логике. Внутри самих положительных логик также имеются различные по силе системы. Так, импликативная логика, включающая две аксиомы, слабее, чем положительная логика, включающая, кроме этих двух, аксиомы, характеризующие конъюнкцию и дизъюнкцию. Аксиоматическое построение подтверждает это соотношение: самой сильной является классическая, слабее — интуиционистская, еще слабее — положительная логика.
Общеемежду положительной логикой в широком смысле и положительной логикой в узком смысле в том, что среди логических констант этих систем нет операции отрицания.
Отличияэтих систем следующие: 1) в квазипозитивных логиках операция отрицания выразима средствами этой логики, а в положительных логиках в узком смысле операция отрицания не выразима; 2) квазипозитивные логики являются моделями классической логики, т. е. они эквивалентны классической логике высказываний. Положительные логики в узком смысле не эквивалентны классической логике, а являются ее подсистемой (частичной системой), а следовательно, слабее классической логики высказываний.
Роль положительных логик в искусственных языках весьма значительна, особенно конструктивной логики А. А. Маркова, которая строится на иерархии языков. В алфавите языка Я\ нет
отрицания, и в нем нельзя выразить отрицание, ибо нет импликации. Марковым был построен язык Я1 ,который хотя и узок, но приспособлен для описания работы нормальных алгоритмов. Этот язык пригоден для выражения некоторых отношений между словами, встречающимися в чистой семиотике и в теории алгоритмов. С помощью языка Я\ (языка без отрицания) можно дать описание работы различных алгоритмов — и в этом состоит важное значение языка без операции отрицания.
Итак, логическая система без операции логического отрицания находит свое применение при построении машинных программ. Но если взять искусственные языки, такие, как ФОРТРАН или КОБОЛ и др., которые позволяют воспользоваться высокоэффективным способом программирования, то в их состав, кроме логического сложения и логического умножения, входит и логическое отрицание, соответствующее частице «не» и обозначаемое обычно знаком  . Все инструкции о том, как произвести сборку замков, мебели, машин, инструментов, технических приборов и др., основаны на содержательном (не формализованном) использовании положительной логики.
. Все инструкции о том, как произвести сборку замков, мебели, машин, инструментов, технических приборов и др., основаны на содержательном (не формализованном) использовании положительной логики.
Дата добавления: 2014-11-13; просмотров: 325; Мы поможем в написании вашей работы!; Нарушение авторских прав |