Задача с вертикальными углами

Вот элементарный геометрический вопрос. Две пря­мые линии пересекаются и образуют два угла а и b. Мо­жете ли вы доказать их равенство?

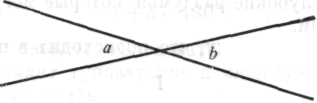
Рис. 56

Вероятно, вы изучали эту теорему в школе. Может быть, вы забыли ее — тем лучше. Попробуйте доказать ее, прежде чем вы прочтете то, что я описываю в этой главе. Возможно, тогда вы получите большее удовольст­вие от дальнейшего изложения.

Задавая этот вопрос сообразительным детям и взрос­лым, часто сталкиваешься со следующими ответами. «О чем вы спрашиваете? Разве это не очевидно? Естест­венно, что углы равны; разве это не понятно каждому?» И если вы настаиваете, то можете получить ответ: «Это совершенно ясно; две прямые линии сначала сходятся, а потом расходятся в одном и том же направлении».

Одно из основных затруднений при решении этой за­дачи заключается в том, что ученик не понимает — и не может понять — смысла вопроса. Он кажется искусствен­ным, бессмысленным. Часто в такой ситуации не могут понять, зачем требуется доказательство; многие не по­нимают или не способны понять значения доказательст­ва, потребность в котором возникла в ходе развития тео­ретической математики.

Некоторые говорят: «Конечно, вы можете доказать это, если захотите. Разрежьте лист по вертикали, переверните

половину листа и наложите один угол па другой. По­смотрите углы на свет. Вы увидите, что они совпадают». Если я говорю: «Согласен, они совпадут, но можете ли вы показать здесь, на чертеже, что они равны?» — то боль­шинство испытуемых не знают, что делать. Некоторые по-

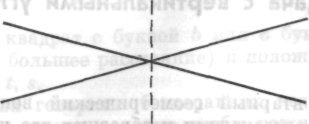
Рис. 57

гружаются в глубокие раздумья, которые могут быть мало­продуктивными.

Сначала я расскажу, что происходит в школах.

I

Учитель доказывает теорему. Он проводит линии, обоз­начает углы и продолжает следующим образом:

a + b =180°

b + c =180°

a = 180° - c

с =180° - b

а = с, что и требовалось доказать.

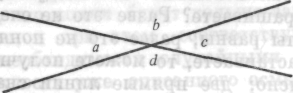
Рис. 58

Можно описать этот процесс в терминах традицион­ной логики или ассоциативной теории. Учитель показы­вает ряд последовательных операций, производит сложе­ния, пишет равенства, преобразует их и наконец получает результат. Он может начать с аксиом или некоторых об­щих положений и применить их к данному случаю. Уче­ники заучивают доказательство и после этого могут по­вторить его.

Конечно, доказательство может быть описано в терми­нах ряда операций, и для проверки его валидности их необходимо рассмотреть. Но является ли такая совокуп­ность нескольких операций тем, что действительно отра­жает существо дела?

Через несколько дней учитель вызывает ученика к лоске и просит доказать равенство углов. Если теперь уче­ник слово в слово повторяет то, чему научил его учитель, то мы не знаем, повторяет ли он услышанное слепо, раб­ски или же действительно постиг доказательство, понял его.

Бывает, что ученик не вспоминает доказательство точ­но и пишет:

a + b = 180°

c + d = 180°

затем смело говорит: «Следовательно, а—c». Другие те­ряются, выглядят туповатыми и сконфуженными. Неко­торые могут написать:

a + b = 180°

b + c = 180°

а = 180° - b

b = 180° - c

и оказываются в равной степени беспомощными ¹.

Но вы также сталкиваетесь со следующими дейст­виями:

a + d= 180°

с + d= 180°

а =с

Некоторые ученики, видя это, смеются: «Посмотрите! Он сделал две ошибки!» Но действительно хороший ученик говорит или, может быть, говорит себе: «Почему я должен заботиться о словах. Неважно, как я это сделаю». Учитель спрашивает, не может ли он написать доказательство точно в той форме, в которой оно было дано, и он уверен­но пишет:

b + c = 180°

c + d = 180°

b = d

¹ Ср. гл. 1, с. 42 и сл. Такие нелепые действия, вообще говоря, не характерны для поведения детей; они могут возникнуть глав­ным образом в результате механических упражнений.

Это, конечно, оригинально, но явно отличается от тех из­менений, которые внес первый ученик.

Мы видим, что дело не в «количестве ошибок». Одна ошибка может делать ответ совершенно бессмысленным; вместе с тем две «ошибки» могут привести или не приве­сти к успеху, действия могут быть осмысленными или бес­смысленными. Две «ошибки» могут иногда указывать на осмысленное понимание. Что же является в данном слу­чае решающим? Вернемся к этому вопросу позже.

Находятся ученики, которые приходят в замешатель­ство, если учитель использует чертеж с непривычными обозначениями. Это не является доказательством того, что «разум целиком управляется привычками» ¹. Это до­казывает, что отдельные индивиды слепо следуют «тому, чему их учили». Другие могут слегка удивиться измене­ниям, но то, что они пытаются сделать, отличается от подражательного, бессмысленного повторения.

Вот примеры А- и B-решений.

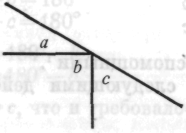
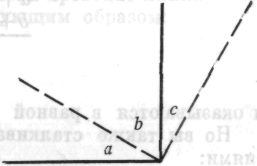
Рис. 59 Рис. 60

1. Дана прямая линия; две другие линии образуют известный угол, например 90°. Если ученик смело использует здесь выученное доказательство, то он показывает, что ничего не понял.

Это — B-задача.

2. Дан прямой угол. Две пунктирные линии также об­разуют прямой угол. Одни ученики отказываются от по­пыток: «Но, учитель, мы этого не проходили». Другие же действуют содержательно, несмотря на сильно изменен­ную ситуацию.

Это — A-задача.

¹ Thorndike E. L. The psychology of algebra. New York, Macmillan, 1920, p. 458. (См. гл. 6 о Торндайке).

Рис. 61

3. Чертится угол а, одну из его сторон продолжают, образуя угол b. b делится пополам пунктирной верти­кальной линией. Добавляется четвертая линия, образую­щая с биссектрисой прямой угол. Требуется доказать ра­венство углов а и с. Читатель может сам установить, является ли этот случай А- или B-задачей.

II

Теперь я расскажу об экспериментальных результатах, которые я получил, предлагая испытуемым самостоятель­но доказать равенство двух углов, а = с. Это трудная за­дача. Большинство испытуемых не достигло успеха. Я на­деюсь, что читатель поймет почему: необходимые струк­турные операции нелегко себе представить (ср. с. 135 и сл.). В качестве иллюстрации приведу три примера.

1. Расскажу сперва об испытуемом (взрослом), кото­рый действовал в значительной степени в соответствии с классическими положениями традиционной логики. Он сказал: «Посмотрим, какими общими положениями я рас­полагаю». Спустя некоторое время он стал выписывать истинные равенства:

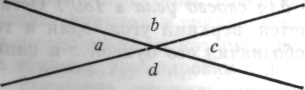Рис. 62

a+b=180° a+d=180° b+c=180° c+d=180° a+b+c+d=360° (a+b)-(c+d)=0

Затем он начал производить перестановки, комбиниро­вать равенства парами, складывать их, вычитать, следя за

тем, не выйдет ли из этого чего-нибудь. Наконец он при­шел к равенству b = d, но и не подумал остановиться здесь и продолжал свои действия, пока не получил а = с.

Эти действия были похожи на ответ, который один композитор дал любопытному посетителю, пожелавшему знать, как тот сочиняет свои мелодии. Композитор, утом­ленный посетителем, сказал: «О, это очень просто: я беру несколько нот и по-разному их комбинирую».

2. Вот отличный пример осмысленно развивающегося процесса. Испытуемый, к счастью, мыслил вслух (време­нами бормотал). Сожалею, что я не могу хорошо описать изменения в выражении его лица и голоса в ходе работы.

Глядя на чертеж, он медленно сказал: «Итак, это не отдельные углы, относительное положение которых про­извольно». Когда его спросили, что он имел в виду, он нарисовал:

Рис. 62А Рис. 62Б

«Они не похожи на такие углы. Они являются соответственными частями фигуры. Видно, что прямые линии пересекаются. Эта прямизна линий должна быть как-то связана с равенством углов!.. Прямизна в терминах углов означает 180°…» Тогда он начертил:

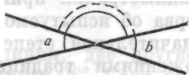
Рис. 63

в сказал: «Я вижу, что а выступает как часть для своего угла в 180°, b — как часть для своего угла в 180°! Остат­ком в обоих случаях является верхний угол, один и тот же в обоих случаях!» Он обозначил его буквой с и напи­сал два равенства:

а+с= 180° b+с= 180°

Рис. 64

Затем он продолжал: «Очевидно, что а в а + с является тем, чем b — в b+с», — и написал:

a = 180°—с

b = 180°—с

«Следовательно, — заключил он, — а = b».

3. Другая последовательность действий, первые шаги которой были весьма похожими, завершалась иначе. Ис­пытуемый понял, что следует рассматривать а и b как части 180°. Но поначалу он не понимал, что нужно рас­сматривать эти условия в связи с остатком. Он рассуж­дал следующим образом: «Я должен использовать а как часть 180°; я должен использовать b как часть 180°». Он нарисовал:

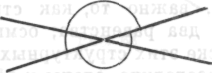
Рис. 65А

Затем он начал колебаться, говоря: «Существует еще одна возможность образования пар». Просияв, он изменил ри­сунок на:

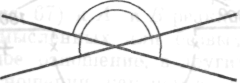
Рис. 65Б

III

Осмысленный процесс типа описанного нами в двух последних примерах включает операции группировки, осознания структуры, равенства, симметрии, «совпадения ролей», функций в группе, осознания отношений, а имен­но ρ-отношений, в которых реализуются внутренние свя­зи искомой группировки с данной структурой.

Возможно, читатель уже понял, что является сущест­венным в A- и B-случаях и реакциях. В А- и B-реакциях (см. рис. 59—61) имеет значение не повторение пунктов, не копирование заученной совокупности шагов, а струк-

турные вопросы. Для установления равенства а и с один из углов, угол а, рассматривается как часть 180°, как часть угла а+b+ с также рассматривается как часть 180° — угла c+b. При одинаковом остатке углы а и с должны быть равны. Структурный результат заключается в сле­дующем:

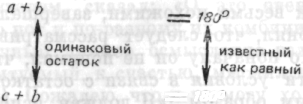
Рис. 66

Таким образом, важно то, как структурно связаны друг с другом эти два равенства; осмысленное действие заключается в поиске этих структурных требований. B-реакции нарушают последние, слепы к ним. A-реакции оп­ределяются ими, но внутри A-реакций оперирование фа­зами весьма свободно; несущественно, «правильно ли повторяются» шаги доказательства.

В общем виде структура такова:

Рис. 67

Решающее значение имеет не природа составных частей, а тип группировки в связи с отношениями:

r₁, равенством подцелых,

r₂, идентичностью остатка,

ведущими к r₃, равенству двух углов.

Это не простая совокупность отношений или операций: она взаимосвязаны с заданием, являются осмысленными час­тями замкнутого целого.

Некоторые теоретики признают необходимость целост­ного взгляда, но тем не менее упускают самое главное. Они описывают некоторые B-реакции следующим обра­зом: «Испытуемый ошибся, потому что не принял во внимание все элементы или отношения». Все элементы?

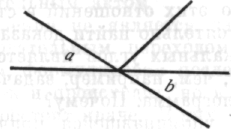
Рис. 68

Все отношения? Но для осмысленных процессов как раз характерно то, что не принимаются в расчет все элементы. Когда дан этот рисунок и требуется доказать, что а = b, на пятую линию не обращают внимания. Короче говоря, «целое» не значит «все», но относится к структуре тех единиц, которые связаны с заданием; оно относится к «хорошему гештальту».

Читателю станет ясно, если он применит эту струк­турную схему (рис. 67) к А- и B-реакциям. В некоторых B-случаях — бессмысленных или безвыходных — отсутст­вует одно основное отношение, в других — присутствуют два основных отношения, как показано на рис. 69.

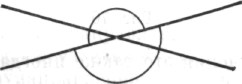
Рис. 69

Но действия оказываются слепыми потому, что неверно выбрано место единиц, которые они связывают. Это значит, что решающими являются не отношения сами о себе, а отношения в зависимости от их места в рамках хорошей структуры.

На рис. 67 отношение 1 является не отношением меж­ду элементами, а отношением между двумя группами,

или подцелыми, которые рассматриваются как симметрич­ные. Их равенство (отношение 1) играет в этом процессе решающую роль, каким бы по величине ни был угол (эле­мент), равным ли 180°, 90° и т. д. Отношение 2 является отношением между «гомологичными» единицами двух подгрупп. Из отношения 1 и 2 следует искомое отношение 3: r₁ r₂ É r₃. (Логик не должен заблуждаться относительно формулы: из r₁ r₂ следует r₃. Это не случай логи­ческого следования. Формула лишена смысла, если не учитывается место этих отношений в структуре.)

Задание самостоятельно найти доказательство теоремы о равенстве вертикальных углов является, видимо, гораз­до более трудным, чем, например, задача на определение площади параллелограмма. Почему?

Помимо ранее упоминавшейся причины, заключаю­щейся в том, что требование доказательства вообще часто остается совершенно непонятным, главная причина, по-видимому, состоит в том, что в этой ситуации следует рассматривать чертеж как две симметричные по смыслу конфигурации ab/bc, которые перекрываются, и поэтому сохраняется возможность совместного рассмотрения нуж­ных углов а и с.

Понимание того, что угол а «играет в ab такую же роль, как с — в bс», требует значительной ясности мыш­ления ¹. Некоторые испытуемые помогают себе, рисуя две фигуры:

Рис. 70

И в процессе обучения это также иногда способствует по­ниманию.

IV

Решающим в А- и B-реакциях была структурная связь пар равенств. Но этого недостаточно. В реальных случаях сама идея первого равенства, идея группировки данного угла с третьим, часто возникает потому, что для обоих рассматриваемых углов это может быть проделано сим­метричным образом. Эта операция не является операцией в себе и для себя, но находит свое оправдание как часть плана. Испытуемый чувствует, что эти две операции (позднее — равенства) будут связаны друг с другом и, та­ким образом, приведут к решению. Это не два последо­вательных акта, но, когда осуществляется первый, он уже предстает как один из членов пары. Хотя операция фик­сируется отдельной формулой, на самом деле она не яв­ляется самостоятельным актом.

Процесс мышления не является, как считают многие, простым последовательным переходом от одного пункта к другому путем формулировки последовательных суж­дений; иногда так и происходит, но в актах подлинного мышления дело обстоит иначе. В них действие начинает­ся с рассмотрения целостных свойств, а отдельные эле­менты рассматриваются в качестве частей целого.

Рис. 71

Ход мышления, его направление является в этом слу­чае не одной последовательной операцией; существует симметричная двунаправленность: каждый из двух нуж­ных углов рассматривается как часть целого, образован­ного введением третьего угла, который впоследствии мо­жет быть вычтен в силу смысловой симметрии операций.

Аналогично некоторые действия требуют совместной, симметричной кооперации обеих рук, дополняющих дви­жения друг друга. В некоторых случаях было бы бес-мысленно действовать посредством простого перехода от одной отдельной операции к другой. Вы даете ребенку две игральные карты и просите его «сделать домик». Ре-

бенок может взять одну из карт и наклонить ее примерно на 30° от вертикали, то есть произвести действие, которое является осмысленным только в связи с идеей завершен­ной структуры. Такое действие лишь с одной из карт без понимания того, что будет проделано с другой, является бессмысленным. Существуют испытуемые, которым в ходе обучения привили привычку действовать только последо­вательно, шаг за шагом, это мешает их мышлению. Не следует считать, что мы всегда должны совершать одно действие за другим, думая: «Я позабочусь о других вещах позже». Постарайтесь сначала понять, что вы делаете в данном контексте, рассматривайте вещи как части этого контекста.

Привычка к последовательности, равно как и широко распространенная теория, согласно которой мышление по своей природе является последовательным ¹, возникает вследствие ее адекватности ситуациям последовательного сложения, в которых выполнение одной из операций свя­зано с выполнением других аддитивным образом. Эта при­вычка возникает, далее, из-за того, что мы не можем про­изнести одновременно два предложения, потому что мы не можем одновременно написать два утверждения, пото­му что в описании должны переходить от одной вещи к другой. В этом одна из причин того, почему часто так по­лезны всякого рода схемы.

Далее, привычка к простой последовательности неред­ко вызывается требованием точности, правильности каж­дого шага, что, конечно, является весьма серьезным и необходимым, но оказывается недостаточным. И наконец, она возникает потому, что правильные выражения, или логические, формальные выражения, оказываются воз­можными лишь по отношению к суммам единиц. Повто­ряем: они связаны с аксиоматическим допущением, со­гласно которому мышление является и должно быть вербальным по своей природе, и логика обязательно свя­зана с языком. Оба эти предположения являются невер­ными обобщениями. По-видимому, понятие целого не поддается формальному описанию.

¹См. формулировкуКанта, согласно которому мышление по необходимости является только дискурсивным.