Примеры 5 страница

Анализ частей схемы ясно показывает, что левая и правая фигуры сильно отличаются друг от друга. Это от­носится не только к фигурам в целом — параллелограмму и прямоугольнику, — но также и к их отдельным частям. Если читатель изучит и сравнит значения линий, он будет очень удивлен тем, как сильно отличаются роли этих линий в левой и правой частях схемы. Укажу только не­сколько отличий. Линии 1 и 6 слева являются граница­ми; справа они сливаются и исчезают в процессе заверше­ния прямоугольника. Слева линии 1, 5, 6, 2—7 образуют фигуру и появляются линии 3—4, тогда как справа фи­гуру образуют линии 4, 5, 3, 7—2, а линия 6—1 исчезает. Равенство игнорирует тот факт, что эти линии совместно образуют границы фигуры, а это обстоятельство имеет важное значение для фигур, площадь которых необходи­мо определить.

Так обстоит дело и с углами: их значение и функции в двух фигурах совершенно различны; углы, которые иг­рают важную роль в левой, в правой исчезают, и т. д.

Если провести точный анализ всех таких факторов, то обнаружится огромное число структурных различий. Если их рассматривать по отдельности, то они будут ка­заться очень сложными. Очень трудно, да и, по всей ве­роятности, невозможно было бы прийти к ясному процес­су, если начинать с простой суммы таких детализирован­ных особенностей. Но если подходить к проблеме «сверху», исходя из целостных свойств фигур и функционального значения линий и т. д., то эта пугающая каждого слож­ность исчезает.

3) В продуктивных процессах основным является из­менение, которое происходит, когда a+b превращается в b+а. Для фигур мы имеем не просто отношение равен­ства двух вещей, как в формуле, а направленное изме-

a + b → b + a

и к тому же еще и необходимое.

Это переход к чему-то совершенно иному. Мы имеем не просто равенство, а переход. И хотя проблема валид­ности очень важна, она, в сущности, игнорирует такую направленность. В этом и заключается основное отличие нашего подхода от традиционного логического подхода. В то время как традиционную логику интересует глав­ным образом вопрос «равенства» (или «эквивалентности») а₁и a₂, в гештальттеории основным является переход от а₁к a₂, тот факт, что осуществился именно этот переход, и т. д. И это фундаментальное положение; оно означает принципиальный поворот от статики к рассмотрению ди­намики процесса мышления.

Но разве этот переход не подразумевает альтернативу «логичны» пли «нелогичны», осмысленны или слепы, слу­чайны действия? И разве это не является предметом ло­гики?

Такой «переход» часто связан со «структурной реорга­низацией». Здесь я хочу отметить, что это важное для гештальттеории понятие порой понимают неверно, недо­оценивая тем самым его значение. Несколько лет назад один психолог показал, как он его понимает: он предлагал заучивать ряд бессмысленных слогов сначала в одной, а затем в другой последовательности. Мы здесь под этим по­нятием подразумеваем вовсе не эту произвольную

процедуру, а такую реорганизацию, которая обусловлена структурой данной ситуации. Векторы такого изменения складываются на основе функциональных требований структуры ситуации.

И я хочу отметить, что в подобных случаях нельзя рассматривать такой переход как просто переход к более знакомой фигуре; это переход к такой форме, в которой содержание приобретает ясную структуру. Величина пло­щади, представленная в виде отдельных квадратов, ста­новится прозрачно ясной в форме прямоугольника.

4) Следует отметить, что равенство а + b — b+а дейст­вительно играет важную роль в решении проблемы, свя­занной с сущностью величины. Закон, согласно которому подобные операции не сказываются на величине, отражает структурную простоту ситуации. Но это не значит, что этот закон является необходимо истинным. Природа не обязана быть столь простой. То, что истинно в отноше­нии суммы — а здесь мы имеем дело с величиной площа­ди, которая по своей природе является аддитивной, — не является истинным вообще, не является истинным для того, что имеет неаддитивную природу. Различия между порядком bа и порядком ab, хотя и не имеют зна­чения в случае величины, так как величины аддитивны, весьма существенны для других аспектов процессов мыш­ления. В самом деле, порядок часто оказывает гораздо большее влияние на объект, характер его частей и соот­ветствующую динамику, чем в нашем случае. В рассмот­ренном примере в результате изменения мы снова полу­чаем замкнутую фигуру. Сравните этот случай с двумя способами изменения порядка ab на bа в следующих про­стых примерах:

Рис. 41

И совершенно нелепо думать, что закон коммутативности имеет силу, скажем, для мелодий. Это относится и ко многим другим случаям. С этим вопросом связаны серь­езные, фундаментальные логические проблемы. Некото­рые из них, вроде тех, которые выше проиллюстрированы на примере шестиугольника и ромба, частично исследо­вались в современной теории сетей отношений и других исследованиях, однако более глубокие проблемы возни­кают в отношении свойств и динамики целого.

Многие до сих пор рассматривают закон коммутатив­ности как общий основной закон логики, считая, что фак­ты, суждения и т. д. вообще являются аддитивными, ато­марными по своей природе. Поэтому возникло даже такое представление, будто логика в основном имеет дело с «тавтологиями». В свете нашего обсуждения ясно, что этот взгляд, по-видимому, совершенно не учитывает реаль­ные проблемы мышления.

Закон коммутативности не распространяется, конечно, на элементы реального процесса мышления. Если бы кому-то вздумалось смешать все элементы, операции или фазы реального процесса мышления, а затем устанавли­вать равенство, пользуясь законом коммутативности, то полученный результат оказался бы совершенно ложным. Элементы такого процесса не являются простой суммой отдельных частей.

5) Для логика закон коммутативности является од­ним из суждений, образующих доказательство. Тут сле­дует сказать, что и само доказательство имеет свою струк­туру. Если субъект не видит структуру доказательства, то оно не будет достигнуто. Сталкиваясь с рядом сужде­ний, которые образуют доказательство, ученик зачастую испытывает удивление, досадует и приходит в замеша­тельство. Он читает формулировки, проверяет их по чер­тежу, читает теоремы, пытается согласовать отдельные части, как картинку-загадку, чтобы получить осмыслен­ный контекст. Если ему это не удается, он может запом­нить формулировки в данной последовательности; восста­навливая доказательство, он может отчаянно пытаться вспомнить, какое утверждение в учебнике следует даль­ше: если ему это не удается, он может сформулировать другие утверждения, которые, хотя и являются вполне правильными, в данном контексте совершенно бессмыс­ленны. Способный ученик, конечно, делает то, что требует­ся, но он приходит к этому сам. Он должен превратить

простую сумму утверждений в осмысленную структуру до­казательства. Эта операция предполагает разумную груп­пировку, понимание функциональной иерархии, направле­ния, в котором движется доказательство, места, роли, функции, смысла каждого утверждения в структуре. Если человек не может понять, скажем, что одно из утвержде­ний в совокупности с некоторыми другими утверждениями принадлежит к одному блоку доказательства (например, относящемуся к подобию треугольников), и группирует их неверно, то он весьма далек от понимания. Иногда испы­туемые пытаются каким-то образом упорядочить утверж­дения только о линиях, затем об углах, потом о плоско­стях и гордятся тем, что им удалось установить какой-то логический порядок, но, вспомнив о задании, вновь впа­дают в отчаяние. Отнюдь не маловажно понять, какую функцию выполняет данное утверждение: является ли оно посылкой или выводом, который в свою очередь ста­новится в дальнейшем посылкой, и т. д.

Аналогичные соображения справедливы и в отноше­нии процесса поисков доказательства. Осмысленные по­иски доказательства не осуществляются таким способом, который был описан выше и который столь характерен для традиционного логического подхода. Дело совсем не в том, чтобы формулировать верные утверждения, вспом­нить выученные теоремы и г. д. Подлинное открытие возникает в результате осознания требований, которым должно удовлетворять само доказательство, необходимо­сти привести факты в осмысленную связь.

Но в то время, как структура доказательства в нашем примере определения площади параллелограмма являет­ся сравнительно простой, в других случаях не так легко найти психологически адекватную, структурно осмыслен­ную процедуру. Здесь настоятельно необходимы творче­ские поиски ¹.

40. Мы обсудили факторы, которые играют важную роль в решении задачи, в достижении цели. Но что мож­но сказать о самой цели? Часто мыслительные процессы рассматриваются как процессы решения задачи, достиже-

¹ В течение нескольких лет я касался этих вопросов в своих лекциях по психологии обучения и исследовал их со своими коллегами. Д-р Джордж Катона рассматривает некоторые из этих во-

ния поставленной цели; до сих пор и мы поступали так же. Согласно многим теориям, именно в этом заключается задача мышления. Но разве наши проблемы не повторя­ются в отношении самой цели?

В нашем примере скромной геометрической задачи ситуация вообще является достаточно простой. Здесь до­ставляет удовольствие сам процесс решения задачи, ра­дует достижение цели, проверка своих умственных спо­собностей. В этом смысле мышление может быть относи­тельно замкнутым процессом. Более того, в некоторых случаях задача сохраняет смысл и в более широком кон­тексте. Так обстоит дело, когда задача на определение площади рассматривается в контексте землемерных ра­бот или когда этот вопрос возникает в более широком контексте геометрического мышления — например, когда понят способ определения площади прямоугольника и встает вопрос об определении площади других фигур.

Но в некоторых ситуациях бессмысленно решать за­дачу определения площади параллелограмма, потому что такая задача не соответствует структуре данной ситуации, потому что эта цель неуместна и ситуация требует дру­гих действий. Если в такой ситуации дается это задание или так или иначе возникает вопрос о площади, некото­рые люди, не замечая, что требуется в ситуации, начи­нают определять площадь и слепо следуют намеченной цели. Однако мы часто наблюдаем и разумные реакции, когда испытуемый отказывается решать такую задачу и сосредоточивает свое внимание на том, что действительно важно в данной ситуации ¹.

Я приведу простой пример. Учитель охотно пользу­ется любой возможностью решать практические задачи. На последнем уроке он показал ученикам, как опреде­ляется площадь трапеции при помощи вспомогательных

просов в своей книге "Organizing and memorizing" (New York, Co­lumbia University Press, 1940) и в следующих статьях: "On diffe­rent forms of learning by reading", ("Journal of Educational Psycho­logy", 1942, vol. 33, p. 335—355); "The role of the order of presenta­tion in learning", (American Journal of Psychology, 1942, vol. 55, p. 328—353). Д-р Катрин Штерн сообщила о своей работе по обу­чению арифметике в докладе на заседаниях Восточной психологи­ческой ассоциации, состоявшихся в 1941 г. Этот доклад является частью ее книги "Children discover arithmetic". New York, Harper, 1949 — Прим. Майкла Вертгеймера. ¹ См. пример в гл. 4, с. 170.

линий, вывел формулу 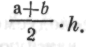Теперь он указывает на висящую на стене картину в раме и говорит: «Мне нуж­но определить площадь рамы». Он обозначает линии бук­вами а, b, с, d, сообщает их длину и добавляет: «Видите, тут четыре трапеции. Надеюсь, что вы помните, как опре­деляется их площадь».

Рис. 42

Некоторые дети старательно выполняют задание учи­теля; они нудно вычисляют площадь — некоторые оши­баются и с напряженным вниманием исправляют ошибки. Но других детей это, видимо, забавляет, они ничего подобного не делают, а перемножают с с d, и а с b, вычи­тают аb из cd и говорят: «Вот так! Зачем вычислять пло­щади этих трапеций?»

Мышление — это не просто решение поставленных за­дач. Сама цель как часть ситуации может быть струк­турно осмысленной или бессмысленной. Как и отдельные операции в реальном процессе мышления, цель должна функционировать как часть целого, имеющая свое место и выполняющая свою роль в соответствии со структурны­ми требованиями более широкого контекста. Часто, пытаясь решить поставленную задачу, человек останавливается, осознавая, что ситуация требует совсем других действий, требует изменения самой цели. Часто упорное следова­ние поставленным целям, настойчивость в их достижении являются совершенно бессмысленными.

В жизни такие случаи нередко носят очень серьезный характер. Иногда люди, например, политики, после долгих и упорных попыток достичь определенной цели внезапно понимают, что сама эта цель в том виде, как она постав­лена, является неуместной, что она не связана с реаль­ными требованиями, с более важными целями. Уже одно это само по себе может быть открытием чего-то такого, что прежде не осознавалось, а именно открытием того, что

средства достижения преследуемой цели поставят под угрозу, уничтожат более важную цель. Мышление инте­ресуют не просто средства; его интересуют сами резуль­таты и их структурное значение.

В рассмотренных нами геометрических задачах эти вопросы не столь серьезны; мы описывали задачи, возни­кающие в спокойных, мирных, прозрачных жизненных ситуациях, задачи, в которых возможно очевидное, кри­стально ясное решение. Вот почему учителя так настоя­тельно рекомендуют изучение геометрии как средство развития умственных способностей в атмосфере четкости, очевидности, последовательности, которое может способст­вовать переносу сформированных приемов и установок мышления на более сложные и менее ясные области.

В этом одна из причин того, почему в данной книге мы выбрали для обсуждения эти простые геометрические примеры; видимо, полезнее сначала обсудить основные теоретические вопросы на структурно более простом ма­териале ¹.

¹ Дополнительный материал, имеющий отношение к данной главе, приведен в Приложениях 2, 3, 4 и 5. — Прим. Майкла Верт­геймера.