ОСНОВНОЕ УРАВНЕНИЕ ЦЕНТРОБЕЖНЫХ НАСОСОВ

Основное уравнение лопастных насосов можно вывести на основании уравнения моментов количества движения. Пусть тело М массой m (рис. 9.15) движется со скоростью С.

Рис. 9.15. Момент количества движения

Количеством движения называется вектор, равный по величине произведению массы тела на его скорость и направленный вдоль вектора скорости. Спроектировав количество движения на направление, перпендикулярное лучу, проведенному к телу М из точки О, и умножив полученную проекцию на расстояние ОМ = R, получим момент количества движения тела относительно точки О:

. (9.37)

Производная по времени от момента количества движения механической системы относительно неподвижной точки равна главному моменту всех внешних сил, приложенных к системе относительно той же точки, т.е.

. (9.38)

Используем приведенные положения механики для объема жидкости, заключенной в канал между лопастями насоса (см. рис. 9.13). Выделим контрольными поверхностями АиВ объем жидкости, находящейся в канале. Через промежуток времени объем жидкости АВ переместится в положение А'В'. Изменение момента количества движения жидкости за время dt:

. (9.39)

Момент количества движения жидкости в объеме А'В' равен сумме моментов количества движения жидкости в объёмах А'А и ВВ':

, (9.40)

а момент количества движения жидкости в объеме АВ равен сумме моментов количества движения в объемах АА' и В'В:

. (9.41)

Подставляя формулы (9.40) и (9.41) в (9.39), получаем:

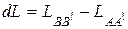(9.42)

Объем ВВ' равен объему жидкости, вытекающей через поверхность В за время dt, т.е. равен DQ dt, а масса жидкости, заключенная в объеме ВВ', равна

, (9.43)

где DQ - расход жидкости в одном межлопастном канале.

Для несжимаемой жидкости объем АА' = ВВ' и m_AA = m_BB = rDQdt.

Моменты количества движения массы жидкости, заключенной в объемах ВВ' и АА', равны соответственно:

, (9.44)

,

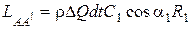где C₁cosa₁ и C₂cosa₂ - проекции абсолютной скорости на входе и выходе из рабочего колеса на направление касательной к внутренней и внешней его окружности (см. рис. 9.13); R₁ и R₂ - внутренний и наружный радиусы рабочего колеса. Подставляя формулу (9.44) в формулу (9.42), получаем:

или .

С учетом формул (9.38) и (9.34) запишем:

. (9.45)

Это изменение момента количества движения происходит за счет момента сил, с которыми стенки канала действуют на жидкость. Полученное уравнение может быть распространено на все рабочее колесо, представляющее собой систему каналов. В этом случае под Q следует понимать расход жидкости через колесо, под - момент сил, с которым рабочее колесо воздействует на находящуюся в нем жидкость (здесь n - количество межлопастных каналов). Таким образом, для рабочего колеса

. (9.46)

Секундная работа (мощность), которую производит рабочее колесо, воздействуя на находящуюся в нем жидкость, равна произведению момента М на угловую скорость рабочего колеса w. Эта работа равна энергии, передаваемой рабочим колесом жидкости за единицу времени, или гидравлической мощности N_г.

Тогда N_г = Nw или, с учетом (9.46):

. (9.47)

Так как R₁w = U₁ - окружная скорость рабочего колеса на входе и R₂w = U₂ - окружная скорость рабочего колеса на выходе, то:

. (9.48)

Ранее мы получили уравнение (9.15) ,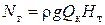

и тогда: . (9.49)

В уравнении (9.49) Н_т - напор, который создал бы центробежный насос с бесконечным числом бесконечно тонких лопастей, если бы он перекачивал абсолютно невязкую жидкость, т.е. без учета потерь напора в насосе (без учета h_г).

Уравнение (9.49) и есть основное уравнение центробежных насосов. Это уравнение впервые было получено Л. Эйлером в 1755 г. и называется уравнением Эйлера. Оно связывает напор насоса со скоростями движения жидкости, которые зависят от подачи, числа оборотов рабочего колеса, геометрии лопастей (a, R).

Уравнение (9.49) дает возможность по заданному напору, подаче и числу оборотов рассчитать выходные элементы рабочего колеса. Очертание лопастей рабочего колеса зачастую принимается таким, что жидкость входит в рабочее колесо в радиальном направлении и угол a₁ между скоростями C₁ и U₁ равен 90^о, а cos a₁ = 0. Для таких насосов

. (9.50)

Действительный напор, создаваемый рабочим колесом, меньше теоретического при бесконечном количестве лопастей Н < Н_т. Во-первых, это объясняется тем, что часть энергии, получаемой жидкостью в рабочем колесе, затрачивается на преодоление гидравлических сопротивлений в проточной части машины. Эти потери учитываются гидравлическим КПД - h_г. Во-вторых, указанное неравенство обусловлено отклонением действительной картины течения от предполагаемой струйной при бесконечном количестве лопастей. Это учитывается введением поправочного коэффициента e_z на конечное число лопастей.

. (9.51)

Гидравлический КПД современных центробежных машин оценивает гидравлическое совершенство проточной части их и лежит в пределах 0,80-0,96. Поправочный коэффициент e_z < 1 зависит от конструкции рабочего колеса и определяется по полуэмпирическим формулам, например по формуле Стодолы:

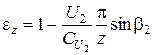, (9.52)

где z - число лопастей, b₂ - угол между относительной и окружной скоростями на выходе из рабочего колеса, т.е. угол, который характеризует кривизну лопасти (рис. 9.16).Остальные обозначения приведены выше. Значение поправочного коэффициента e_z в ориентировочных расчетах можно принять e_z = 0,8 - 0,7.