КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства выборочного коэффициента корреляции
1.  или
или 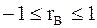 .
.
2. Если  , тогда
, тогда 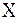 и
и  не связаны линейной корреляционной зависимостью (но могут быть связаны нелинейной корреляционной или даже функциональной зависимостью).
не связаны линейной корреляционной зависимостью (но могут быть связаны нелинейной корреляционной или даже функциональной зависимостью).
3. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при  переходит в линейную функциональную зависимость.
переходит в линейную функциональную зависимость.
4. Если 
 , тогда
, тогда 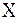 и
и  связаны прямой (обратной) линейной функциональной зависимостью.
связаны прямой (обратной) линейной функциональной зависимостью.
Свойства математического ожидания
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:
 .
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания .
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания
 .
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: .
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
 .
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых .
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых
 .
Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
ТеоремаМатематическое ожидание М (X) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: .
Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
ТеоремаМатематическое ожидание М (X) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
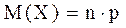 . .
| Свойства дисперсии
Свойство 1. Дисперсия постоянной величины С равна нулю:
 .
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: .
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
 .
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: .
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
 .
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин. .
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.
 .
Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины: .
Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:
 .
Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: .
Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
 .
ТеоремаДисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: .
ТеоремаДисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:
 . .
| ||||||||||||||||||||
Числовые характеристики основных распределений дискретных случайных величин
Приведем без вывода основные числовые характеристики дискретных случайных величин:
1) биномиальное распределение
 , k=0, 1, 2, …, n, , k=0, 1, 2, …, n,
 , ,  , , 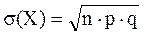 ;
2) распределение Пуассона ;
2) распределение Пуассона
 , k=0, 1, 2, …, , k=0, 1, 2, …,
 , ,  , ,  ;
3) геометрическое распределение ;
3) геометрическое распределение
 , k=0, 1, 2, …, , k=0, 1, 2, …,
 , ,  , ,  ;
4) гипергеометрическое распределение ;
4) гипергеометрическое распределение
 , m=0, 1, 2, ..., М, , m=0, 1, 2, ..., М,
 , ,  . .
| Модой дискретнойслучайной величины называется ее наиболее вероятное значение.
Медианой дискретнойслучайной величины называется ее наиболее вероятное значение.
Медианой случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е. случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е.
 .
ПРИМЕРНайти математическое ожидание и дисперсию случайной величиныX, которая задана следующим законом распределения: .
ПРИМЕРНайти математическое ожидание и дисперсию случайной величиныX, которая задана следующим законом распределения:
Решение. Найдем математическое ожидание
Напишем закон распределения случайной величины X2:
Найдем математическое ожидание
Искомая дисперсия
|
Задача
Задача: Точечная оценка параметра распределения  . Тогда его интервальная оценка может иметь вид:
Ответы: 1). . Тогда его интервальная оценка может иметь вид:
Ответы: 1).  2). 2). 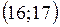 3). 3).  4). 4).  5). нет правильного ответа
Решение:
Т.к. точечная оценка параметра распределения
5). нет правильного ответа
Решение:
Т.к. точечная оценка параметра распределения  должна входить в заданный интервал, то ответ №1. должна входить в заданный интервал, то ответ №1.
| Задача
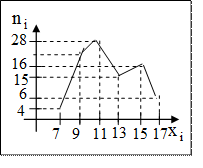 Задача: Из генеральной совокупности извлечена выборка объема Задача: Из генеральной совокупности извлечена выборка объема  , полигон частот которой имеет вид:
Найти частоту варианты , полигон частот которой имеет вид:
Найти частоту варианты  Ответы: 1). 20 2). 22 3). 24
4). 21 5). нет правильного ответа
Решение:n2=90-4-6-15-16-28=21
Ответ №4
Ответы: 1). 20 2). 22 3). 24
4). 21 5). нет правильного ответа
Решение:n2=90-4-6-15-16-28=21
Ответ №4
|
Вычисление пределов
ПРИМЕР 2.41.Найти  .
Решение. Пределы числителя и знаменателя при .
Решение. Пределы числителя и знаменателя при 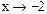 равны нулю. Следовательно, имеем неопределенность вида равны нулю. Следовательно, имеем неопределенность вида 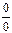 . Для раскрытия неопределенности разложим числитель и знаменатель на множители и сократим на общий множитель . Для раскрытия неопределенности разложим числитель и знаменатель на множители и сократим на общий множитель  . Имеем . Имеем   . .
| ПРИМЕР 2.45. Найти  .
Решение. Для раскрытия неопределенности .
Решение. Для раскрытия неопределенности  избавимся от иррациональности в числителе путем умножения числителя и знаменателя на избавимся от иррациональности в числителе путем умножения числителя и знаменателя на  . Получим . Получим   . .
|
ПРИМЕР 2.48.Найти  .
Решение. Имеем неопределенность вида .
Решение. Имеем неопределенность вида  . Разделив числитель и знаменатель дроби на . Разделив числитель и знаменатель дроби на 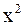 , получим , получим
  . .
| ПРИМЕР 2.49. Найти предел  Решение.
Решение. 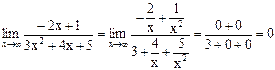 .
ПРИМЕР 2.50. Найти предел .
ПРИМЕР 2.50. Найти предел  Решение.
Решение.  . .
|
ПРИМЕР 2.51. Найти предел дробно-рациональной функции  .
Решение. Имеем .
Решение. Имеем   . .
|
Таблица основных интегралов
1  , ,  , (1.10)
2 , (1.10)
2  (1.11)
3 (1.11)
3 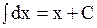 (1.12)
4 (1.12)
4  , ,  , (1.13)
5 , (1.13)
5  (1.14)
6 (1.14)
6 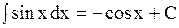 (1.15)
7 (1.15)
7 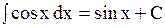 (1.1 (1.1
| 8  (1.17)
9 (1.17)
9 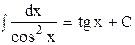 (1.18)
10 (1.18)
10 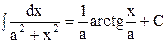 (1.19)
11 (1.19)
11 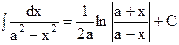 , ,  (1.20)
12 (1.20)
12  , ,  (1.21)13 (1.21)13  , ,
| 14  ,
15 ,
15  (1.24)
16 (1.24)
16  (1.25)
17 (1.25)
17  (1.26)
18 (1.26)
18  (1.27)
19 (1.27)
19  (1.28)
20 (1.28)
20 
|
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Комплексным числом  называется выражение вида называется выражение вида
 , (2.1)
где , (2.1)
где  и и 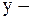 действительные числа, а действительные числа, а  мнимая единица, определяемая равенством мнимая единица, определяемая равенством 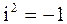 или или  . Числа . Числа  и и  называются действительной и мнимой частями комплексного числа называются действительной и мнимой частями комплексного числа  и обозначаются и обозначаются  , , 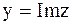 .
Форму (2.1) комплексного числа .
Форму (2.1) комплексного числа  называют алгебраической. Два комплексных числа называют алгебраической. Два комплексных числа  и и  считаются равными, если равны их действительные и мнимые части: считаются равными, если равны их действительные и мнимые части:  . Число . Число  при условии при условии  .
Понятия “больше” и “меньше” для комплексных чисел не устанавливаются.
Число .
Понятия “больше” и “меньше” для комплексных чисел не устанавливаются.
Число  называется сопряженным числу называется сопряженным числу  .
Алгебраические действия над комплексными числами определяются следующими равенствами: .
Алгебраические действия над комплексными числами определяются следующими равенствами:
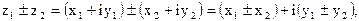


 Комплексное число Комплексное число  изображается точкой изображается точкой  на координатной плоскости на координатной плоскости  (рис. 2.1). При этом действительные числа (рис. 2.1). При этом действительные числа  изображаются точками на оси изображаются точками на оси  , называемой здесь действительной осью, а мнимые числа , называемой здесь действительной осью, а мнимые числа 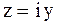 изображаются точками оси изображаются точками оси  , называемой мнимой осью. Плоскость, на которой изображают комплексные числа, называется комплексной плоскостью. , называемой мнимой осью. Плоскость, на которой изображают комплексные числа, называется комплексной плоскостью.
 (2.5)
Комплексному числу (2.5)
Комплексному числу  не приписывается какое-либо значение аргумента.
Зная модуль комплексного числа не приписывается какое-либо значение аргумента.
Зная модуль комплексного числа   и главное значение его аргумента и главное значение его аргумента  , мы можем вычислить его действительную часть , мы можем вычислить его действительную часть  и мнимую и мнимую  : :
 и записать число и записать число  в форме в форме
 (2.6) Эту форму комплексного числа называют тригонометрической.
Имеют место следующие правила умножения, деления, возведения в целую положительную степень и извлечение корня для чисел (2.6) Эту форму комплексного числа называют тригонометрической.
Имеют место следующие правила умножения, деления, возведения в целую положительную степень и извлечение корня для чисел  в тригонометрической форме: в тригонометрической форме:
 , (2.7) , (2.7)
 , (2.8) , (2.8)
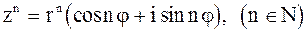 , (2.9) , (2.9)
 , (2.10) где , (2.10) где  .
Формула (2.9) называется формулой Муавра.
Примеры решения задач
ПРИМЕР 2.2.Найти .
Формула (2.9) называется формулой Муавра.
Примеры решения задач
ПРИМЕР 2.2.Найти 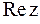 и и  , если , если  .
Решение. .
Решение.  , откуда , откуда
 .
ПРИМЕР 2.3. Выяснить геометрический смысл модуля разности .
ПРИМЕР 2.3. Выяснить геометрический смысл модуля разности  двух комплексных чисел двух комплексных чисел 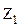 и и  .
Решение. .
Решение. 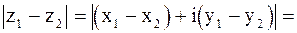
 . Следовательно, . Следовательно,  означает расстояние между точками означает расстояние между точками  и и  (рис. 2.2) (рис. 2.2)
 Если изобразить комплексное число с помощью вектора, то действительная и мнимая части Если изобразить комплексное число с помощью вектора, то действительная и мнимая части  являются координатами вектора, а так как при вычитании векторов их координаты соответственно вычитаются, то вычитание комплексных чисел сводится к вычитанию векторов, изображающих эти числа. Как видно из рис. 2.2., являются координатами вектора, а так как при вычитании векторов их координаты соответственно вычитаются, то вычитание комплексных чисел сводится к вычитанию векторов, изображающих эти числа. Как видно из рис. 2.2., 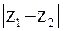 есть длина вектора есть длина вектора  , иначе расстояние между точками, изображающими числа , иначе расстояние между точками, изображающими числа 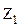 и и  . .
 .
.
| Комплексное число  может быть изображено вектором может быть изображено вектором  с координатами с координатами  и и  и с началом в точке и с началом в точке  (рис. 2.1).
Длина (рис. 2.1).
Длина  вектора вектора  , изображающего комплексное число , изображающего комплексное число  , называется модулем комплексного числа. Угол , называется модулем комплексного числа. Угол  , образуемый этим вектором с положительным направлением действительной оси, называется аргументом комплексного числа. Модуль числа принято обозначать , образуемый этим вектором с положительным направлением действительной оси, называется аргументом комплексного числа. Модуль числа принято обозначать  , а аргумент , а аргумент  .
Для модуля и аргумента, как видно на рис. 2.1, справедливы формулы .
Для модуля и аргумента, как видно на рис. 2.1, справедливы формулы
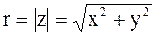 , (2.2) , (2.2)
 (при (при  ) (2.3)
Величина ) (2.3)
Величина  имеет бесчисленное множество значений, отличающихся одно от другого на целое, кратное имеет бесчисленное множество значений, отличающихся одно от другого на целое, кратное  . Если величину одного из углов обозначить через . Если величину одного из углов обозначить через  , то совокупность величин всех углов запишется в следующем виде: , то совокупность величин всех углов запишется в следующем виде:
 Значение
Значение  , принадлежащее промежутку , принадлежащее промежутку  , называется главным и обозначается , называется главным и обозначается  . Итак, . Итак, 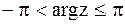 , ,
 (2.4)
Зная действительную часть (2.4)
Зная действительную часть  и мнимую часть и мнимую часть  комплексного числа комплексного числа  и пользуясь тем, что и пользуясь тем, что  , можем вычислить , можем вычислить  по формуле
Геометрически по формуле
Геометрически  значений выражения значений выражения 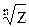 (2.10) изобразятся вершинами некоторого правильного (2.10) изобразятся вершинами некоторого правильного  угольника, вписанного в окружность, с центром в начале координат и с радиусом угольника, вписанного в окружность, с центром в начале координат и с радиусом 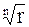 . В теории функций комплексного переменного известны формулы Эйлера . В теории функций комплексного переменного известны формулы Эйлера
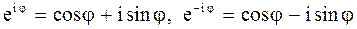 . (2.11)
С помощью первой формулы Эйлера, умножив левую и правую части на . (2.11)
С помощью первой формулы Эйлера, умножив левую и правую части на  , можно перейти от тригонометрической формы (2.6) к показательной форме комплексного числа , можно перейти от тригонометрической формы (2.6) к показательной форме комплексного числа
 . (2.12)
В виду ее компактности она удобнее равносильной тригонометрической формы.
Алгебраические действия (2.7) - (2.10) с помощью показательной формы (2.12) имеют более простой вид . (2.12)
В виду ее компактности она удобнее равносильной тригонометрической формы.
Алгебраические действия (2.7) - (2.10) с помощью показательной формы (2.12) имеют более простой вид
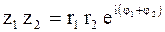 , (2.13) , (2.13)
 , (2.14) , (2.14)
 , (2.15) , (2.15)
 (2.16)
При решении задач полезно помнить, что (2.16)
При решении задач полезно помнить, что   и т.д.,. и вообще при любом целом и т.д.,. и вообще при любом целом   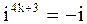 .
ПРИМЕР 2.4.Найти модуль и главное значение аргумента комплексного числа .
ПРИМЕР 2.4.Найти модуль и главное значение аргумента комплексного числа  ; представить его в тригонометрической и показательной формах.
Решение. По определению модуля, ; представить его в тригонометрической и показательной формах.
Решение. По определению модуля,  . Так как значение аргумента . Так как значение аргумента  удовлетворяют соотношению удовлетворяют соотношению 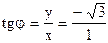 то то  . Итак, . Итак,  и согласно (2.6) и (2.12) имеем и согласно (2.6) и (2.12) имеем  .
ПРИМЕР 2.5. Выполнить действия умножения и деления комплексных чисел .
ПРИМЕР 2.5. Выполнить действия умножения и деления комплексных чисел  и и  , представив их вначале в тригонометрической форме.
Решение. , представив их вначале в тригонометрической форме.
Решение. 
 . Применяя формулы (2.7) и (2.8), получим . Применяя формулы (2.7) и (2.8), получим
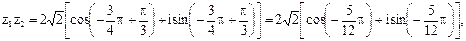
 ПРИМЕР 2.6. Вычислить
ПРИМЕР 2.6. Вычислить  .
Решение. Запишем число .
Решение. Запишем число  в тригонометрической форме. По формуле (2.9) имеем в тригонометрической форме. По формуле (2.9) имеем  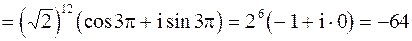 . .
|
ЗАДАНИЕ N 18 (  - выберите варианты согласно тексту задания) Укажите соответствие между областями и их геометрическими интерпретациями 1) - выберите варианты согласно тексту задания) Укажите соответствие между областями и их геометрическими интерпретациями 1)  2) 2)  3) 3) 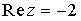 4) 4)  Решение: Т.к.
Решение: Т.к.  , то ось Ох – действительная, ось Oy – мнимая.
1) , то ось Ох – действительная, ось Oy – мнимая.
1)  (Полоса вдоль оси Х, (Полоса вдоль оси Х,  ) Ответ: С 2) ) Ответ: С 2)  (Прямая y=-2) Ответ: D 3) (Прямая y=-2) Ответ: D 3) 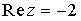 (Прямая x=-2) Ответ: E 4) (Прямая x=-2) Ответ: E 4)  (Прямая y=3) Ответ: A (Прямая y=3) Ответ: A
| |||||||||||||||
ВАРИАНТЫ ОТВЕТОВ:
|
Дата добавления: 2015-04-15; просмотров: 328; Мы поможем в написании вашей работы!; Нарушение авторских прав |


 :
: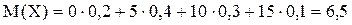 .
.
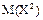 :
: .
. .
.