Екатеринбург 2009

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

Уральский государственный университет – УПИ

имени первого Президента России Б.Н. Ельцина»

Кафедра высшей математики

РАСЧЕТНАЯ РАБОТА №2

Дисциплина:ЕН.Ф.01 МАТЕМАТИКА. Алгебра и геометрия

Модуль 1: Алгебра: (1 зачетная единица)

Студент

Группа

Преподаватель

Вариант

Дата

Екатеринбург 2009

Составитель Трояновская Л.Ю.
Вариант 1

1. Задан тетраэдр . В базисе из ребер , и найдите координаты вектора , где и – середины ребер и .

2. Векторы образуют правую тройку, взаимно перпендикулярны, . Вычислить .

3. Даны точки и . Найти проекцию вектора на вектор .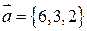

4. Найти уравнения и длины сторон и медиан треугольника, если даны три вершины .

5. Построить кривую.

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L

8. Точка служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.

9. Вычислите расстояние от точки до прямой

10. Докажите, что прямая лежит в плоскости

11. Составить уравнение сферы, если известны координаты центра и радиус .

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 2

1. Задан тетраэдр . В базисе из ребер и найти координаты вектора , где F – точка пересечения медиан основания АВС.

2. Вычислить направляющие косинусы вектора .

3. Вычислить

4. Найти вершины, и уравнения медиан треугольника, если даны уравнения трех сторон .

5. Построить кривую .

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L

8. Укажите значение , при котором плоскости : и : будут перпендикулярными.

9. Составьте уравнения прямой, образованной пересечением плоскости с плоскостью, проходящей через ось OX и точку

10. Найдите точки пересечения прямой с координатными плоскостями.

11. Составить уравнение сферы, если известны координаты центра и точки на сфере .

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 3

1. В тетраэдре медиана AL грани АВС делится точкой М в отношении . Найти координаты вектора в базисе из ребер .

2. Заданы векторы Вычислить 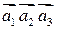. Какова ориентация троек: а) ; б) ; в) ?

3. Даны векторы 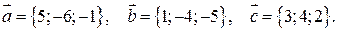Найти проекцию вектора 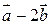на вектор .

4. Найти уравнения и длины сторон треугольника, если даны две вершины треугольника А(-1, 1), В(9, -4) и точка пересечения высот К(5, 4).

5. Построить кривую .

6. Привести кривую к каноническому виду: .

7. Найти точку, симметричную точке М относительно прямой L

8. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям

9. Докажите, что прямая пересекает ось OY.

10. Составьте уравнения прямых, образованных пересечением плоскости 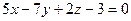с координатными плоскостями.

11. Составить уравнение сферы, если известно, что точки и – концы диаметра сферы.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями

Вариант 4

1. Дан параллелепипед . Принимая за начало координат вершину , а за базисные векторы , и , найдите координаты:
а) вершин ;
б) точек и – середин ребер и соответственно.

2. Определить, при каком значении a векторы и будут перпендикулярны

3. Установить, образуют ли векторы базис в множестве всех векторов, если .

4. Найти координаты вершин треугольника, если даны уравнения двух сторон треугольника и двух высот:
(АС) х-2у-3=0 6х-12у-18=0
(АВ) х+2у+1=0 2х-у-12=0.

5. Построить кривую .

6. Привести кривую к каноническому виду:

7. Найти точку , симметричную точке М относительно прямой L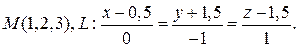

8. Составьте уравнение плоскости, которая проходит через точку перпендикулярно к двум плоскостям: .

9. Составьте уравнение плоскости, проходящей через прямую перпендикулярно к плоскости

10. Докажите параллельность прямых и

11. Составить уравнение сферы, если известны координаты центра и плоскость касается сферы.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 5

1. Дан параллелепипед . Принимая за начало координат вершину , а за базисные векторы , , , найдите координаты:
а) точек и пересечения диагоналей граней и ;
б) точки О пересечения диагоналей параллелепипеда.

2. , . Найдите направляющие косинусы вектора .

3. Найдите площадь параллелограмма, построенного на векторах и , если и - единичные векторы и .

4. Найти уравнения и длины сторон и медиан треугольника если даны две вершины треугольника А(-1, -1), В(9, -6), и точка пересечения медиан М(13/3; -5/3).

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку , симметричную точке М относительно прямой L

8. Определите двугранный угол, образованный пересечением пары плоскостей

9. Вычислите кратчайшее расстояние между прямыми:

10. Составьте уравнения проекции прямой на плоскость .

11. Составить уравнение сферы, если известно, что точки , , , лежат на сфере.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 6

1. В трапеции ABCD известно отношение длин оснований: . Найти координаты вектора в базисе из векторов и .

2. Заданы векторы . Найти :
а)
б)
с) .

3. Даны три вектора Найти координаты вектора в базисе из векторов .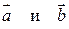

4. Найти уравнения и длины сторон и медиан треугольника, если даны три вершины А(1, 1), В(-9, 6), С(-5, -2).

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L

8. Точка служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.

9. Найти координаты проекции точки М (1,0,1) на плоскость .

10. Докажите, что прямая лежит в плоскости

11. Составить уравнение сферы, если известны координаты центра C(-3;-1;2) и радиус R=3.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями

Вариант 7

1. В тетраэдре ABCD DM – медиана грани BCD и Q – центр масс этой грани. Найти координаты векторов и в базисе ( , , ).

2. Определить координаты точки М, если ее радиус-вектор составляет с координатными осями одинаковые углы и его модуль равен 3.

3. Даны точки A(1, 2, 0), B(0, 1, 4) и С(-1, 1, 1). На плоскости XOZ найти точку D так, чтобы вектор был коллинеарен вектору .

4. Найти вершины, и уравнения медиан треугольника, если даны уравнения трех сторон (АС): х-2у-3=0; (АВ): х+2у+1=0; (ВС): 2х+у+14=0.

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L

8. Укажите значение λ, при котором плоскости : 3x – λy + 3 = 0 и
: x – 2y + 5z – 10 = 0 будут перпендикулярными.

9. Составьте уравнения прямой, образованной пересечением плоскости
Р: -5x + 2y – z + 1 = 0 с плоскостью, проходящей через ось OZ и точку

10. Найдите точки пересечения прямой с координатными плоскостями.

11. Составить уравнение сферы, если известны координаты центра C(-3;2;-1) и точки на сфере M(-2;1;-3).

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями

Вариант 8

1. ABCDEF – правильный шестиугольник, причем = , = . Выразить через и векторы , , , , , , .

2. Найти угол, образованный единичными векторами если известно, что векторы перпендикулярны

3. Найти тупой угол (в радианах) между диагоналями параллелограмма, построенного на векторах .

4. Найти уравнения и длины сторон треугольника, если даны две вершины треугольника А(-1, -1), В(-11, 4) и точка пересечения высот К(-7, -4).

5. Построить кривую

6. Привести кривую к каноническому виду: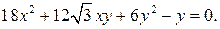

7. Найти точку, симметричную точке М относительно прямой L

8. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям

9. Докажите, что прямая 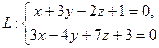пересекает ось OX.

10. Составьте уравнения прямых, образованных пересечением плоскости с координатными плоскостями.

11. Составить уравнение сферы, если известно, что точки (3;-3;2) и (5;3;-6) - концы диаметра сферы.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями

Вариант 9

1. В пространстве заданы треугольники ABC и . M и – точки пересечения их медиан. Выразить через векторы , и

2. Доказать, что вектор перпендикулярен вектору .

3. Найти вектор , коллинеарный вектору , если его проекция на вектор равна 5.

4. Найти координаты вершин треугольника, если даны уравнения двух сторон треугольника и двух высот:
(АС): х-2у+1=0 2х-4у+2=0
(АВ): х+2у-3=0 2х-у-19=0.

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку , симметричную точке М относительно прямой L,если

8. Составьте уравнение плоскости, которая проходит через точку перпендикулярно к двум плоскостям: .

9. Составьте уравнение плоскости, проходящей через прямую перпендикулярно к плоскости

10. Проверить параллельность прямых или найти угол между ними: и

11. Составить уравнение сферы, если известны координаты центра С(1;-4;-1) и плоскость 2x – y + 2z + 2 = 0 касается сферы.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 10

1. Точки E и F – середины сторон AD и BC четырехугольника ABCD. Доказать, что = ( + ).

2. Для заданных векторов вычислить проекцию вектора на вектор .

3. Упростить выражение

4. Найти уравнения и длины сторон и медиан треугольника если даны две вершины треугольника А(-1, 1), В(19, -9), и точка пересечения медиан М(29/3; -1/3).

5. Построить кривую .

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L, если

8. Определите двугранный угол, образованный пересечением пары плоскостей

9. Вычислите кратчайшее расстояние между прямыми:

10. Составьте уравнения проекции прямой на плоскость .

11. Составить уравнение сферы, если известно, что точки лежат на сфере.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 11

1. Дан произвольный треугольник ABC. Доказать, что существует треугольник , стороны которого соответственно равны и параллельны медианам исходного треугольника ABC.

2. Для векторов вычислить проекцию вектора на вектор

3. Проверить, компланарны ли векторы .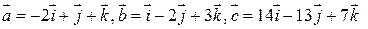

4. Найти уравнения и длины сторон и медиан треугольника, если даны три вершины А(1, -1), В(21, -11), С(13, 5).

5. Построить кривую .

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L,если

8. Точка служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.

9. Найти координаты проекции точки М(0;2;1) на плоскость P: 2x+4y–3=0

10. Докажите, что прямая лежит в плоскости
P:

11. Составить уравнение сферы, если известны координаты центра C(0;-5;3) и радиус R = 5.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 12

1. Используя свойства векторов, доказать, что сумма квадратов медиан треугольника относится к сумме квадратов его сторон как 3 : 4.

2. Найти единичный вектор , параллельный вектору

3. .Проверить, компланарны ли векторы

4. Найти вершины, и уравнения медиан треугольника, если даны уравнения трех сторон (АС): х-2у-1=0; (АВ): х+2у+3=0; (ВС): 2х+у-27=0.

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L, если

8. Укажите значение λ, при котором плоскости : x–y+λz–5 = 0 и : x+z–2=0 будут перпендикулярными.

9. Составьте уравнения прямой, образованной пересечением плоскости с плоскостью, проходящей через ось ОУ и точку .

10. Найдите точки пересечения прямой с координатными плоскостями.

11. Составить уравнение сферы, если известны координаты центра C(2;-1;3) и точки на сфере M(4;1;2).

Найти уравнения линий пересечения данной поверхности с координатными плоскостями Вариант 13

1. AD,BE и CF – медианты треугольника ABC. Доказать равенство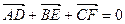

2. .Даны векторы . Вычислить направляющие косинусы вектора

3. При каком значении l векторы будут компланарны, если .

4. Найти уравнения и длины сторон треугольника, если даны две вершины треугольника А(-1, 1), В(-21, 11) и точка пересечения высот К(-13, -5).

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найдите точку, симметричную точке М относительно прямой L, если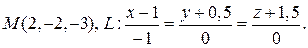

8. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям ,

9. Докажите, что прямая пересекает ось ОХ.

10. Составьте уравнения прямых, образованных пересечением плоскости с координатными плоскостями.

11. Составить уравнение сферы, если известно, что точки и - концы диаметра сферы.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями

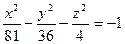
Вариант 14

1. и - медианы треугольника ABC. Выразить через и векторы .

2. Проверить, что точки А(2; 4; 1), В(3; 7; 5), С(4; 10; 9) лежат на одной прямой

3. Вычислить 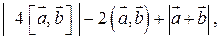где

4. Найти координаты вершин треугольника, если даны уравнения двух сторон треугольника и двух высот:
(АС): х-2у-3=0 х-2у-3=0
(АВ): х+2у+1=0 2х-у+15=0.

5. Построить кривую .

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L, если

8. Составьте уравнение плоскости, которая проходит через точку перпендикулярно к двум плоскостям: .

9. Составьте уравнение плоскости, проходящей через прямую перпендикулярно к плоскости

10. Докажите параллельность прямых и

11. Составить уравнение сферы, если известны координаты центра C(-1;1;3) и плоскость 4x – 3y + 6 = 0 касается сферы.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями

Вариант 15

1. .В параллелограмме ABCD обозначены . Выразить через векторы : , где М - точка пересечения диагоналей параллелограмма.

2. Для заданных векторов вычислить :
а)
б)

3. Даны векторы . В базисе из этих векторов найти координаты вектора .

4. Найти уравнения и длины сторон и медиан треугольника если даны две вершины треугольника А(-1, -1), В(-21, 9), и точка пересечения медиан М(35/3; 1/3).

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно прямой L, если

8. Определите двугранный угол, образованный пересечением пары плоскостей

9. Вычислите кратчайшее расстояние между прямыми:

10. Составьте уравнения проекции прямой 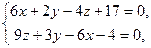на плоскость .

11. Составить уравнение сферы, если известно, что точки, лежат на сфере.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

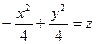Вариант 16

1. В равнобедренной трапеции ОВСА угол ÐВОА=60°, M и N - середины сторон ВС и АС. Выразить векторы через - единичные векторы направлений .

2. Вычислить , если , где .

3. Найти координаты четвертой вершины тетраэдра АВСD, если известно, что она лежит на оси ОУ, а объём тетраэдра равен 2, если А(0;1;1), В(4;3;-3), С(2;-1;1).

4. Найти уравнения и длины сторон и медиан треугольника, если даны три вершины А(1, 2), В(11, -3), С(7, 3).

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно плоскости Р, если

8. Точка служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.

9. Найти проекцию точки М(-1;0-1) на плоскость P: 2x + 6y - 2z +11 = 0

10. Докажите, что прямая лежит в плоскости

11. Составить уравнение сферы, если известны координаты центра C(5;-3;7) и радиус R = 1.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 17

1. В треугольнике ABC проведена биссектриса AD. Найти координаты вектора в базисе, образованном векторами .

2. Даны три вектора : . Вычислить: .

3. Вектор перпендикулярен к векторам , угол между равен 30°. Зная, что , вычислить .

4. Найти вершины, и уравнения медиан треугольника, если даны уравнения трех сторон (АС): х-2у+5=0; (АВ): х+2у - 3=0; (ВС): 2х+у - 15=0.

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно плоскости Р, если

8. Укажите значение λ, при котором плоскости : 5x–λy + 3z = 0 и : 4x–y–z+2=0 будут перпендикулярными.

9. Составьте уравнения прямой, образованной пересечением плоскости с плоскостью, проходящей через ось оy и точку

10. Найдите точки пересечения прямой с координатными плоскостями.

11. Составить уравнение сферы, если известны координаты центра C(-1;5;2) и точки на сфере M(2;2;2).

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 18

1. Даны три точки O, A, B не лежащие на одной прямой. Принимая за базисные векторы и , найти координаты вектора , если точка М лежит на отрезке АВ и .

2. Вычислить работу силы при перемещении материальной точки из положения А(-1; 2; 0) в положение В(2; 1; 3)?

3. Найти проекцию вектора на вектор, составляющий с осью абсцисс угол в 60°, с осью ординат 45°, а с осью аппликат - острый угол.

4. Найти уравнения и длины сторон треугольника, если даны две вершины треугольника А(1, -2), В(11, -7) и точка пересечения высот К(7, 1).

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно плоскости P, если

8. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям

9. Докажите, что прямая пересекает ось OZ.

10. Составьте уравнения прямых, образованных пересечением плоскости с координатными плоскостями.

11. Составить уравнение сферы, если известно, что точки и - концы диаметра сферы.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями

Вариант 19

1. Даны три точки О, А, В не лежащие на одной прямой. Принимая за базисные векторы и , найти координаты вектора , если точка N лежит на прямой АВ вне отрезка АВ и .

2. Пусть векторы ортогональны. При каком значении параметра l вектор ортогонален вектору ?

3. Вычислить высоту параллелепипеда, построенного на трех векторах , если за основание взят параллелограмм, построенный на векторах . Кроме того, известно, что - взаимно перпендикулярные орты.

4. Найти координаты вершин треугольника, если даны уравнения двух сторон треугольника и двух высот:
(АС): х-2у+3=0 2х-4у+6=0
(АВ): х+2у-5=0 2х-у+9=0.

5. Построить кривую .

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно плоскости Р, если

8. Составьте уравнение плоскости, которая проходит через точку перпендикулярно к двум плоскостям: .

9. Составьте уравнение плоскости, проходящей через прямую перпендикулярно к плоскости

10. Найти угол между прямыми 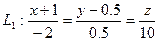и

11. Составить уравнение сферы, если известны координаты центра C(1;0;1) и плоскость касается сферы.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 20

1. Дан правильный шестиугольник OABCDE со стороной ОА = 3. Обозначим , и .Установить зависимость между ними. Выразить через и векторы .

2. Доказать, что если диагонали четырехугольника в точке пересечения делятся пополам, то этот четырехугольник - параллелограмм..

3. Найти длину вектора , если , а угол между векторами равен 60°.

4. Найти уравнения и длины сторон и медиан треугольника если даны две вершины треугольника А(-1, 2), В(-11, 7), и точка пересечения медиан М(19/3;8/3).

5. Построить кривую .

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно плоскости Р, если

8. Найти угол между плоскостями

9. Вычислите кратчайшее расстояние между прямыми:

10. Составьте уравнения проекции прямой на плоскость .

11. Составить уравнение сферы, если известно, что точки лежат на сфере.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 21

1. Вне плоскости параллелограмма ABCD взята точка О. В базисе из векторов найти координаты вектора , где К – середина стороны AD.

2. Найти направляющие косинусы вектора

3. Составляют ли векторы ортогональный базис трехмерного пространства?

4. Найти уравнения и длины сторон и медиан треугольника, если даны три вершины А(1; -2), В(-9; 3), С(-5; -5).

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно плоскости Р, если

8. Точка служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.

9. Найти проекцию точки М(2;1;0) на плоскость P: y + z + 2 = 0.

10. Докажите, что прямая лежит в плоскости

11. Составить уравнение сферы, если известны координаты центра C(1;-2;0) и радиус R = 3.

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 22

1. В плоскости треугольника АВС найти точку О такую, что . Существуют ли такие точки вне плоскости треугольника?

2. Векторы неколлинеарны. При каких значениях скаляра l коллинеарны векторы ?

3. .Образуют ли базис в пространстве векторы {1; 0; 0} , ? Будет ли он ортонормированным?

4. Найти вершины, и уравнения медиан треугольника, если даны уравнения трех сторон (АС): х-2у-3=0; (АВ): х+2у+5=0; (ВС): 2х+у+19=0.

5. Построить кривую

6. Привести кривую к каноническому виду:

7. Найти точку, симметричную точке М относительно плоскости Р, если

8. Укажите значение λ, при котором плоскости : λx – 3y + 2z + 5 = 0 и
: 3x + 3y - 3z - 8 = 0 будут перпендикулярными.

9. Составьте уравнения прямой, образованной пересечением плоскости с плоскостью, проходящей через ось ОХ и точку

10. Найдите точки пересечения прямой с координатными плоскостями.

11. Составить уравнение сферы, если известны координаты центра C(2;-1;3) и точки на сфере M(0;1;2).

12. Найти уравнения линий пересечения данной поверхности с координатными плоскостями
.

Вариант 23

1. Даны 3 точки не лежащие на одной прямой. Найти координаты точки пересечения медиан треугольника АВС.

2. . Найти направляющие косинусы вектора .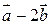

3. Вычислить: 1) ;
2) .

4. Найти уравнения и длины сторон треугольника, если даны две вершины треугольника А(1; 2), В(21; -8) и точка пересечения высот К(13; 8).

5. Построить кривую

6. Привести кривую к каноническому виду: .

7. Найти точку, симметричную точке М относительно плоскости Р, если

8. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям

9. Докажите, что прямая пересекает ось ОУ.

10. Составьте уравнения прямых, образованных пересечением плоскости с координатными плоскостями.

11. Составить уравнение сферы, если известно, что точки и - концы диаметр