Примечание 1.

Эллипс.

Определение: Эллипсом называется геометрическое место точек плоскости, для которых, сумма расстояний до 2-х фиксированных этой же плоскости, называемых фокусами эллипса, есть величина постоянная (= 2а).

Вывод уравнения эллипса.

Выберем систему координат следующим образом:

И F_1,F₂ – фокусы эллипса,

т. эллипсу.

F_1,F₂ – расстояние между фокусами эллипса.

Очевидно, что , так как 2a – сумма 2-х сторон 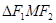, а 2с – его третья сторона.

Таким образом, по определению эллипса имеем:

(1)

Запишем это уравнение в координатной форме, заменив и , получим уравнение эллипса в данной системе координат:

(2)

Упростим его:

;

Разделим на:

Получим: (3)

Так как , то можно обозначить (4), то есть имеем простейшее (каноническое) уравнение эллипса:

(5)

Примечание 1.

Вообще говоря, надо доказать, что уравнение (5) есть уравнение данного эллипса, так как это уравнение получено из уравнения (2) двукратным освобождением от радикалов, очевидно лишь, что уравнение (5) есть следствие уравнения (2). Мы должны доказать, что уравнение (2) есть в свою очередь следствие уравнения (5), т.е. , что они эквивалентны.

Доказательство смотрите в учебнике Н. В. Ефимова (Краткий курс аналитической геометрии, М, 2005, стр. 72 (2-ой абзац сверху)- стр. 73) или в другом курсе аналитической геометрии.

Таким образом, уравнение (5):

Определяющее эллипс в некоторой системе координат декартовых прямоугольных, есть уравнение 2-ой степени относительно “x” и “y”.

Форма эллипса:

2)

То есть

Таким образом, эллипс целиком лежит внутри прямоугольника, определяемого этими неравенствами.

3)Уравнение сохраняет вид, если “x” заменить на “-x”, а “y” заменить на “-y”.

Таким образом, оси координат x=0 ( ось OY ) и y=0 ( ось OX ) являются осями симметрии эллипса, следовательно, достаточно построить дугу эллипса, лежащую в первой четверти.

4)Построим эллипс в 1-ой четверти. Имеем - уравнение эллипса для первой четверти, при этом .

Или после преобразования , .

Имеем при

При

Замечаем, что при возрастании “x” от “0” до ”a”, “y” убывает от “0” до ”b”.

Строи кривую в 1-ой четверти.

5)Строим эллипс.

Точки М₁, М₂, М₃, М₄ – вершины эллипса.

-большая ось (a – большая полуось).

-малая ось (b – малая полуось).

Так как . Точка пересечения осей симметрии называется центром эллипса (т. ).

c-половина фокусного расстояния.

Имеем:

Замечание 1: при эллипс превращается в окружность радиуса и с центром в начале координат.

Эксцентриситет эллипса.

Для характеристики формы эллипса пользуются эксцентриситетом .

Определение: Эксцентриситетом эллипсаназывается отношение половины фокусного расстояния к большой полуоси, т.е.

(6)

Т.к. , то

.

Чем ближе к единице, тем меньше, следовательно, отношение , тем более эллипс вытянут вдоль оси OX. При , , следовательно, и эллипс превращается в сдвоенную большую ось. Чем больше , тем больше форма эллипса приближается к окружности.

При , имеем окружность , т.е. для окружности .

Замечание 2.

Рассмотрим уравнение эллипса , где , т.е. b - большая полуось, a – малая полуось. Для него .

Примеры.

1)Построить кривую по уравнению и вычислить c, , построить фокусы

Решение:

, имеем:

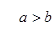
У этого эллипса центр находится в точке

2)Написать уравнение эллипса, для которого большая полуось , центр лежит в точке и оси координат являются осями симметрии эллипса. Построить эллипс.

Решение:

Если , то , следовательно Получим уравнение эллипса: .

Гипербола.

Определение:Гиперболойназывается геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек этой же плоскости, называемых фокусами гиперболы, есть величина постоянная.

Вывод уравнения гиперболы.

Выберем прямоугольную систему координат OXY так, чтобы центр гиперболы находился в начале координат, а фокусы располагались на оси абсцисс.

F₁,F₂ – фокусы гиперболы

Т. M (x;y) принадлежит гиперболе

F₁, F₂=2c – расстояние между фокусами гиперболы

a<c, т.к. 2a – разность двух сторон треугольника F₁MF₂, а 2с – это его третья сторона

Таким образом по определению гиперболы имеем:

Объединив (7) и (8) имеем:

Это и есть уравнением гиперболы в данной системе координат. Получим уравнение гиперболы в более простом виде, рассуждая аналогично пункту (1)

Имеем:

Возведя обе части в квадрат, получим:

Здесь , умножим обе части последнего уравнения на (-1), получим:

;

Здесь , разделим обе части уравнения на , получим:

обозначив, , получим каноническое уравнение гиперболы

Примечание 3:

Оно аналогично примечанию 1, смотри Н. В. Ефимов (краткий курс аналитической геометрии, М, 2005, стр. 83-84).

Таким образом уравнение (12) , определяющее гиперболу в некоторой системе декартовых прямоугольных координат, есть уравнение 2-ой степени относительно “x” и “y”.

Форма гиперболы

1) , т.е.

2) Аналогично рассуждая(смотрите пунтк1(2) ) получим, что оси координат x=0 и y=0 – оси симметрии гиперболы, следовательно достаточно построить гиперболу в I – четверти. Точка пересечения осей симметрии т. О(0;0) называется центром гиперболы.

3) Построим гиперболу для I-четверти. Для I-ой четверти уравнение гиперболы , для

Или после преобразования , для .

При , таким образом т. гиперболе.

При возрастании “x”, возрастает “y”, причём “y” стремится к , так как разность между ординатами прямой и гиперболы имеет вид:

если “x” неограниченно возрастает и геометрически гипербола в I-ой четверти неограниченно приближается к прямой , называемой асимптотой гиперболы.

Примечание 4: Строгое доказательство существования 2-х асимптот основано на приложении производной к исследованию и построению графиков функций.

Строим гиперболу в I четверти:

4) Строим гиперболу , используя пункты 3(1) – 3(4).

Точки и - называются вершинами гиперболы.

Та ось, с которой у гиперболы есть пересечения и на которой лежат её вершины, называется действительной осью(в нашем случае ось ОХ). Ось OY – мнимая ось.

Замечание: Таким образом для построения гиперболы необходимо:

1. От центра симметрии гиперболы (т. О(0;0) ) отложить по оси ОХ вправо и влево по “a”, а по оси OY вверх и вниз по ”b”, то есть построить прямоугольник с центром в т. О(0;0) и со сторонами 2a и 2b.
2. Провести диагонали прямоугольника и продолжить их (получим асимптоты гиперболы).
3. Правильно расположить вершины гиперболы. Они всегда лежат на действительной оси. Это видно из уравнения: . Знак “-” перед указывает на то, что ось симметрии – ось OY(х=0) – мнимая ось.

Знак “+” перед указывает на то, что ось симметрии - ось ОХ (y=0) – действительная ось.

Эксцентриситет гиперболы

Он служит для характеристики формы гиперболы.

Определение: Эксцентриситетом гиперболы называется отношение половины фокусного расстояния к действительной полуоси, т. е , где , для гиперболы .

Чем меньше эксцентриситет, то есть чем ближе он к “1”, тем меньше , тем меньше, следовательно, отношение ,значит, более вытянут её прямоугольник в направлении оси, соединяющей вершины гиперболы.

Замечание:

1. если a=b, то имеем гиперболу или , которая называется равноостной гиперболой.

2. Определение: Гиперболы и называются сопряжёнными гиперболами.

Построим сопряжённые гиперболы.

Эксцентриситет гиперболы равен ,

Примеры.

1) Построить кривую по уравнению и вычислить с, , указать фокусы:

Решение: Уданной гиперболы a=4 - мнимая полуось, b=3 – действительная полуось и . Таким образом .

2) Написать уравнение гиперболы для которой a=3 (действительная полуось), , центр лежит в О(0;0), построить эту гиперболу с фокусами.

Решение: (мнимая полуось). (равноосная гипербола).

Парабола

Определение: Параболой называется геометрическое место точек плоскости равноудалённых от данной точки, называемой фокусом и от данной прямой, называемой директрисой, расположенных на этой плоскости.

Вывод уравнения параболы.

В прямоугольной декартовой системе координат расположим директрису и фокус следующим образом:

p>0.

“p”-расстояние от фокуса до директрисы.

- уравнение директрисы параболы, -фокус параболы, точка параболе.

По определению параболы имеем: MF=MB (1)

Заменим Получим уравнение параболы в этой системе координат: (2), упростим его:

Примечание 1: Надо доказать что уравнение (3) есть уравнение данной параболы. Доказательство смотрите в учебнике Н. В. Ефимова (краткий курс аналитической геометрии, М. 2005, стр. 96).

Таким образом уравнение -простейшее, т.е. каноническое уравнение параболы, определяющее параболу в некоторой системе декартовых координат, есть уравнение 2-ой степени, относительно “y”.

Форма параболы

1) , т.е. парабола лежит справа от оси OY(х=0)

2) Так как , то ось ОХ(y=0) – ось симметрии параболы.

3) При т.е.О(0;0) параболе и называется вершиной параболы.

4) При неограниченном возрастании “x” неограниченно возрастает и ”y”: .

Замечание 1:

1) Направление параболы в точке О(0;0) перпендикулярно к оси ОХ;

2) Часть параболы, лежащая в верхней полуплоскости, своей выпуклостью обращена “вверх”.

Не будем доказывать эти свойства, т.к. такого рода исследование линии наиболее естественно проводить средствами математического анализа.

Виды парабол.

Уравнение (p>0) сводится к уравнению путём замены “x” на “-x”, т.е. путём преобразования координат, которое соответствует изменению оси OX на противоположное. Отсюда следует, что уравнение также определяет параболу, ось которой совмещена с осью OX, а вершина – с началом координат, но котонная расположена в левой полуплоскости ( ).

Замечание 2:

1) Осью симметрии любой параболы является та ось, одноимённая координата которой входит в 1-ой степени . Или так: если переменная “y” в уравнении параболы входит в чётной степени, то график симметричен относительно оси ОХ(y=0).

, здесь “х” – в 1-ой степени и, следовательно, осью симметрии является ось ОХ(y=0).

2) Знак “+” в уравнениях и , (p>0), перед (2px) и (2py) указывает на то, что ветви параболы направлены в положительном направлении оси симметрии.

Знак “-” перед (2px) и (2py) указывает на то что, ветви параболы направлены в отрицательном направлении оси симметрии.

Это имеет место, так как , следовательно, ;

, следовательно, ;

, следовательно, ;

Пример.

Построить кривую по уравнению, её директрису, фокус:

Решение: Имеем , следовательно, .

Ось симметрии – ОХ(y=0). Ветви параболы направлены в отрицательном направлнеии оси ОХ. Т. О(0;0) – вершина параболы. -фокус параболы.

Эллипс, гипербола и парабола с осями симметрии параллельными осям координат.

1) Параллельный перенос осей координат:

Связь

Переход от старых( ) координат к новым( )/

2) Пусть имеем эллипс с осями симметрии, параллельными осям координат в т. и с полуосями a; b.

С осями симметрии эллипса совместим новые оси и , которые параллельны соответственно осям OX и OY. Имеем 3(1).

в , заменив , где ,

получим в XOY:

Это и есть уравнение эллипса с осями симметрии параллельными осям координат.

3) Рассуждая аналогично пункту 2), получим уравнения гипербол с осями симметрии параллельными осям координат:

4) Для параболы с осями симметрии параллельными осям координат имеем:

4.Примеры:

По чертежу запишите уравнение кривых:

1)

Решение:

1. Это парабола.

2. Ось симметрии её x=5(прямая параллельная оси OY), поэтому “y” входит в уравнение в 1-ой степени.

3. Вершина параболы лежит в точке .

4. Ветви параболы направлены в положительном направлении оси симметрии.

5. Таким образом имеем уравнение кривой:

6. Находим (2p), зная, что точка параболе, следовательно, её координаты удовлетворяют уравнению параболы:

Таким образом:

2)

Решение:

1. Это гипербола.

2. Оси симметрии x=4 и y=7(мнимая).

3. Центр лежит в т. .

4. Полуоси: a=5; b=5

Таким образом имеем уравнение:

;

3)

Решение

1. Это эллипс.

2. оси симметрии: y=0; x=1.

3. Центр лежит в т. .

4. Большая полуось a=3, малая b=2

Таким образом имеем уравнение: ,

4) По уравнениям построить кривые:

1.

2.

3.

4.

Решения:

1. Это гипербола.

(мнимая)

2. Это окружность

3. Это парабола.

1. -ось симметрии.

Чтобы найти точки пересечения параболы с осью надо решить систему: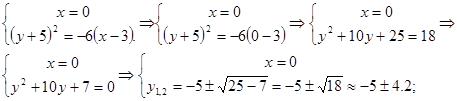

Таким образом

2. Находим точки пересечения с осью OX:

Таким образом

4. Это эллипс.

Общее уравнение кривой II порядка.

Если в уравнениях кривых: эллипса, гиперболы и параболы, с осями симметрии параллельными осям координат раскрыть скобки, то все они могут быть приведены к пятичленному уравнению 2-го порядка, которое имеет вид:

(1)

И называется общим уравнением кривой 2-го порядка.

Проанализировав отличие друг от друга уравнений вида (1) для эллипса, гиперболы и параболы, можно увидеть, что в случае эллипса - знаки коэффициентов A и C одинаковы, в случае гиперболы - знаки коэффициентов A и C различны, и в случае параболы один из квадратов отсутствует, что влечёт за собой равенство нулю соответствующего коэффициента A или C (одновременно A и C нулю равны быть не могут, иначе получается уравнение 1-го порядка, т.е. уравнение прямой).

Таким образом, произведение AC определяет кривую, уравнение которой имеет вид (1).

Для эллипса AC>0;

Для гиперболы AC<0;

Для параболы AC=0;

Рассмотрим обратную задачу.

В декартовой прямоугольной системе координат дано уравнение:

(1)

Для построения кривой и полного представления о том, как она расположена на плоскости, необходимо привести уравнение (1) к каноническому виду, т.е. выделить полные квадраты в этом уравнении.

Например, приведём уравнение к каноническому виду.

Решение:

В декартовой прямоугольной системе координат уравнение 2-го порядка:

, может соответствовать следующим семи типам линий второго порядка : эллипсы, гиперболы, параболы, пары пересекающихся прямых, точки, пары параллельных прямых, пары совпадающих прямых.

Примеры.

1. Какое геометрическое место точек задано уравнением

?

Решение:

Так как правая часть уравнения не положительна, то и , следовательно, это уравнение равносильно системе :

- это множество точек эллипса, у которых , т.е. нижняя половина эллипса.

2. По данному уравнению определите тип кривой. Приведите уравнение к каноническому виду, постройте кривую на плоскости XOY. Найдите координаты фокусов. Составьте уравнения асимптот для гиперболы:

1)

2)

3)

4)

Решение:

1)

См. таблицу(1). Дано уравнение кривой гиперболического типа.

Приводим уравнение к каноническому виду.

- каноническое уравнение гиперболы.

- центр симметрии кривой;

Уравнения асимптот:

2)

Дано уравнение кривой параболического типа.

Приводим уравнение к каноническому виду.

- каноническое уравнение параболы.

- вершина параболы.

Найдём точки пересечения параболы с осью OY:

x=0, тогда ; 16y=25 или т.е.

Координаты фокуса:

или

Уравнение директрисы:

или

3)

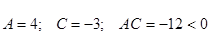
Дано уравнение гиперболического типа. Приводим его к каноническому виду.

Это случай вырождения гиперболы в 2 пересекающиеся прямые:

точка пересечения прямых т.

Угловые коэффициенты прямых:

Имеем эти прямые:

и

4)

Дано уравнение кривой эллиптического типа.

Приводим к каноническому виду.

Это случай вырождения эллипса в точку

Данному удовлетворяют координаты только одной точки:

3. Построить кривую, заданную уравнением

Это уравнение равносильно системе: или , следовательно, в условии было дано уравнение части гиперболы , для которой ;

Строим только правую ветвь гиперболы, т.к. именно она располагается в той полуплоскости, где . Уравнение асимптот

4. Построить кривую, заданную уравнением

Решение:

Это уравнение части некоторой кривой, и оно равносильно следующей системе:

Следовательно, в условии дано уравнение той части эллипса

, которая лежит в полуплоскости

Литература.

1. С. В. Фролов, Р. Я. Шостак «Курс высшей математики», М. изд-во «Высшая школа», 1966г.

2. А. Н. Канатников, А. П. Крищёнко «Аналитическая геометрия», М. изд-во МГТУ им. Н. Э. Баумана, 1999 г.

3. Н. В. Ефимов «Краткий курс аналитической геометрии», М. Физматлит, 2005г.

4. В. А. Ильин, Э. Г. Позняк «Аналитическая геометрия» М. Физматлит, 2003г.