
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример решения.
Федеральное агентство по образованию Российской Федерации
Филиал «СЕВМАШВТУЗ» государственного образовательного учреждения высшего профессионального образования «Санкт-Петербургский государственный морской технический университет» в г. Северодвинске
Курзанова Е. В.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Методические указания к выполнению расчетно-графической работы по кинематике
Северодвинск
УДК-531
Теоретическая механика: Методические указания к выполнению расчетно-графической работы по кинематике./Сост. Е. В. Курзанова – Северодвинск: РИО Севмашвтуза, 2007 – 16с.
Методические указания предназначены для студентов всех специальностей, изучающих курс «Теоретическая механика». Методические указания по теоретической механике раздел “Кинематика” разработаны для выполнения расчетно-графической работы по теме: «Прямолинейное и криволинейное движение точки».
Указания содержат основные положения рассматриваемой темы, план решения расчетно-графической работы, таблицу с заданиями, пример решения.
Рецензенты: старший преподаватель Л.А. Ковалёв
к.т.н., доцент Д.В. Кузьмин
ведущий специалист НИТИЦ ФГУП
«ПО «СЕВМАШ» Ю.П. Голованов
Печатается по решению редакционно-издательского совета Севмашвтуза.
© СЕВМАШВТУЗ, 2007 г.
СОДЕРЖАНИЕ
Основные понятия раздела «Кинематика точки». 5
1. Содержание задания. 6
1.1. План выполнения задания. 6
1.2. Таблица с исходными данными. 8
1.3. Пример решения. 10
1.4. Вопросы для защиты расчётно-графической работы: “Кинематика точки”. 12
СПИСОК ЛИТЕРАТУРЫ... 15
ПРЕДИСЛОВИЕ
Методические указания к выполнению расчетно-графической работы содержат основные теоретические понятия раздела кинематика точки.
В методических указаниях содержатся план решения задания, таблица с заданиями, пример решения.
Целью методических указаний является оказание помощи студентам при решении задач по разделу теоретической механики: «Кинематика точки».
Методические указания предназначены для студентов всех специальностей, изучающих курс «Теоретическая механика».
Основные понятия раздела «Кинематика точки».
Тема: Кинематика точки. Прямолинейное и криволинейное движение
точки.
Кинематика – раздел теоретической механики, изучающий законы механического движения с геометрической точки зрения (без учета действующих сил и существующих масс).
Основная задача кинематики – уметь устанавливать вид траектории, находить кинематические характеристики (скорость, ускорение).
Траектория точки – это линия по которой движется точка. Траектория может быть прямолинейной или криволинейной. Вид траектории зависит от выбранной системы отсчёта и от характера движения.
Существует три способа задания движения:
1. Радиус-векторный
 .
.
2. Координатный:
 ;
;  ;
;  .
.
3. Естественный.
 .
.
Скорость характеризует быстроту движения, ускорение характеризует быстроту изменения скорости.
В задании К-1 необходимо по заданным в координатной форме уравнениям движения точки установить вид траектории и определить значения скорости и ускорений (полное, касательное, нормальное).
Задача должна быть решена аналитически и графически.
Содержание задания.
По заданным уравнениям движения точки  установить вид её траектории и для момента времени
установить вид её траектории и для момента времени  найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке.
найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке.
План выполнения задания.
1. Установить вид траектории по заданным уравнениям движения.
Если в одном уравнении существует линейная зависимость от времени, то необходимо исключить время из этого уравнения. Найденное значение t нужно подставить в оставленное уравнение  или
или  и получить зависимость
и получить зависимость  или
или 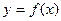 .
.
Далее необходимо в выбранном масштабе построить график траектории (задавая значения y получить значения x или наоборот).
Если зависимость x(t) и y(t) тригонометрическая (например  ;
;  ), то уравнения приводятся к следующему виду:
), то уравнения приводятся к следующему виду:  или
или  .
.
Получаем уравнение окружности с центром в начале декартовой системы координат (без смещения), радиус окружности R=7 см.
При наличии свободных членов в уравнении, например:
 ;
; 
уравнение можно привести к следующему виду:
 .
.
Получаем уравнение окружности с центром в точке О (5; -4) – IV четверть декартовой системы координат, радиусом R=7 см – уравнение окружности со смещением.
Если после преобразований получится уравнение вида:  - уравнение эллипса с центром в начале координат. Точки пересечения с осью
- уравнение эллипса с центром в начале координат. Точки пересечения с осью  ; с осью
; с осью  . Таким образом, после возможных преобразований и упрощений траектории должны приводиться к следующему виду: парабола, прямая, гипербола, окружность, окружность со смещением, эллипс, эллипс со смещением.
. Таким образом, после возможных преобразований и упрощений траектории должны приводиться к следующему виду: парабола, прямая, гипербола, окружность, окружность со смещением, эллипс, эллипс со смещением.
2. Найти положение точки М на траектории. Для этого нужно подставить заданное значение  в уравнение
в уравнение  и
и 
Дифференцируя x=f(t) по времени, находим значение  - скорость, как проекцию на ось ОХ:
- скорость, как проекцию на ось ОХ:

Найти значение  при заданном значении
при заданном значении  , построить из точки М как вектор.
, построить из точки М как вектор.
Находим значение  - ускорение как проекцию на ось ОХ:
- ускорение как проекцию на ось ОХ:

 ;
;

Найти значение 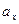 при заданном значении t построить из точки М как вектор.
при заданном значении t построить из точки М как вектор.
3. Найти и построить значения  ;
;  .
.
4. Найти и построить значения скорости  .
.
Скорость должна быть направлена по касательной к траектории, исходящей из точки М.
5. Найти и построить значения касательного (тангенциального) ускорения  по следующей формуле:
по следующей формуле:
 .
.
Если  >0, то вектор
>0, то вектор  совпадает с вектором
совпадает с вектором  , если
, если  <0, то вектор
<0, то вектор  направлен в противоположную сторону вектора
направлен в противоположную сторону вектора  .
.
6. Вычислить значение полного ускорения  . Построить полное ускорение a, как диагональ параллелограмма, построенного на векторах
. Построить полное ускорение a, как диагональ параллелограмма, построенного на векторах  и
и  .
.
7. Вычислить значение нормального ускорения
 .
.
Построить вектор  как перпендикуляр к вектору
как перпендикуляр к вектору  или
или  , исходящий из точки М.
, исходящий из точки М.
В случае уравнения траектории в виде окружности  - центростремительное ускорение, должно пройти через центр окружности.
- центростремительное ускорение, должно пройти через центр окружности.
В случае уравнения траектории имеющего вид прямой  - отсутствует.
- отсутствует.
8. Построить полное уравнение a, как диагональ параллелограмма, построенного на векторах  и
и  . Оно должно совпасть со значением a, найденного из пункта 7 плана.
. Оно должно совпасть со значением a, найденного из пункта 7 плана.
9. Вычислить значение радиуса кривизны траектории  по формуле
по формуле  .
.
Если уравнение траектории окружность, то  .
.
Если уравнение траектории прямая, то  стремится к бесконечности.
стремится к бесконечности.
Таблица с исходными данными.
Задание 1.
По заданным уравнениям движения точки М установить вид её траектории и для момента времени t=t1 (сек) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорение, а также радиус кривизны траектории в соответствующей точке.
Необходимые для решении данные приведены в Таблице 1.
Таблица 1.
| Номер варианта | Уравнения движения | t1, сек | |
| x=x(t), см | y=y(t), см | ||

| 
| 
| |

| 
| ||

| 
| ||

| 
| ||

| 
| ||
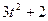
| 
| 
| |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| 
| |

| 
| ||

| 
| ||

| 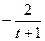
| ||
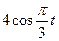
| 
| ||

| 
| 
| |

| 
| ||

| 
| ||

| 
| ||

| 
| 0 
| |

| 
| ||

| 
| 
| |

| 
| ||
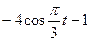
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Пример решения.
Исходные данные в см и сек:
 x=4t
x=4t
y=16t2-1
Решение
Уравнения движения (1) являются параметрическими уравнениями траектории точки М. Чтобы получить уравнения траектории в обычной координатной форме, исключим время t из уравнений движения.
Тогда
|
y=x2-1
Это выражение есть уравнение параболы.
Для определения скорости точки находим проекции скорости на оси координат:
 см/сек;
см/сек;
 см/сек.
см/сек.
Модуль скорости точки
|

Аналогично проекции ускорения точки
 ;
;  см/сек2.
см/сек2.
Модуль ускорения точки
 =32 см/сек2.
=32 см/сек2.
Координаты точки, а также её скорость, ускорение и их проекции на координатные точки для заданного момента времени t=1/2 сек приведены в таблице 2.
Таблица 2.
| Координаты, см | Скорость, см/сек | Ускорение, см/сек2 | Радиус кривизны, см | |||||||
| x | y | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 16.5 | 7.94 | 34.3 |
Касательное ускорение находим путём дифференцирования модуля скорости (3):

 ,
,
При t=1/2 сек
 см/сек2.
см/сек2.
Следовательно, модуль касательного ускорения

 см/сек2.
см/сек2.
Знак “+” при  показывает, что движение точки ускоренное и, следовательно, направление
показывает, что движение точки ускоренное и, следовательно, направление 
 и
и  совпадают.
совпадают.
Нормальное ускорение точки в данные момент времени
 см/сек2.
см/сек2.
Радиус кривизны траектории в той точке, где при t=1/2 сек находиться точка М,
 см.
см.
Полученные значения  ,
,  и
и  также приведены в таблице 2.
также приведены в таблице 2.
Пользуясь уравнением (2), вычерчиваем траекторию (Рис. 1) и показываем на ней положение точки М в заданный момент времени. Вектор  строим по составляющим
строим по составляющим  и
и  , причём этот вектор должен быть направлен по касательной к траектории точки. Вектор
, причём этот вектор должен быть направлен по касательной к траектории точки. Вектор  находим как по составляющим
находим как по составляющим  и
и  , так и по
, так и по  и
и  , чем контролируется правильность вычислений.
, чем контролируется правильность вычислений.
1.4. Вопросы для защиты расчётно-графической работы: “Кинематика точки”.
Вариант 1.
1. Что показывает   ? ?
| а) изменение скорости в единицу длины б) изменение расстояния в единицу времени |
2. Что характеризует  ? ?
| а) изменение  по величине
б) изменение по величине
б) изменение  по направлению по направлению
|
3. Как направлены  и и  в равноускоренном прямолинейном движении? в равноускоренном прямолинейном движении?
| 
|
4. Как направлены  , ,  и и  в равнозамедленном криволинейном движении? в равнозамедленном криволинейном движении?
| 
|
| 5. Какое движение называется равномерным? | а)  б)
б) 
|
| 6. Какие графики соответствуют равнозамедленному движению? | 
|
| 7. Какие уравнения соответствуют равномерному движению? | а)  б)
б)  в)
в) 
|
| 8. Тело движется равномерно по криволинейной траектории. Какие равенства соответствуют этому движению? | а)  ; ;  б)
б)  ; ; 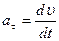 в)
в)  ; ;  г)
г)  ; ; 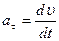
|
Вариант 2.
1. Что показывает   ? ?
| а) изменение скорости в единицу длины б) изменение расстояния в единицу времени |
2. Что характеризует  ? ?
| а) изменение  по величине
б) изменение по величине
б) изменение  по направлению по направлению
|
3. Как направлены  и и  в равнозамедленном прямолинейном движении? в равнозамедленном прямолинейном движении?
| 
|
4. Как направлены  , ,  и и  в равноускоренном криволинейном движении? в равноускоренном криволинейном движении?
| 
|
| 5. Какое движение называется равнопеременным? | а)  б)
б) 
|
| 6. Какие графики соответствуют равноускоренному движению? | 
|
| 7. Какие уравнения соответствуют равноускоренному движению? | а)  б)
б)  в)
в) 
|
| 8. Тело движется равномерно по прямолинейной траектории. Какие равенства соответствуют этому движению? | а)  ; ;  б)
б)  ; ; 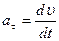 в)
в)  ; ; 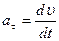 г)
г)  ; ; 
|
СПИСОК ЛИТЕРАТУРЫ
1. Яблонский А.А. Сборник заданий по теоретической механике.- М. Высшая школа, 1985.-366с.
2. Тарг С.М. Краткий курс теоретической механики.- М.: Высшая школа, 1986.-415с.
3. Добронравов В.В. Курс теоретической механики.- М.: Высшая школа, 1974.-526с.
Теоретическая механика:
Методические указания к выполнению
Расчетно-графических работ по
кинематике.
Составитель:
Курзанова Елена Викторовна
Компьютерный набор, верстка автора
Подготка к печати О. А. Мартиросян
Сдано в производство 04.07 г. Подписано в печать 04.08 г.
Уч.-изд. Л.0,31.Формат 84х1081/16. Усл.-печ. Л. 1.68
Изд. №720. Заказ № 697.
Редакционно-издательский отдел Севмашвтуза
164500, г. Северодвинск, ул. Воронина, д.6
Дата добавления: 2015-04-15; просмотров: 307; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Приложение 3 | | | ПЬЯНСТВО И АЛКОГОЛИЗМ |