
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематика. Кинематика- Это раздел теоретической механики, в котором изучается движения материальных объектов с геометрической точки зрения
Вопрос№1
Кинематика- Это раздел теоретической механики, в котором изучается движения материальных объектов с геометрической точки зрения, т.е. без учета действия на них сил.
2е основные задачи:
1. Найти способы задания движения точкиилитела
2. Найти методы определения кинетических характеристик точки или точек твердого тела
Есть три способа описания движения материальной точки:
1. Векторный (Положение точки в пространстве задается с помощью радиус-вектора отложенного в некоторой неподвижной точке)
2. Координатный. (Положение точки в пространстве однозначно определяется заданием ее координат)
3. Естественный. Этот способ используется, когда траектория движения известна заранее (в общем случае это криволинейная траектория). При движении по ней вводят понятие нормальной и тангенциальной составляющей.
Вопрос №2
Коорд

векторный

Направление вектора скорости определяется тремя направляющими косинусами:

|
Вопрос №3
Скорость точки при естественном способе задания движения. За время ∆t точка М по траектории перешла в точку М1. За это время дуговая координата изменилась на ∆S, а радиус-вектор на ∆r.  ,
,  ,
, 
Годограф скоростей в общем случае представляет собой диаграмму ( график), в которой векторы скоростей перемещения точек деформируемого тела отображаются по величине и направлению прямолинейными отрезками ( лучами), исходящими из выбранной на графике произвольной точки, называемой полюсом.
Вопрос№4
 Определение ускорения при векторном способе задания: Определение ускорения при векторном способе задания:
|
 Определение ускорения при координатном способе задания:
Определение ускорения при координатном способе задания: 
Проекциями вектора ускорения на оси координат: 

|
Направляющие косинусы, определяющие направление вектора ускорения в системе координат, будут равны 
Вопрос №5
 Естественный трехгранник (естественные оси координат). Естественным трехгранником называется подвижная прямоугольная система координат, двигающаяся с точкой по траектории. Две оси этой системы координат направлены по единичным векторам касательной и главной нормали к траектории τ и n, а третья ось направлена по вектору b, равному
Естественный трехгранник (естественные оси координат). Естественным трехгранником называется подвижная прямоугольная система координат, двигающаяся с точкой по траектории. Две оси этой системы координат направлены по единичным векторам касательной и главной нормали к траектории τ и n, а третья ось направлена по вектору b, равному  , который называется единичным вектором бинормали к траектории (рис. 65).
, который называется единичным вектором бинормали к траектории (рис. 65).
Вопрос№6
 На рис. 64 показано разложение вектора ускорения a на составляющие aτ и an, когда s'' < 0 . Там же показан вектор скорости V , когда s' > 0.
На рис. 64 показано разложение вектора ускорения a на составляющие aτ и an, когда s'' < 0 . Там же показан вектор скорости V , когда s' > 0.
Отметим, что касательное ускорение можно найти, раскрывая скалярное произведение векторов скорости и ускорения. Произведение равно  откуда
откуда 
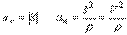
| |
Вопрос№7

При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении можно спроектировать на ось OX и рассматривать их проекции как алгебраические величины.
Вопрос №8
Поступательным движением тела называется такое движение твердого тела, при котором любая прямая проведенная в теле остается во всем времени движения остается параллельной самой себе.
Все точки твердого тела совершающего поступательное движение описывают одинаковые совпадающие при наложении траектории и в любой момент времени имеют геометрически равные скорости и ускорения.
Вопрос №9
Вращательным движениям называется такое движение, при котором все точки принадлежащие некоторой прямой неизменно связной с телом остаются неподвижными в рассматриваемой системе отсчета. Эта неподвижная прямая называется осью вращения. движения
Уравнение движения 
Угловая скорость характеризует быстроту и направление изменения угла поворота в данный момент времени. Величина угловой скорости = 1ой производной от угла поворота по времени. 
Угловое ускорение характеризует быстроту и направление изменения угловой скорости в данный момент времени. Величина углового ускорения = 2ой производной от угла поворота по времени.
Вопрос №10
Линейная скорость точки

 В векторном виде формулу для линейной скорости можно написать как векторное произведение:
В векторном виде формулу для линейной скорости можно написать как векторное произведение:

а ускорение это вторая производная от скорости:
Тангенциальная составляющая ускорения aτ=dv/dt , v = ωR и

Нормальная составляющая ускорения

Вопрос №11
Вектор угловой скорости  направлен по оси вращения тела в ту сторону, откуда вращение тела в данный момент времени видно против хода часовой стрелки. По модулю этот вектор равен абсолютному значению
направлен по оси вращения тела в ту сторону, откуда вращение тела в данный момент времени видно против хода часовой стрелки. По модулю этот вектор равен абсолютному значению  . В качестве точки приложения вектора угловой скорости
. В качестве точки приложения вектора угловой скорости  может быть принята любая точка.
может быть принята любая точка.
Вектор углового ускорения  также лежит на оси вращения, совпадает по направлению с вектором угловой скорости
также лежит на оси вращения, совпадает по направлению с вектором угловой скорости  в случае ускоренного вращения
в случае ускоренного вращения 
Вопрос №12
В векторном виде формулу для линейной скорости можно написать как векторное произведение:

Вопрос №13
ац=w2×R направлено по радиусу к оси (центру) вращения
авр=e×r×sina направлено по касательной к траектории точки, т.е. параллельно скорости
Вопрос №14
Сложным движением называют такое движение, при котором точка участвуют в 2ух или более движениях.
1. Абсолютное (движение относительно неподвижной системы отсчета)
2. Относительное (движение относительно подвижной системы отсчета)
3. Переносное (движение подвижной системы отсчета относительно неподвижной)
Переносная скорость- скорость некоторой точки подвижной системы отсчета, с которой в данный момент совпадает точка М относительно неподвижной сист.
Относительная скорость- скорость точки относит подвижн сист отсч
Абсолютная скорость это скорость точки относительно неподвижной системы отсчета
Вопрос №15
Вопрос №16
Абсолютная скорость точки в сложном движении равна геометрической сумме относительной и переносной скоростей
 =
=  +
+ 
Вопрос №17
Вопрос №18
Абсолютное ускорение точки в сложном движении = геометрической сумме переносного, относительного и кориолисова ускорений.
 =
=  +
+  +
+ 
Вопрос №21
 =2(
=2(  x
x  )
)
Ускорение Кориолиса направлено перпендекулярно плоскости векторов w и vr в ту сторону, откуда виден поворот от w к vr на наименьший угол против хода часовой стрелки.
Правило Жуковского: проектируем вектор относительной скорости  на плоскость, перпендекулярную вектору переносной угловой скорости и переворачиваем эту проекцию в той же плоскости на угол 90 в сторону переносной угловой скорости.
на плоскость, перпендекулярную вектору переносной угловой скорости и переворачиваем эту проекцию в той же плоскости на угол 90 в сторону переносной угловой скорости.
Равенство 0 ускорения Кориолиса:
1. w= 0; переносное движение явл поступат
2.  =0; относит скорость в данный момент = 0
=0; относит скорость в данный момент = 0
3.  =0; вектор углов скорости переносного дв w параллелен вектору относительной скорости
=0; вектор углов скорости переносного дв w параллелен вектору относительной скорости 
Вопрос №22
Сферическое движение (движение твёрдого тела вокруг неподвижной точки) — движение абсолютно твёрдого тела, при котором оно имеет одну неподвижную точку.
При движении вокруг неподвижной точки О каждая из точек твёрдого тела описывает в пространстве сферическую поверхность, центром которой является точка О.
φ = f1(t) — угол собственного вращения;
ψ = f2(t) — угол прецессии;
θ = f1(t) — угол нутации.
Угловая скорость- это вектор направленный вдоль мгновенной оси вращения, модуль которого равен w= 
Вопрос №23
Движение свободного твердого тела состоит из поступательного движения совместно с полюсом и сферического движения вокруг полюса, которое не зависит от поступательного движения.
Уравнения движения:
| xA = xA(t),yA = yA(t), zA = zA(t), ψA = ψA(t), θA = θA(t), φA = φA(t) |
ψ, θ φ -углы Эйлера
Вопрос № 24
Плоским или плоскопараллельным движением твердого тела называется такое его движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости, например движение колеса вагона на прямолинейном участке пути, движение шатуна кривошипно-шатунного механизма.
Вместо плоского движения тела достаточно изучить движение плоской фигуры в ее плоскости.


Уравнения уравнениями плоского движения твердого тела.
Вопрос №25
Всякое перемещение плоской фигуры в ее плоскости можно представить как совокупность двух перемещений: 1) поступательного перемещения, зависящего от выбора полюса; 2) вращательного перемещения вокруг полюса; угол и направление поворота от выбора полюса не зависят.
Вопрос №26
Пусть в момент времени  фигура занимала положение
фигура занимала положение  (рис. 2.17), а в момент времени
(рис. 2.17), а в момент времени 
 - положение
- положение  . Переместим сначала фигуру поступательно в положение
. Переместим сначала фигуру поступательно в положение  а затем повернем ее на угол
а затем повернем ее на угол  вокруг точки
вокруг точки  . Заметим, что поступательное перемещение зависит от выбора полюса, а угол поворота не зависит от него. Действительно, тот же переход из положения
. Заметим, что поступательное перемещение зависит от выбора полюса, а угол поворота не зависит от него. Действительно, тот же переход из положения  в положение
в положение  можно осуществить, приняв за полюс точку
можно осуществить, приняв за полюс точку  и переместив сначала фигуру в положение
и переместив сначала фигуру в положение  (причем все точки фигуры получат перемещения, геометрически равные
(причем все точки фигуры получат перемещения, геометрически равные  и отличные от
и отличные от  , а затем повернув фигуру на
, а затем повернув фигуру на  вокруг точки
вокруг точки 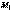 .
.
Но углы  , так как отрезки
, так как отрезки  и
и  параллельны и повороты вокруг точек
параллельны и повороты вокруг точек 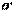 и
и  происходят в одну сторону.
происходят в одну сторону.
Продифференцировав равенство, получим 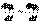 ;
;  ,
,
т. е. угловая скорость и угловое ускорение не зависят от выбора полюса плоской фигуры при плоском ее движении.
Вопрос №27
Теорема о сложении скоростей – скорость любой точки плоской фигуры равна геометрической сумме скоростей полюса и вращательной скорости этой точки вокруг полюса.
Следствие 1 Проекции скоростей точек плоской фигуры на ось, проходящую через эти точки равны .
Следствие 2 Концы векторов скоростей точек плоской фигуры, лежащих на одной прямой, также лежат на одной прямой и делят эту прямую на отрезки пропорциональные расстояниям между точками.
Вопрос №28
Мгнове́нный центр скоросте́й — при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело.
Теорема:
Если тело в плоском движении имеет угловую скорость, то мгновенный центр скоростей существует.
Вопрос №29
Для определения положения мгновенного центра скоростей необходимо провести перпендикуляры к прямым, параллельным линейным скоростям выбранных точек тела. В точке пересечения этих перпендикуляров и будет находиться мгновенный центр скоростей.
Существуют особые случаи нахождения мгновенного центра скоростей

Вопрос №31
Определение скоростей точек плоской фигуры можно выполнить одним их следующих методов:
- аналитическим;
- основанным на использовании векторного уравнения;
- основанным на использовании теоремы о проекциях скоростей точек тела на прямую, проходящую через эти точки;
- основанным на использовании мгновенного центра скоростей.
Наиболее часто применяется последний метод.
Вопрос №32
Вопрос №33
Определение ускорений можно выполнить одним из следующих методов:
- аналитическим;
- основанным на использовании векторного уравнения;
- основанным на использовании мгновенного центра ускорений.
Дата добавления: 2015-04-15; просмотров: 258; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Кинематика. Какая из приведенных ниже формул выражает понятие скорости: |