
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Необходимые теоретические сведения.
Решение матричных уравнений
Методические указания для проведения упражнений
по курсу аналитической геометрии
Калуга 2011г.
Содержание.
Цели занятия стр.4
План занятия стр.4
Необходимые теоретические сведения стр.5
Практическая часть стр.6
Контроль освоения пройденного материала стр.10
Домашнее задание стр.11
Количество часов: 2
Цели занятия:
1. Систематизировать полученные теоретические знания о видах матричных уравнений и способах их решения.
2. Применить на практике методы решения матричных уравнений.
План занятия:
1. Кратко изложить теоретический материал.
2. Решить матричное уравнение вида  методом с использованием обратной матрицы.
методом с использованием обратной матрицы.
3. Решить матричное уравнение вида  методом, основанным на элементарных преобразованиях строк матрицы.
методом, основанным на элементарных преобразованиях строк матрицы.
4. Сравнить использованные методы.
5. Решить матричное уравнение вида  методом с использованием обратной матрицы.
методом с использованием обратной матрицы.
6. Решить матричное уравнение вида 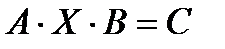 методом с использованием обратной матрицы.
методом с использованием обратной матрицы.
7. Проверить выполнение текущего домашнего задания.
8. Провести проверочную работу.
9. Представить тему следующего семинарского занятия.
10. Выдать текущее домашнее задание.
Необходимые теоретические сведения.
Рассмотрим два вида матричных уравнений относительно неизвестной матрицы  :
:  и
и  , где матрицы
, где матрицы 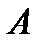 и
и  - известны, причем
- известны, причем  - квадратная и невырожденная.
- квадратная и невырожденная.
Опр. Некоторую матрицу называют решением матричного уравнения относительно неизвестной матрицы  , если при ее подстановке вместо
, если при ее подстановке вместо  матричное уравнение превращается в тождество.
матричное уравнение превращается в тождество.
Дата добавления: 2015-04-15; просмотров: 202; Мы поможем в написании вашей работы!; Нарушение авторских прав |