
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Если для матриц и существуют обратные матрицы и соответст
Если для матриц  и
и  существуют обратные матрицы
существуют обратные матрицы  и
и  соответственно, умножим обе части уравнения слева на
соответственно, умножим обе части уравнения слева на  , справа на
, справа на  . В результате получим:
. В результате получим:
 . Учитывая, что
. Учитывая, что 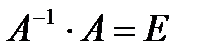 ,
, 
(  - единичная матрица) можно записать:
- единичная матрица) можно записать:  . Так как
. Так как
 - единичная матрица, окончательно имеем уравнение:
- единичная матрица, окончательно имеем уравнение:

где матрица  - решение уравнения.
- решение уравнения.
Если же хотя бы одна из матриц  или
или  не имеет обратную, уравнение не имеет решения.
не имеет обратную, уравнение не имеет решения.
Для матрицы  найдем
найдем  или докажем, что она не существует.
или докажем, что она не существует.
а)  обратная матрица существует.
обратная матрица существует.
б)  .
.
в) Найдем алгебраические дополнения для матрицы  и составим из них присоединенную матрицу
и составим из них присоединенную матрицу  :
:
 .
.
г) Известно, что  ; тогда
; тогда
 .
.
Для матрицы  найдем
найдем  или докажем, что она не существует.
или докажем, что она не существует.
а)  обратная матрица существует.
обратная матрица существует.
б)  .
.
в) Найдем алгебраические дополнения для матрицы  и составим из них присоединенную матрицу
и составим из них присоединенную матрицу  :
:
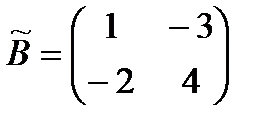 .
.
г) По формуле  ;
;
 .
.
Найдем неизвестную матрицу  .
.

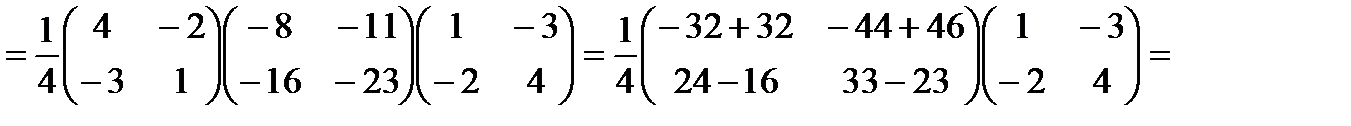
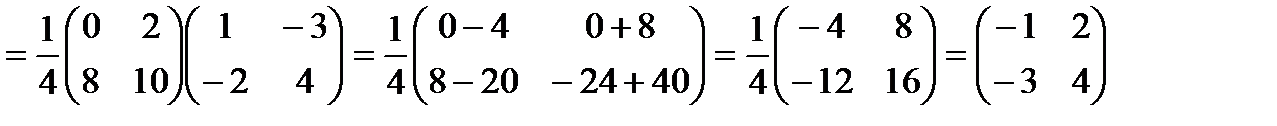 .
.
Дата добавления: 2015-04-15; просмотров: 209; Мы поможем в написании вашей работы!; Нарушение авторских прав |