
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематика материальной точки
Кинематика представляет собой раздел механики, изучающий формальные характеристики движения независимо от причин, вызывающих движение. Модельным объектами кинематики, как и всей механики, являются материальная точка и абсолютно твердое тело. В данном разделе рассмотрена кинематика материальной точки.
Положение частицы в пространстве характеризуется радиус-вектором  . Изменение положения частицы характеризуется вектором перемещения
. Изменение положения частицы характеризуется вектором перемещения  . Первая и вторая производные радиус-вектора по времени представляют собой соответственно скорость и ускорение. Во всех приводимых формулах точка означает дифференцирование по времени.
. Первая и вторая производные радиус-вектора по времени представляют собой соответственно скорость и ускорение. Во всех приводимых формулах точка означает дифференцирование по времени.
 (1.1)
(1.1)
 (1.2)
(1.2)
Линия, по которой движется тело, называется траекторией. Длина траектории представляет собой путь (s). Путь – скалярная величина. Производная пути по времени представляет собой абсолютную величину скорости
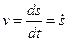 (1.3)
(1.3)
Вектор ускорения материальной точки может быть разложен на составляющие, направленные вдоль траектории и перпендикулярно ей. Эти составляющие называются соответственно тангенциальным ( 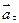 ) и нормальным (
) и нормальным ( 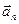 ) ускорениями.
) ускорениями.
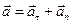 (1.4)
(1.4)
Тангенциальное ускорение отвечает за изменение абсолютной величины скорости Его значение (в смысле проекции вектора ускорения на единичный вектор, касательный к траектории) находятся по формуле
 (1.5)
(1.5)
Нормальное ускорение отвечает за изменение направления вектора скорости. Его значение находится по формуле
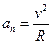 (1.6)
(1.6)
где R – радиус кривизны траектории в соответствующей точке. Под радиусом кривизны следует понимать радиус окружности, которая аппроксимирует истинную траекторию на ее малом участке. Центр этой окружности называется центром кривизны траектории в данной точке.
При движении по окружности радиуса R положение точки на ней задается углом поворота j. Первая и вторая производные угла поворота по времени представляют собой соответственно угловую скорость w и угловое ускорение b. Связь между линейной и угловой скоростью дается выражением
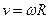 (1.7)
(1.7)
Формула (1.7) может использоваться и при движении по произвольной траектории, если под R понимать радиус кривизны.
ЗАДАЧИ
1. Покоившееся в начале координат тело в момент времени t = 0 начинает двигаться с ускорением 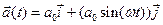 Найти: а). Закон движения тела
Найти: а). Закон движения тела  ; б). Зависимость величины тангенциального ускорения от времени.
; б). Зависимость величины тангенциального ускорения от времени.
Ответ: 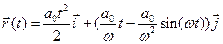 ;
; 
2. Скорость частицы задана формулами 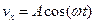 ,
, 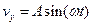 ,
,  , где A и B – константы. Найти величины нормального, тангенциального и полного ускорений.
, где A и B – константы. Найти величины нормального, тангенциального и полного ускорений.
Ответ:  ;
; 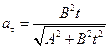 ;
; 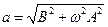
3. Координаты тела при движении в плоскости меняются по закону 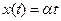 ;
; 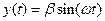 , где a, b, w - константы. Как изменяются со временем величины полного, тангенциального и нормального ускорений и мгновенный радиус кривизны траектории тела? Найти и нарисовать траекторию движения тела.
, где a, b, w - константы. Как изменяются со временем величины полного, тангенциального и нормального ускорений и мгновенный радиус кривизны траектории тела? Найти и нарисовать траекторию движения тела.
Ответ: 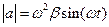 ;
; 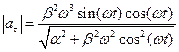 ;
; 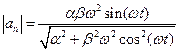 ;
;  ;
; 
15. Скорость частицы задана формулами: 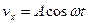 ,
, 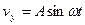 ,
,  . Найти тангенциальное, нормальное и полное ускорения.
. Найти тангенциальное, нормальное и полное ускорения.
Ответ: 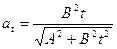 ,
, 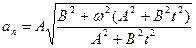 ,
, 
16. Тело движется по окружности радиуса R с угловой скоростью 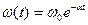 . Как зависит от времени модуль вектора ускорения?
. Как зависит от времени модуль вектора ускорения?
Ответ: 
17. Тело движется в плоскости по закону  ;
; 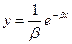 , a, b - константы. Найти зависимость нормального ускорения тела от времени
, a, b - константы. Найти зависимость нормального ускорения тела от времени
Ответ: 
18. В момент времени t = 0 тело начинает вращаться по окружности радиуса R с угловой скоростью, зависящей от времени по закону 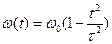 , где w0 и t - константы. Найти: 1). путь, пройденный телом до остановки; 2). зависимость модуля полного ускорения тела от времени.
, где w0 и t - константы. Найти: 1). путь, пройденный телом до остановки; 2). зависимость модуля полного ускорения тела от времени.
Ответ: 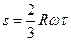 ,
, 
19. Тело брошено со скоростью v0 под углом a к горизонту. Найти нормальное и тангенциальное ускорения и радиус кривизны траектории в трех точках: начальной, верхней и конечной. Сопротивлением воздуха пренебречь.
Ответ: начальная и конечная точки (модули):  ,
, 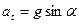 ,
, 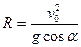 .
.
Верхняя точка:  ,
, 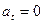 ;
; 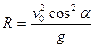
9. Одна из частиц пылевого облака (точка A) покоится, а остальные разлетаются от нее со скоростями, определяемыми выражением 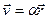 (a = const,
(a = const,  – радиус-вектор, проведенный из точки A). Какую картину обнаружит наблюдатель, движущийся вместе с точкой B?
– радиус-вектор, проведенный из точки A). Какую картину обнаружит наблюдатель, движущийся вместе с точкой B?
Ответ: Все частицы разлетаются радиально от точки В.
10. Мальчик плывет со скоростью, в два раза меньшей скорости течения реки. В каком направлении к другому берегу он должен плыть, чтобы его снесло течением как можно меньше?
Ответ: 30° от направления перпендикуляра к берегам
11. Частица движется горизонтально со скоростью v0 и попадает в зону ширины L (расположенную вдоль направления движения частицы), где ей сообшается постоянное вертикальное ускорение a0. С какой скоростью и под каким углом к горизонтали частица покинет зону?
Ответ:  ;
; 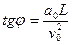
12. Тело начинает двигаться из точки A и движется сначала равноускоренно в течение времени t0, затем с тем же по модулю ускорением – равнозамедленно. Через какое время от начала движения тело вернется в точку А?
Ответ: 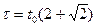
13. Тело движется вдоль оси х, его скорость меняется по закону v(t) = v0cos(2pt/T). Найти путь, пройденный телом за время от T/8 до T/4.
Ответ: 
14. Закон движения точки обода колеса, катящегося равномерно по горизонтальному пути (ось X), имеет вид  ,
,  . Найти: а). путь, пройденный точкой А между двумя последовательными касаниями полотна дороги; б). модуль и направление ускорения точки А.
. Найти: а). путь, пройденный точкой А между двумя последовательными касаниями полотна дороги; б). модуль и направление ускорения точки А.
Ответ: s = 8b; a = bw2 (к центру колеса)
15. Пассажир первого вагона поезда длины L прогуливался по перрону. Когда он был рядом с последним вагоном, поезд начал двигаться с ускорением a. Пассажир сразу же побежал со скоростью v. Через какое время он догонит свой вагон?
Ответ: 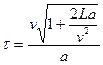
16. Тело движется из начала координат, замедляясь по прямой с ускорением, модуль которого зависит от скорости как 
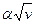 , где a = const. В начальный момент времени скорость равна v0. Где остановится тело?
, где a = const. В начальный момент времени скорость равна v0. Где остановится тело?
Ответ: 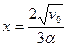
17. Воздушный шар поднимается вверх с постоянной скоростью v0 и сносится ветром. Скорость ветра зависит от высоты по закону vx = ay, где a > 0. Найти уравнение траектории шара и зависимости нормального, тангенциального и полного ускорений от высоты.
Ответ: 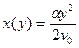 ,
, 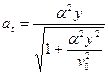 ,
,  ,
, 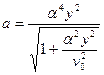
18. Точка движется в плоскости ХУ по закону  ,
, 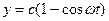 , где с и w - положительные постоянные. Найти путь, проходимый точкой за время t.
, где с и w - положительные постоянные. Найти путь, проходимый точкой за время t.
Ответ: 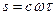
19. Частица движется в положительном направлении оси X так, что ее скорость меняется по закону 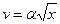 , где a > 0. Пусть при t = 0 x = 0. Найти зависимость от времени скорости и ускорения частицы.
, где a > 0. Пусть при t = 0 x = 0. Найти зависимость от времени скорости и ускорения частицы.
Ответ: 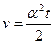 ,
, 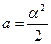
20.  Собака бежит равномерно со скоростью v так, что вектор скорости все время нацелен на лису, которая в свою очередь бежит прямолинейно и равномерно со скоростью u < v. В начальный момент времени
Собака бежит равномерно со скоростью v так, что вектор скорости все время нацелен на лису, которая в свою очередь бежит прямолинейно и равномерно со скоростью u < v. В начальный момент времени 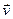 ^
^ 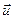 и расстояние между собакой и лисой равно L. Через какое время собака догонит лису?
и расстояние между собакой и лисой равно L. Через какое время собака догонит лису?
Ответ: 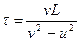
21. В сферической лунке прыгает шарик, упруго ударяясь о стенки в двух точках, расположенных на одной горизонтали. Промежуток времени между двумя столкновениями при движении слева направо равен T1, а при движении справа налево – T2. Определить радиус лунки.
Ответ: 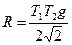
22. Один конец раздвижной штанги закреплен на ободе колеса радиуса R, а второй шарнирно закреплен на расстоянии 2R от центра колеса. Колесо вращается с постоянной угловой скоростью w. Найти амплитуду качания штанги и два полупериода ее движения.
Ответ: 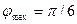 ,
, 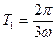 ,
, 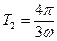
23. Радиус-вектор материальной точки меняется по закону  . Найти величину тангенциальной составляющей ускорения.
. Найти величину тангенциальной составляющей ускорения.
Ответ: 
24. Модуль скорости частицы меняется со временем по закону 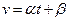 , где a и β – положительные постоянные. Модуль ускорения частицы равен 3a. Найти тангенциальное и нормальное ускорения в зависимости от времени.
, где a и β – положительные постоянные. Модуль ускорения частицы равен 3a. Найти тангенциальное и нормальное ускорения в зависимости от времени.
Ответ: 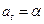 ,
, 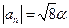
25. Идет отвесный дождь. Скорость капель равна u. По асфальту со скоростью v скользит мяч. Во сколько раз за один и тот же промежуток времени на него попадет больше капель, чем на неподвижный мяч?
Ответ: 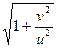
26. Скорость течения реки зависит от расстояния до берега квадратично по закону 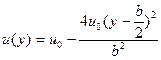 , где y – расстояние до берега, b – ширина реки, u0 – скорость в середине реки. Гребец гребет перпендикулярно берегу, скорость лодки относительно воды равна v. Найти снос лодки.
, где y – расстояние до берега, b – ширина реки, u0 – скорость в середине реки. Гребец гребет перпендикулярно берегу, скорость лодки относительно воды равна v. Найти снос лодки.
Ответ: 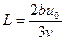
27. Кот Леопольд сидел у края крыши сарая. Вредный мышонок выстрелил в него из рогатки. Вектор начальной скорости камня был направлен точно на кота. Однако камень, описав дугу, упал у основания сарая через время t. Чему равна высота сарая?
 Ответ:
Ответ: 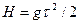
28. Три жука находятся в вершинах равностороннего треугольника со стороной a. Они начинают одновременно ползти с постоянной по модулю скоростью v так, что первый жук все время держит курс на второго, второй – на третьего, третий – на первого. Через какое время жуки встретятся?
Ответ: 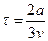
29. Двигатели космического корабля, движущегося со скоростью v0, включаются на торможение, создавая ускорение 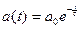 , и не выключаются. Каким должен быть параметр t, чтобы корабль остановился? Каков при этом будет его тормозной путь?
, и не выключаются. Каким должен быть параметр t, чтобы корабль остановился? Каков при этом будет его тормозной путь?
Ответ: 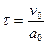 ,
, 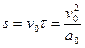
30. Подводная лодка, погружающаяся вертикально и равномерно, испускает звуковые импульсы длительностью t0. Длительность импульса, отраженного от дна, равна t. Скорость звука с. Найти скорость лодки.
Ответ: 
31. Из полусферического аквариума радиуса R, наполненного водой, с единицы поверхности воды в единицу времени испаряется объем жидкости q. Через какое время вся вода испарится?
Ответ: 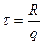
32. Тело налетает на стенку со скоростью v под углом a к линии, перпендикулярной стенке. Стенка движется со скоростью w перпендикулярно самой себе навстречу телу. Определить в лабораторной системе отсчета модуль скорости тела после упругого удара о стенку. При ударе скорость стенки не меняется.
Ответ: 
33. Дымовая шашка падает вертикально с высоты H с нулевой начальной скоростью. Дым сносится ветром, который дует горизонтально на всех высотах с постоянной скоростью v0. На какое расстояние будет снесен дым относительно вертикальной траектории шашки на высоте h от поверхности Земли в момент падения шашки на Землю?
Ответ: 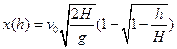
Дата добавления: 2015-04-15; просмотров: 1386; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| График выполнения и сдачи заданий (СРС) по дисциплине | | | Концепция субъективной ценности |