Кинематический анализ исходного звена

Для анализа необходимы следующие исходные данные: число оборотов кривошипа в минуту (n=650 об/мин), длина кривошипа (O₁А = 80 мм = 0,08м).

Требуется определить скорость V_A и ускорение W_A точки А.

Число оборотов и угловая скорость связаны соотношением:

(1.3)

Скорость точки А

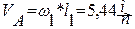(1.4)

направлена перпендикулярно к звену O₁А в сторону его вращения.

Полное ускорение точки А, кривошипа 1, состоит только из нормальной составляющей, т.к. угловая скорость кривошипа принята постоянной определяем:

(1.5)

1.4. Построение планов скоростей для 2-х положений механизма.

Построение начинаем с выбора масштабного коэффициента плана скоростей:

μ_v=V_A/πa , (1.4)

где πa -отрезок, который будет изображать на плане скоростей скорость V_A

μ_v=0,125

Выбираем полюс плана скоростей произвольную точку p. Проводим из точки p перпендикулярно кривошипу OA₁ прямую, на которой откладываем вектор длиной paв сторону вращения кривошипа. Для определение скорости ползуна, точки В можно записать следующие векторное уравнение:

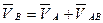(1.5)

где V_А - скорость точки А, направлена по касательной к траектории движения кривошипа, перпендикулярно ОА; V_AB- скорость движения точки B относительно А, направлена перпендикулярно звену АВ. Таким образом, чтобы построить V_В, надо из конца вектора pa провести перпендикуляр к AВ до пересечения с линией движения ползуна (проведенной через полюс). Полученный вектор πb и будет вектором скорости точки B.

Для определения положения скорости центра масс звена 2 запишем соотношение:

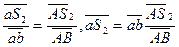(1.6)

Отложив от точки a плана скоростей отрезок на линии 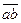и соединив точку с полюсом плана скоростей, получим вектор скорости точки , а натуральная величина найдется как:

= , (1.7)

а натуральную величину скорости точки В:

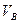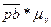= . (1.8)

1.5. Построение планов ускорений для 2-х положения механизма.

Построение плана ускорений рассмотрим на примере 1 положения механизма. Для определения ускорения точки B запишем векторное уравнение [1]:

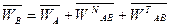(1.9)

где W_A -ускорение точки А кривошипа;

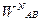-нормальное ускорение звена АВ; определяем как 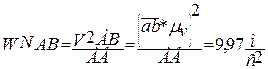, (1.10)

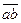-отрезок с плана скоростей;

АВ – расстояние между точками А и В, м.

-тангенциальное ускорение звена АВ.

Выбираем полюсное расстояние p, от полюса откладываем отрезок pWa который будет равен ускорению точки А кривошипа 1 (в известном нам направлении, от точки вращение А к центру вращения 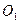). Определяем масштабный коэффициент [1]:

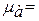5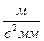

Из конца Wα проводим вектор 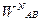в предварительно выбранном масштабе, из его конца проводим линию действия вектора , которая перпендикулярна линии действии предыдущего вектора. Ее проводим до пересечения с линией действия ускорения ползуна, которая проходит через полюс р. Точка пересечения этих двух направлений определяет величины и направления векторов и 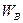, оба они направлены стрелками к этой точке. Соединив отрезком прямой точки конца векторов и , и направив его в сторона конца вектора , получим вектор полного ускорения 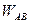. Натуральные величины найдем используя масштабный коэффициент:

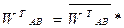
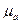; (1.11)

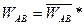
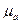; (1.12)

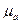; (1.13)

Для определения положения ускорения центра масс звена 2 запишем соотношение:

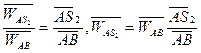(1.14)

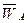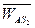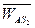Отложив от точки плана ускорений отрезок на линии действия вектора и соединив точку с полюсом плана скоростей, получим вектор ускорения точки , а натуральная величина найдется как:

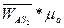(1.15)

РАЗДЕЛ 2. Силовой расчет механизма.

Проектирование нового механизма всегда включает его силовое исследование, так как по найденным силам производится последующий расчет на прочность элементов кинематических пар и звеньев механизма.

При силовом исследовании решаются следующие основные задачи а)определяются силы, действующие на звенья и реакции в кинематических парах,

б)определяется уравновешивающая сила (момент силы).

При силовом анализе дополнительно выясняют вопросы об урав­новешенности механизма, износе его звеньев, о потерях на трение в отдельных кинематических парах, о коэффициенте полезного действия механизма в целом и др.

В курсовом проекте силовой расчет ведется методом кинетостатики. Метод кинетостатики основан на принципе Даламбера, который применительно к механизмам можно сформулировать так: если ко всем внешним силам, действующим на систему звеньев, добавить силы инерции, тогда под действием всех этих сил система звеньев может условно считаться находящейся в равновесии.

При кинетостатическом расчете кинематическую цепь механизма разбиваем на группы Ассура, которые являются статически определимыми. Расчет ведем путем последовательного рассмотрения условий равновесия отдельно каждой группы, начиная с наиболее удаленной от исходного механизма, последним рассчитывается ведущее звено.

Определение реакций в кинематических парах механизма ведем без учета трения методом планов сил при постоянной угловой скорости кривошипа.

2.1. Силовой расчет кинематической пары звеньев 2-3.

Силовой расчет механизма ведем для положения 1, к которому построен план ускорений. Зарисовываем группу в масштабе μ_l=0,001 м/мм, сохраняя положения звеньев, прикладывая Р_пс=0Н. Прикладываем также, силы веса

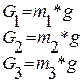, (2.1)

где 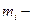масса звена, кг

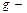ускорение свободного падения, ,

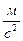силы инерции:

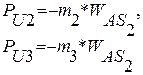(2.2)

со стороны отброшенных звеньев в поступательной паре прикладываем неизвестную реакцию перпендикулярно направляющей ползуна и в шарнире А прикладываем также неизвестную реакцию 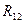, которую можно разложить на составляющие согласно равенству:

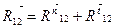, (2.3)

где 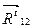направляется перпендикулярно линии звена АВ, а 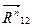параллельна этой линии.
Определяем тангенциальную составляющую 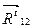, составляя уравнение звена 2 в форме моментов относительно точки В:

(2.4)

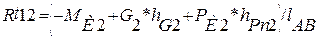, (2.5)

где 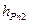-плечо силы 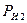, равное μ_l* ,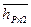

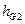- плечо силы веса, равное 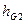= μ_l* ,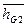

-момент силы инерции, Н*м,

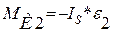, (2.6)

где 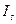- момент инерции относительно центра масс S звена 2,

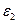- угловое ускорение звена, ;

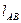- длина звена 2.

Точное направление определиться знаком полученного результата , при отрицательном результате направление следует принять за противоположное.

Для того, чтоб определить 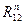и , запишем уравнение равновесия все группы в векторной форме:

(2.7)

Векторы сил, известные по величине и направлению, подчеркнуты двумя чертами, известные только по направлению линии действия одной, в данном случае это силы 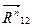и .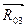

Для построения плана сил определяем масштабный коэффициент плана сил 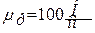, а отрезки, выражающие векторы сил на плане, получаются делением натуральных значений сил на плане на масштаб на плане. Размещая векторы 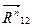и 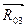радом, находим точку их пересечения, которая определяет величины этих векторов и их точные направления, а соединив начало 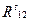с концом 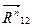, определяем вектор 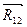полной реакции в шарнире А.

2.2 Силовой расчет ведущего звена.

Зарисовываем звено в масштабе μ_l=0,002м/мм, прикладывая в точку А

известную реакцию 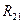(которая равна и противоположна по направлению 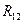). Уравновешивающую силу прикладываем в точке А перпендикулярно звено , ее плечом будет длина кривошипа. Освобождаем звено от связей со стойкой и прикладываем вместо нее реакцию .

Запишем векторное уравнение сил, действующих на ведущее звено:

(2.9)

Из всех сил действующих на кривошип, неизвестными являются величина 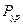и величина и направление реакции . На кривошип также действует сила веса 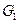в центре масс 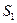, который совпадает с точкой . Уравновешивающую силу 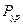целесообразно определить из уравнения равновесия кривошипа в форме моментов относительно точки

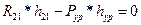(2.10)

где ,

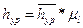
Решая уравнение (2.11) относительно 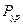получаем

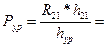7742 Н,

Решая уравнения (2.9) строим план сил, в предварительно выбранном масштабе и определим из него вектор искомой реакции . По правилу сложения векторов этот вектор направлен к началу .

ЗАКЛЮЧЕНИЕ

При выполнении первого раздела курсового проекта был проведен кинематический анализ механизма методом планов. Во втором разделе рассмотрены построение планов сил, действующих на звенья реакции в кинематических парах, определена уравновешивающая сила методом планов.

СПИСОК ЛИТЕРАТУРЫ

1. Проектирование и кинематика плоских механизмов. Учебное пособие. Составители: Н.Н. Федоров., Издательство ОмГТУ, Омск 2000, 144 с.

2. Кинетостатика плоских механизмов и динамика машин. Учебное пособие. Составители: Н.Н. Федоров., Издательство ОмГТУ, Омск 2000, 144 с.

3. Артоболевский И. И. Теория механизмов и машин. Учебник для вузов - М.: Наука, 1988, 640 с.